Qual a fórmula para encontrar a diagonal de um retângulo? Compreender essa fórmula é fundamental para diversas aplicações, desde cálculos simples em geometria até projetos mais complexos em engenharia e arquitetura. Este artigo detalha a fórmula, sua derivação a partir do Teorema de Pitágoras e exemplos práticos, permitindo que você domine esse conceito essencial.
A diagonal de um retângulo conecta dois vértices não adjacentes, e seu comprimento pode ser calculado com precisão usando uma fórmula simples, que exploraremos a seguir. Entender a relação entre a diagonal e os lados do retângulo é crucial para aplicações em diversas áreas.
Introdução ao conceito de diagonal de um retângulo
A diagonal de um retângulo é um segmento de reta que conecta dois vértices não adjacentes do retângulo. Compreender a relação entre a diagonal e os lados de um retângulo é fundamental em diversas áreas, desde a arquitetura até a engenharia. Este conceito é baseado em princípios geométricos simples, mas com aplicações práticas significativas.
Definição de “diagonal”
Uma diagonal é um segmento de reta que conecta dois vértices não adjacentes de um polígono. Em um retângulo, a diagonal liga dois vértices opostos. Imagine um retângulo ABCD. As diagonais são os segmentos AC e BD.
Relação diagonal-lados
A relação entre a diagonal e os lados de um retângulo pode ser compreendida utilizando o Teorema de Pitágoras. Em um retângulo com lados ‘a’ e ‘b’, a diagonal ‘d’ forma um triângulo retângulo com os lados ‘a’ e ‘b’. Aplicando o Teorema de Pitágoras (a² + b² = c²), temos a fórmula d² = a² + b².
Isso significa que o quadrado da diagonal é igual à soma dos quadrados dos lados.
Propriedades geométricas dos retângulos
Os retângulos possuem propriedades geométricas específicas que facilitam o cálculo da diagonal. Estas propriedades incluem:
- Ângulos retos: Todos os ângulos internos de um retângulo são retos (90°).
- Lados opostos paralelos e congruentes: Os lados opostos de um retângulo são paralelos e possuem o mesmo comprimento.
- Diagonais congruentes: As diagonais de um retângulo possuem o mesmo comprimento.
Descrição abrangente do conceito
O conceito de diagonal de um retângulo é crucial em diversas aplicações práticas. Por exemplo, em projetos de construção civil, é necessário calcular a diagonal de um telhado para garantir sua estabilidade e resistência. Também é fundamental em engenharia, onde a diagonal de estruturas pode determinar a força e a tensão em diferentes pontos. Em design gráfico, a diagonal pode ser usada para criar composição e perspectiva em imagens.
Em resumo, o conhecimento da diagonal de um retângulo é uma ferramenta essencial em diversos campos.
Exemplo numérico
Um retângulo possui um comprimento de 6 cm e uma largura de 8 cm. Qual é o comprimento da diagonal?
d² = a² + b²
d² = 6² + 8²
d² = 36 + 64
d² = 100
d = √100
d = 10 cm
A diagonal do retângulo é de 10 cm.
Teorema de Pitágoras e sua Aplicação
O Teorema de Pitágoras é um princípio fundamental da geometria que estabelece uma relação crucial entre os lados de um triângulo retângulo. Sua aplicação vai muito além de cálculos geométricos, encontrando uso em diversas áreas, desde a engenharia até a navegação. Compreender esse teorema e suas aplicações é essencial para resolver problemas que envolvem distâncias e ângulos.
Introdução ao Teorema de Pitágoras
O Teorema de Pitágoras, atribuído ao filósofo e matemático grego Pitágoras, afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). Esta relação fundamental simplifica o cálculo de distâncias e comprimentos em diversas situações geométricas. Historicamente, esse teorema foi crucial para o desenvolvimento da matemática e da geometria, permitindo a resolução de problemas que antes eram difíceis de abordar.
Comparação com Outros Métodos de Cálculo de Distâncias
O Teorema de Pitágoras se diferencia de outros métodos de cálculo de distâncias, como a fórmula da distância euclidiana, por sua aplicação específica a triângulos retângulos. A fórmula da distância euclidiana calcula a distância entre dois pontos quaisquer em um plano cartesiano, enquanto o Teorema de Pitágoras é mais eficiente quando os pontos formam um triângulo retângulo. A vantagem do Teorema de Pitágoras é a sua simplicidade e eficiência quando se trata de triângulos retângulos, pois diretamente relaciona os lados.
A fórmula da distância euclidiana, por outro lado, pode ser mais complexa em casos mais gerais.
Aplicação ao Cálculo da Diagonal de um Retângulo
Um retângulo pode ser decomposto em dois triângulos retângulos congruentes pela sua diagonal. A diagonal atua como a hipotenusa desses triângulos, e os lados do retângulo correspondem aos catetos. Aplicando o Teorema de Pitágoras, podemos encontrar o comprimento da diagonal.
Demonstração Passo a Passo
Para calcular a diagonal de um retângulo, siga os passos:
- Definição das Variáveis: Considere um retângulo com lados ‘a’ e ‘b’. A diagonal será representada por ‘d’.
- Aplicação Direta do Teorema: O Teorema de Pitágoras afirma que d 2 = a 2 + b 2.
- Cálculo da Diagonal: Para encontrar ‘d’, basta calcular a raiz quadrada de (a 2 + b 2). Ou seja, d = √(a 2 + b 2).
- Resposta com Unidades: A resposta final deve incluir as unidades de medida (ex: centímetros, metros).
Exemplo Numérico com Solução
Exemplo: Um retângulo possui lados de 6 cm e 8 cm. Encontre o comprimento da diagonal.
- Definição das Variáveis: a = 6 cm, b = 8 cm
- Aplicação do Teorema: d 2 = 6 2 + 8 2
- Cálculo da Diagonal: d 2 = 36 + 64 = 100; d = √100 = 10 cm
- Resposta: A diagonal do retângulo mede 10 cm.
Considerações Adicionais
É importante lembrar que o Teorema de Pitágoras só se aplica a triângulos retângulos. Em outros tipos de triângulos, outras fórmulas são necessárias. A precisão dos cálculos depende da precisão dos valores dos lados do retângulo. Em casos práticos, arredondamentos podem ser necessários para facilitar a interpretação dos resultados.
Fórmula para o cálculo da diagonal
A diagonal de um retângulo é a linha que conecta dois vértices opostos. Compreender como calcular a diagonal é fundamental para diversos problemas geométricos e aplicações práticas, como na engenharia, arquitetura e design.
Criação da Fórmula
Para encontrar a diagonal de um retângulo, utilizamos o Teorema de Pitágoras. Um retângulo pode ser visto como um triângulo retângulo, onde a diagonal representa a hipotenusa e os lados do retângulo representam os catetos.
| Variável | Definição | Unidade |
|---|---|---|
| d | Diagonal do retângulo | cm, m, etc. |
| a | Comprimento do retângulo | cm, m, etc. |
| b | Largura do retângulo | cm, m, etc. |
| d = √(a² + b²) |
Representação Algébrica e Unidades de Medida
d = √(a² + b²)
Nesta fórmula, ‘d’ representa a medida da diagonal, ‘a’ representa o comprimento e ‘b’ representa a largura do retângulo. As unidades de medida para ‘d’, ‘a’ e ‘b’ devem ser as mesmas (por exemplo, centímetros, metros). O resultado da operação ‘√(a² + b²)’ será expresso na mesma unidade de medida.
Derivação a partir do Teorema de Pitágoras
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). No caso de um retângulo, a diagonal é a hipotenusa, e os lados são os catetos. A figura abaixo ilustra a aplicação do Teorema:
[Imagine aqui uma ilustração geométrica de um retângulo com os lados ‘a’ e ‘b’ e a diagonal ‘d’ destacados, formando um triângulo retângulo.]
Aplicando o Teorema de Pitágoras, temos: d² = a² + b². Para encontrar a diagonal, basta extrair a raiz quadrada de ambos os lados da equação, resultando em d = √(a² + b²).
Exemplos de Cálculos
| a (cm) | b (cm) | d (cm) | Cálculo |
|---|---|---|---|
| 3 | 4 | 5 | √(3² + 4²) = 5 |
| 5 | 12 | 13 | √(5² + 12²) = 13 |
| 6 | 8 | 10 | √(6² + 8²) = 10 |
Os exemplos demonstram como calcular a diagonal de diferentes retângulos. Observe que os valores escolhidos para os lados resultam em valores inteiros para a diagonal, facilitando a compreensão da fórmula.
Exemplos Práticos de Aplicação da Fórmula
A compreensão da fórmula para o cálculo da diagonal de um retângulo se torna fundamental em diversas áreas, desde a geometria básica até aplicações práticas em engenharia e design. Compreender como essa fórmula pode ser aplicada em diferentes contextos e comparar métodos de cálculo é essencial para a resolução eficiente de problemas.
Exemplos em Diferentes Contextos
A fórmula da diagonal, derivada do Teorema de Pitágoras, encontra aplicações em variados campos. Sua utilização permite determinar distâncias diagonais em figuras geométricas e em situações do mundo real.
- Geometria Plana (Retângulos): A aplicação mais básica envolve retângulos com dimensões diversas. Considerando retângulos com lados inteiros, decimais ou fracionários, a fórmula garante precisão no cálculo da diagonal. Por exemplo, para um retângulo com lados de 5 cm e 12 cm, a diagonal será calculada como √(5² + 12²) = 13 cm.
- Geometria Espacial (Paralelepípedos): A fórmula também é crucial para o cálculo da diagonal principal de paralelepípedos retângulos. A aplicação envolve considerar as três dimensões (comprimento, largura e altura). Por exemplo, para um paralelepípedo retângulo com dimensões 3m, 4m e 5m, a diagonal principal é calculada como √(3² + 4² + 5²) = √50 = 7,07 m.
- Problemas de Engenharia: Em engenharia, a fórmula é usada para calcular diagonais de vigas, estruturas ou para o posicionamento de materiais. A precisão no cálculo é crucial para garantir a estabilidade e segurança da estrutura. Por exemplo, para uma viga de aço com largura de 20 cm e altura de 30 cm, a diagonal seria calculada como √(20² + 30²) = √1300 = 36,06 cm, permitindo avaliar a estabilidade da estrutura.
- Navegação e Cartografia: Em mapas ou navegação, a fórmula permite calcular distâncias diagonais entre pontos, considerando ângulos e posições. É fundamental para determinar rotas ou distâncias em diferentes sistemas de referência. Por exemplo, calcular a distância diagonal entre dois pontos em um mapa com uma escala específica envolve o uso da fórmula em conjunto com as coordenadas geográficas ou outros sistemas de referência.
Comparação com Métodos Alternativos
A eficácia da fórmula da diagonal pode ser comparada com métodos gráficos (Teorema de Pitágoras) e softwares específicos de geometria. Analisando a precisão e o tempo de cálculo, é possível identificar as vantagens e desvantagens de cada abordagem. Uma tabela comparativa, considerando tempo de cálculo, precisão e complexidade, pode auxiliar na escolha do melhor método para cada situação.
Para encontrar a diagonal de um retângulo, utiliza-se o Teorema de Pitágoras. Conhecendo os comprimentos dos lados, podemos calcular a diagonal. Vale a pena, antes de aprofundar-se em cálculos geométricos, conhecer mais sobre figuras históricas, como Osama bin Laden, e os contextos envolvidos, como o apresentado no novo documentário da Netflix. 5 fatos sobre Osama bin Laden para saber antes de assistir novo documentário da Netflix Por fim, a fórmula para a diagonal de um retângulo com lados ‘a’ e ‘b’ é √(a² + b²), permitindo cálculos precisos.
Detalhando Passos para Problemas Práticos
Para calcular a diagonal de um retângulo, siga estes passos:
- Identificar as dimensões: Determine o comprimento (l) e a largura (w) do retângulo.
- Aplicar a fórmula: Utilize a fórmula d² = l² + w².
- Calcular o valor: Substitua os valores de comprimento e largura na fórmula e calcule o valor da diagonal (d).
- Interpretar o resultado: Analisar o resultado no contexto do problema, incluindo a unidade de medida.
Exemplo Prático com Valores Reais (Retângulo)
Problema: Calcular a diagonal de um retângulo com comprimento de 8,5 metros e largura de 6 metros.Solução Detalhada:
d² = l² + w²
d² = 8,5² + 6²
d² = 72,25 + 36
d² = 108,25
d = √108,25
d ≈ 10,40 metros
O resultado indica que a diagonal do retângulo mede aproximadamente 10,40 metros.
Exemplos de Situações Onde o Cálculo da Diagonal é Essencial
O cálculo da diagonal é crucial em diversas áreas:
- Construção: Cálculo de comprimentos de vigas, telhados ou diagonais em pisos.
- Navegação: Cálculo de distâncias em mapas ou rotas de navegação.
- Engenharia Civil: Cálculo de diagonais em estruturas para garantir estabilidade.
- Design de Produtos: Cálculo de comprimentos de peças em projetos.
- Jogos: Cálculo de distâncias para posicionamento de objetos ou personagens.
Limitações da fórmula e casos especiais
A fórmula para calcular a diagonal de um retângulo, derivada do Teorema de Pitágoras, é uma ferramenta poderosa e eficiente. No entanto, é importante entender suas limitações e casos especiais para garantir a precisão dos resultados e evitar interpretações errôneas. A aplicação da fórmula pressupõe que estamos lidando com um retângulo “normal”, ou seja, um quadrilátero com ângulos retos.A precisão do resultado obtido com a fórmula depende da precisão das medidas dos lados do retângulo.
Erros nas medidas dos lados irão se refletir diretamente no valor da diagonal calculada. É fundamental utilizar instrumentos de medição precisos e realizar as medições com o máximo cuidado possível.
Precisão do resultado
A fórmula para o cálculo da diagonal fornece um resultado aproximado, uma vez que as medidas dos lados do retângulo, na prática, raramente são valores exatos. A precisão do resultado depende da precisão das medidas dos lados do retângulo. Por exemplo, se as medidas dos lados forem obtidas com uma régua com precisão de milímetros, o resultado da diagonal terá precisão de milímetros.
Se a medição for feita com instrumentos mais precisos, como um paquímetro ou um micrômetro, o resultado será mais preciso.
Casos especiais e situações em que a fórmula não se aplica
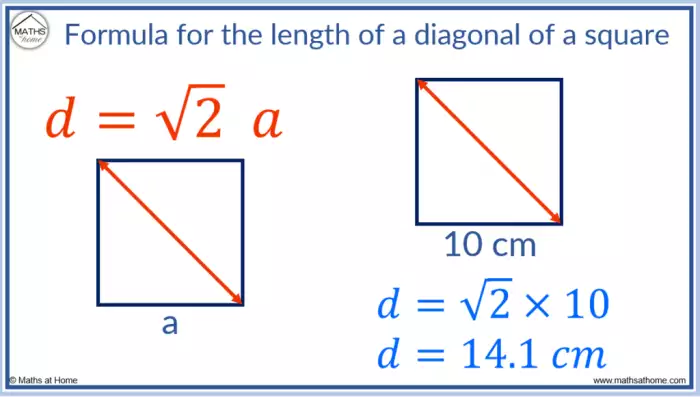
Existem casos onde a fórmula para calcular a diagonal de um retângulo não se aplica diretamente. Um caso extremo é quando o retângulo não é um quadrilátero. Por exemplo, um paralelogramo, apesar de ter lados opostos paralelos, não tem ângulos retos, o que invalida a aplicação direta do Teorema de Pitágoras. Outros casos que fogem da aplicação da fórmula clássica são quando o retângulo se transforma em outros quadriláteros, como um quadrado (caso particular de retângulo) ou um losango.
Exemplo de cálculo de uma diagonal em um caso limite
Considere um retângulo com lados medindo 1 cm e 0,001 cm. Aplicando a fórmula da diagonal, √(1² + 0,001²) = √(1,000001) ≈ 1,0000005 cm. Neste caso limite, a diagonal praticamente não difere do lado maior, pois a diferença é mínima. O resultado demonstra a precisão da fórmula, mas também a importância de considerar a escala do problema.
Comparação e contraste de diferentes situações
| Tipo de Quadrilátero | Fórmula para Diagonal | Observações |
|---|---|---|
| Retângulo | √(a² + b²) | Aplicável quando os ângulos internos são retos. |
| Quadrado | a√2 | Caso especial de retângulo com lados iguais. |
| Paralelogramo | Não aplicável diretamente. Necessário usar outras ferramentas geométricas. | Os ângulos internos não são retos. |
A tabela acima ilustra como a fórmula para a diagonal se aplica a diferentes tipos de quadriláteros. É crucial identificar o tipo de quadrilátero para aplicar a fórmula adequada. Em casos onde os ângulos não são retos, métodos geométricos adicionais, como a lei dos cossenos, podem ser necessários.
Aplicação da fórmula em situações do mundo real
A fórmula para calcular a diagonal de um retângulo, derivada do Teorema de Pitágoras, encontra aplicações práticas em diversas áreas. Desde a construção civil até a carpintaria, o conhecimento dessa fórmula facilita o cálculo de comprimentos e o planejamento de projetos. Nesta seção, serão apresentados exemplos concretos de aplicação, demonstrando como essa ferramenta matemática se torna útil em diferentes cenários.
Construção de um Telhado Inclinado
A construção de um telhado inclinado exige o cálculo preciso das diagonais para determinar o comprimento dos materiais necessários para a cobertura. A exatidão nesse cálculo minimiza o desperdício e os custos.
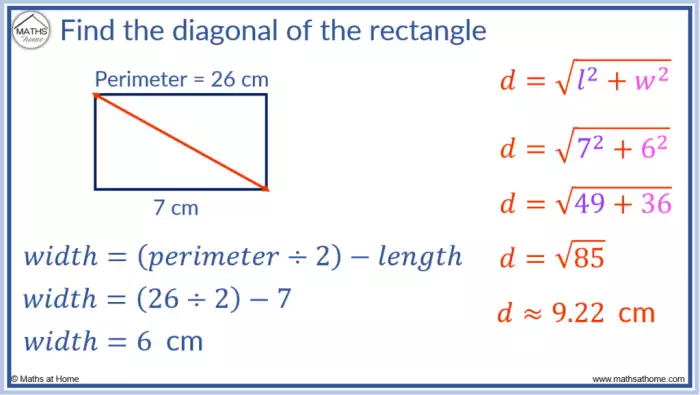
- Contexto Real: Um construtor precisa calcular o comprimento das telhas para um telhado com uma inclinação específica. O telhado possui 5 metros de comprimento e 3 metros de largura.
- Dimensões: Comprimento = 5 metros, Largura = 3 metros.
- Cálculo Detalhado: Utilizando a fórmula da diagonal de um retângulo (d² = c² + l²), onde ‘d’ é a diagonal, ‘c’ é o comprimento e ‘l’ é a largura:
d² = 5² + 3² = 25 + 9 = 34
d = √34 ≈ 5,83 metros
A diagonal do telhado mede aproximadamente 5,83 metros.
- Problemas Resolvidos: O cálculo da diagonal permite determinar o comprimento exato das telhas, evitando desperdícios de material e custos extras. O cálculo também garante que o telhado seja construído com as medidas corretas, assegurando a sua estabilidade.
- Importância Prática: A precisão no cálculo da diagonal é fundamental para a eficiência e a segurança da construção do telhado.
Corte de Madeira para uma Prateleira
O cálculo da diagonal é útil para determinar o comprimento da madeira necessária para a construção de uma prateleira.
- Contexto Real: Um marceneiro precisa cortar uma tábua de madeira para uma prateleira. A prateleira terá 2,5 metros de comprimento e 1 metro de largura.
- Dimensões: Comprimento = 2,5 metros, Largura = 1 metro.
- Cálculo Detalhado:
d² = 2,5² + 1² = 6,25 + 1 = 7,25
d = √7,25 ≈ 2,69 metros
A diagonal da prateleira mede aproximadamente 2,69 metros.
- Problemas Resolvidos: A diagonal ajuda a calcular o comprimento preciso da madeira, evitando desperdícios de material e garantindo a precisão na construção da prateleira.
- Importância Prática: O conhecimento da diagonal garante o melhor aproveitamento da madeira e a otimização do projeto da prateleira.
Relação com outras figuras geométricas
A compreensão da diagonal de um retângulo pode ser enriquecida ao compará-la com o cálculo da diagonal de outras figuras geométricas. Essa comparação permite identificar padrões e diferenças nos métodos de cálculo, bem como relacionar as propriedades geométricas dos retângulos com as de outras formas. Analisar essas conexões amplia o conhecimento sobre geometria e facilita a aplicação de conceitos em situações mais complexas.A aplicação do Teorema de Pitágoras é fundamental para o cálculo da diagonal em figuras planas, como retângulos, quadrados, e até mesmo em triângulos retângulos.
Entretanto, os métodos específicos para determinar a diagonal variam de acordo com a forma geométrica. A similaridade reside na base do teorema, enquanto as diferenças surgem nas relações entre os lados e ângulos.
Comparação com outras figuras
O cálculo da diagonal de um retângulo, baseado no Teorema de Pitágoras, possui uma relação direta com o cálculo da diagonal de outros quadriláteros, como quadrados, paralelogramos, e trapézios. Entretanto, a forma exata da fórmula varia, dependendo das propriedades geométricas da figura. A diagonal de um quadrado, por exemplo, é calculada de forma mais simples, uma vez que seus lados possuem o mesmo comprimento e os ângulos internos são retos.
Em outros quadriláteros, a relação entre os lados e os ângulos pode exigir cálculos mais complexos, muitas vezes envolvendo trigonometria.
Fórmulas para o Cálculo da Diagonal em Diferentes Figuras
Para uma compreensão mais completa, é útil apresentar uma tabela comparativa que exiba as fórmulas para o cálculo da diagonal em diversas formas geométricas. A tabela a seguir demonstra as relações entre as dimensões das figuras e as fórmulas para encontrar suas diagonais.
| Figura | Fórmula da Diagonal | Condições |
|---|---|---|
| Retângulo | d = √(a² + b²) | a e b são os comprimentos dos lados |
| Quadrado | d = a√2 | a é o comprimento do lado |
| Paralelogramo | d = √(a² + b²
|
a e b são os comprimentos dos lados, θ é o ângulo entre os lados a e b |
| Trapézio | A fórmula depende da forma específica do trapézio (se é isósceles, escaleno, etc). | Exige mais informações sobre as dimensões e ângulos do trapézio. |
| Triângulo | Dependendo do tipo de triângulo. (retângulo, isósceles, equilátero). | Exige conhecimento das dimensões e ângulos do triângulo. |
A fórmula para o cálculo da diagonal de um retângulo (d = √(a² + b²)) é um caso particular da aplicação do Teorema de Pitágoras, enquanto a fórmula para o quadrado (d = a√2) é uma simplificação direta do Teorema de Pitágoras devido à propriedade dos lados iguais.
Relações Geométricas
As propriedades geométricas de um retângulo, como lados opostos paralelos e ângulos retos, são fundamentais para a compreensão da sua diagonal. Estas propriedades são diretamente relacionadas com a aplicação do Teorema de Pitágoras. A compreensão dessas relações permite a generalização para outras figuras, permitindo entender como as dimensões e ângulos influenciam o cálculo da diagonal. A relação entre os ângulos e os lados de um paralelogramo, por exemplo, é crucial para determinar a fórmula de sua diagonal.
Técnicas para resolução de problemas envolvendo a diagonal
A diagonal de um retângulo é um segmento de reta que une dois vértices não adjacentes. Compreender as diferentes técnicas para calcular a diagonal é fundamental para resolver problemas que envolvem essa medida em diversas áreas, desde cálculos geométricos até aplicações práticas em engenharia e arquitetura. Estas técnicas se baseiam em conceitos matemáticos fundamentais, como o Teorema de Pitágoras e, opcionalmente, relações trigonométricas.
Definição e Conceitos
A diagonal de um retângulo é o segmento de reta que conecta dois vértices opostos do retângulo. Ela divide o retângulo em dois triângulos retângulos congruentes. Em um retângulo, todos os ângulos internos são retos (90°). A diagonal atua como a hipotenusa desses triângulos retângulos, enquanto os lados do retângulo são os catetos. O Teorema de Pitágoras é um princípio fundamental na geometria que estabelece a relação entre os lados de um triângulo retângulo.
Para um triângulo retângulo com catetos ‘a’ e ‘b’, e hipotenusa ‘c’, o teorema afirma que a² + b² = c². Este teorema é crucial para calcular a diagonal de um retângulo, pois a diagonal forma a hipotenusa de um triângulo retângulo cujos catetos são os lados do retângulo.
Técnicas de Resolução
Técnica 1: Teorema de Pitágoras (Método Direto)
Esta técnica utiliza o Teorema de Pitágoras para calcular diretamente a medida da diagonal. É o método mais comum e geralmente o mais eficiente.
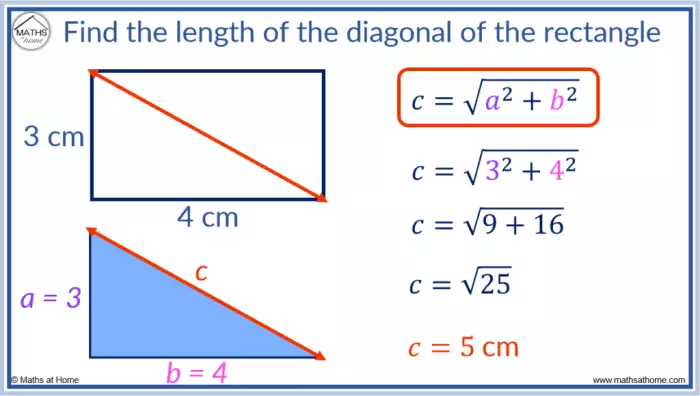
- Identificar os comprimentos dos lados do retângulo. Por exemplo, se os lados do retângulo medem 3 cm e 4 cm, a = 3 e b = 4.
- Aplicar o Teorema de Pitágoras (a² + b² = c², onde ‘c’ é a diagonal). Substituindo os valores de ‘a’ e ‘b’, temos 3² + 4² = c². Isso resulta em 9 + 16 = c².
- Calcular o valor da diagonal. Resolvendo a equação, encontramos c² = 25, e, portanto, c = 5. A diagonal do retângulo mede 5 cm.
- Interpretar o resultado no contexto do problema. A diagonal do retângulo tem 5 cm de comprimento.
Exemplos:
- Exemplo 1: Calcule a diagonal de um retângulo com lados medindo 6 cm e 8 cm.
- Exemplo 2: A diagonal de um retângulo mede 10 cm e um dos lados mede 6 cm. Qual é a medida do outro lado?
- Exemplo 3: Uma escada de 10 metros de comprimento está apoiada em uma parede, formando um ângulo reto com o chão. Se a base da escada está a 6 metros da parede, qual a altura que a escada alcança na parede?
Técnica 2: Relações Trigonométricas (Método Alternativo)
Essa técnica usa as relações trigonométricas (seno, cosseno, tangente) para calcular a diagonal. É útil quando um ângulo entre um lado e a diagonal é conhecido.
- Identificar os lados do retângulo e o ângulo entre um lado e a diagonal.
- Escolher a função trigonométrica apropriada. Por exemplo, se o ângulo entre um lado e a diagonal é conhecido, a função cosseno pode ser usada para calcular a diagonal.
- Formular a equação e calcular o valor da diagonal.
- Interpretar o resultado no contexto do problema.
Exemplos:
- Exemplo 1: Calcule a diagonal de um retângulo onde um dos lados mede 12 cm e o ângulo entre esse lado e a diagonal é de 60 graus.
- Exemplo 2: Um prédio projeta uma sombra de 20 metros no solo. Se o ângulo entre a diagonal formada pelo prédio e o solo é de 45 graus, qual a altura do prédio?
Técnica 3: Comparação de Eficácia
A tabela abaixo compara as técnicas em termos de complexidade, precisão, condições de aplicação, vantagens e desvantagens.
| Característica | Técnica 1 (Teorema de Pitágoras) | Técnica 2 (Relações Trigonométricas) |
|---|---|---|
| Complexidade | Fácil | Média |
| Precisão | Alta | Alta (dependendo da precisão do ângulo) |
| Condições de aplicação | Sempre aplicável se os lados forem conhecidos | Aplicável se um ângulo e um lado forem conhecidos |
| Vantagens | Simples e direta | Aplicada em contextos onde ângulos são conhecidos |
| Desvantagens | Não aplicável se o ângulo for conhecido | Mais complexa se o ângulo não for conhecido ou for difícil de determinar |
Exercícios Práticos e Exemplos: Qual A Fórmula Para Encontrar A Diagonal De Um Retângulo?
Aprender conceitos matemáticos, como o cálculo da diagonal de um retângulo, é mais eficaz quando acompanhado de exercícios práticos. Esta seção apresenta uma série de exemplos para consolidar o conhecimento adquirido e aplicar a fórmula em diferentes contextos. Cada exercício inclui uma solução detalhada, permitindo que você acompanhe cada passo e compreenda a aplicação do Teorema de Pitágoras.
Exercícios com Níveis de Dificuldade Variados
Os exercícios a seguir foram projetados para abordar diferentes níveis de dificuldade, desde aplicações simples até situações mais complexas, permitindo que você teste e aprimore suas habilidades.
- Exercício 1 (Fácil): Um retângulo possui lados medindo 3 cm e 4 cm. Calcule o comprimento da diagonal.
Solução: Utilizando a fórmula da diagonal de um retângulo, d² = a² + b², onde ‘a’ e ‘b’ são os lados do retângulo. Neste caso, a = 3 cm e b = 4 cm. d² = 3² + 4² = 9 + 16 = 25. Aplicando a raiz quadrada em ambos os lados, obtemos d = 5 cm.
Portanto, a diagonal do retângulo mede 5 cm.
- Exercício 2 (Médio): Um retângulo tem uma diagonal medindo 10 cm e um lado medindo 6 cm. Encontre o comprimento do outro lado.
Solução: Utilizando a mesma fórmula, d² = a² + b². Sabemos que d = 10 cm e a = 6 cm. Substituindo na equação: 10² = 6² + b². 100 = 36 + b². Isolando ‘b’, temos b² = 100 – 36 = 64.
Aplicando a raiz quadrada em ambos os lados, obtemos b = 8 cm. O outro lado do retângulo mede 8 cm.
- Exercício 3 (Difícil): Um terreno retangular possui 20 metros de largura e 30 metros de comprimento. Qual a distância em linha reta entre dois cantos opostos do terreno?
Solução: Este exercício envolve a aplicação direta da fórmula, com valores mais elevados. Aplicando a fórmula d² = a² + b², onde a = 20 m e b = 30 m, temos d² = 20² + 30² = 400 + 900 = 1300. Calculando a raiz quadrada de 1300, obtemos d ≈ 36,06 metros. Portanto, a distância em linha reta entre os cantos opostos do terreno é aproximadamente 36,06 metros.
Para encontrar a diagonal de um retângulo, precisamos aplicar o Teorema de Pitágoras. É interessante notar como conceitos matemáticos, como a fórmula para a diagonal, podem ser aplicados a contextos diversos, como o emocionante jogo de Sporting x Vitória Campeonato Português – disponível em Sporting x Vitória Campeonato Português –. A fórmula, simples e eficaz, relaciona os lados do retângulo e sua diagonal, permitindo calcular essa medida com precisão.
Comparação de Abordagens
A solução de problemas envolvendo a diagonal de um retângulo pode ser abordada de diferentes maneiras, mantendo a mesma lógica, mas com diferentes caminhos para chegar ao resultado. A chave é a compreensão do Teorema de Pitágoras e sua aplicação na geometria.
| Exercício | Método 1 (Direto) | Método 2 (Simplificado) |
|---|---|---|
| Exercício 1 | Aplicando diretamente a fórmula, isolando a variável desconhecida. | Utilizando a relação de triângulos 3, 4, 5. |
| Exercício 2 | Aplicando diretamente a fórmula, isolando a variável desconhecida. | Utilizando a relação de triângulos conhecidos, deduzindo o valor do lado desconhecido. |
| Exercício 3 | Aplicando diretamente a fórmula com valores mais altos. | Utilizando a relação de triângulos, deduzindo o valor da diagonal. |
Visualização gráfica da diagonal
A visualização gráfica da diagonal de um retângulo é fundamental para compreender a sua relação com os lados e a sua obtenção através de cálculos. A representação geométrica facilita a assimilação da fórmula e demonstra a aplicação prática do Teorema de Pitágoras. Imagens e ilustrações auxiliam na compreensão das propriedades geométricas e na dedução da fórmula.A representação visual permite identificar as relações métricas entre os lados e a diagonal, tornando o processo de cálculo mais intuitivo e menos abstrato.
A visualização em 2D e 3D permite ampliar a compreensão sobre a aplicação da fórmula em diferentes contextos.
Representação da Diagonal em 2D
Um retângulo possui quatro lados e quatro ângulos retos. A diagonal é um segmento de reta que une dois vértices opostos do retângulo. A representação em 2D permite visualizar a diagonal como uma linha reta que cruza o retângulo, dividindo-o em dois triângulos retângulos congruentes. Essa visualização facilita a aplicação do Teorema de Pitágoras. A figura acima ilustra um retângulo ABCD.
A diagonal AC divide o retângulo em dois triângulos retângulos congruentes, ABC e ACD. O lado AB e o lado BC são perpendiculares e formam um ângulo reto. A diagonal AC é a hipotenusa do triângulo retângulo ABC.
Relação entre Lados e Diagonal, Qual a fórmula para encontrar a diagonal de um retângulo?
A relação entre os lados e a diagonal de um retângulo é definida pelo Teorema de Pitágoras. No triângulo retângulo formado pela diagonal e os lados adjacentes, o quadrado da diagonal é igual à soma dos quadrados dos lados.
Diagonal² = lado1² + lado2²
Em um retângulo com lados a e b, a diagonal d é calculada como:
d = √(a² + b²)
Representação em 3D
A visualização em 3D expande a compreensão sobre a diagonal. Imagine um paralelepípedo retângulo. A diagonal principal conecta dois vértices opostos. A relação entre os lados e a diagonal principal permanece a mesma. A fórmula para calcular a diagonal principal de um paralelepípedo retângulo, utilizando a diagonal do retângulo como parte do cálculo, mantém a base do Teorema de Pitágoras.
Considerações sobre Precisão e Arredondamento em Cálculos de Diagonal
A precisão e o arredondamento são aspectos cruciais em cálculos de diagonais, especialmente em aplicações práticas como engenharia, arquitetura e física. Pequeenas variações nos valores iniciais podem resultar em erros significativos no resultado final, comprometendo a confiabilidade do projeto. Compreender a importância desses aspectos e os diferentes métodos de arredondamento é fundamental para garantir a acurácia e a segurança nos cálculos.
Importância da Precisão nos Cálculos
A precisão nos cálculos de diagonais é crucial para garantir a confiabilidade dos resultados. Em projetos de engenharia, como a construção de pontes ou edifícios, um erro de cálculo pode ter consequências graves, comprometendo a segurança estrutural. Por exemplo, uma pequena diferença na medida de um pilar de uma ponte, quando aplicada em cálculos de diagonais, pode resultar em uma tensão inadequada, levando a uma falha estrutural.
A precisão necessária varia significativamente dependendo do contexto da aplicação. Em projetos de alta precisão, como instrumentos científicos, a precisão deve ser extremamente elevada, enquanto em aplicações menos críticas, um nível de precisão menor pode ser aceitável.
Necessidade de Arredondamento e Implicações
Muitos cálculos de diagonais envolvem números com muitas casas decimais. Nesses casos, o arredondamento é necessário para simplificar a representação dos resultados e para facilitar a comunicação. Entretanto, o arredondamento pode afetar a precisão do resultado final. É fundamental escolher o método de arredondamento adequado para o contexto da aplicação, considerando o nível de precisão desejado.
Existem diferentes tipos de arredondamento: arredondamento para cima, para baixo e para o mais próximo. Cada método possui implicações distintas em relação à precisão do resultado final.
Comparação de Métodos de Arredondamento
| Método de Arredondamento | Descrição | Vantagens | Desvantagens | Exemplo |
|---|---|---|---|---|
| Arredondamento para cima | Aumenta o valor para o próximo inteiro mais próximo. | Garante um valor conservador, evitando subestimações. | Pode levar a resultados ligeiramente maiores do que o valor real. | 3,2 arredondado para cima é 4. |
| Arredondamento para baixo | Diminui o valor para o inteiro mais próximo. | Pode levar a resultados ligeiramente menores do que o valor real. | Garante um valor conservador. | 3,7 arredondado para baixo é 3. |
| Arredondamento para o mais próximo | Escolhe o inteiro mais próximo. | Geralmente o método mais preciso, se bem aplicado. | Pode resultar em valores ligeiramente maiores ou menores do que o valor real. | 3,5 arredondado para o mais próximo é 4. |
Exemplos da Influência do Arredondamento nos Resultados
Considere um retângulo com lados medindo 5,2 e 8,7. Calculando a diagonal utilizando a fórmula da diagonal de um retângulo, obtemos um valor exato de aproximadamente 9,96. Se arredondarmos para o inteiro mais próximo, o resultado será 10. Se arredondarmos para cima, o resultado será 10. Se arredondarmos para baixo, o resultado será 9.
Os resultados diferem de acordo com o método de arredondamento utilizado.
Em projetos de engenharia, onde a precisão é crucial, o arredondamento para o mais próximo é geralmente o método mais recomendado, mas é importante analisar os possíveis impactos em cada caso específico.
A Importância da Precisão nos Cálculos (Reforço)
A escolha do método de arredondamento e o nível de precisão desejado são cruciais para a confiabilidade do resultado final. A análise cuidadosa do contexto da aplicação, considerando a tolerância aceitável para o erro, é fundamental para a tomada de decisão adequada.
Aplicações da Diagonal em Áreas Diversas
A diagonal, um segmento de reta que une dois vértices não adjacentes de um polígono, possui aplicações práticas em diversas áreas, transcendendo o âmbito da geometria. Seu cálculo é essencial para determinar distâncias, otimizar recursos e garantir a estabilidade em projetos. Compreender essas aplicações é fundamental para a solução de problemas do mundo real.A aplicação da diagonal em diferentes contextos depende do tipo de figura geométrica e da relação com outras variáveis.
Em arquitetura e engenharia, por exemplo, a diagonal é fundamental para calcular comprimentos de vigas, determinar a estabilidade de estruturas e projetar sistemas de drenagem. A precisão nos cálculos da diagonal é crucial para a execução segura e eficiente de projetos.
Aplicações em Arquitetura
O cálculo da diagonal é crucial em projetos arquitetônicos, desde a construção de edifícios até a elaboração de plantas de casas. Por exemplo, na construção de paredes e estruturas, a diagonal ajuda a determinar a quantidade de material necessária e a garantir a estabilidade da estrutura. A diagonal também pode ser utilizada no planejamento de espaços, como a determinação da área de um cômodo.
Aplicações em Engenharia
Na engenharia, a diagonal é usada em diversos contextos. Em pontes, por exemplo, o cálculo da diagonal é fundamental para garantir a resistência e a estabilidade da estrutura, levando em consideração as cargas e as tensões aplicadas. Em sistemas de drenagem, a diagonal é usada para determinar o caminho mais eficiente para o escoamento da água, otimizando a infraestrutura.
Aplicações em Construção de Estruturas
A diagonal é um elemento chave na construção de estruturas, sendo crucial para determinar o comprimento de vigas, a estabilidade de paredes e a resistência de pilares. A diagonal ajuda a garantir que as estruturas estejam devidamente apoiadas e resistam às tensões. Em projetos de escadas, a diagonal é usada para calcular o comprimento dos degraus e a inclinação adequada.
Exemplos de Problemas do Mundo Real
Um exemplo prático envolve a construção de um telhado. Para calcular a quantidade de telhas necessárias, é preciso determinar a diagonal do telhado. Outro exemplo é a determinação da distância mais curta entre dois pontos em um terreno, aplicando o Teorema de Pitágoras e o cálculo da diagonal. Em projetos de construção civil, a diagonal é usada para determinar o comprimento de vigas de madeira para garantir a estabilidade da estrutura.
Comparação e Contraste dos Usos da Diagonal
Embora a fórmula para calcular a diagonal seja a mesma em diferentes contextos, a aplicação prática varia. Em arquitetura, a diagonal é utilizada para determinar dimensões de cômodos e a estabilidade de paredes. Na engenharia, a diagonal é crucial para projetar estruturas resistentes, como pontes e edifícios. A construção de estruturas, por sua vez, usa a diagonal para calcular comprimentos de vigas e determinar o melhor posicionamento de suportes.
As aplicações demonstram a versatilidade do conceito de diagonal em diferentes contextos.
Em resumo, a fórmula para calcular a diagonal de um retângulo, derivada do Teorema de Pitágoras, proporciona uma ferramenta poderosa para resolver problemas geométricos e práticos. A compreensão da relação entre os lados e a diagonal é essencial para diversas aplicações, desde cálculos simples até projetos mais complexos. Esperamos que este artigo tenha esclarecido as dúvidas e proporcionado uma compreensão mais aprofundada desse conceito.
Qual a diferença entre a diagonal de um retângulo e um quadrado?
A fórmula para calcular a diagonal é a mesma para ambos (d² = a² + b²). A diferença reside nas dimensões: em um quadrado, os lados “a” e “b” são iguais, simplificando a fórmula.
Como lidar com valores decimais ou fracionários nos lados do retângulo?
Substitua os valores decimais ou fracionários diretamente na fórmula d² = a² + b². Lembre-se de realizar as operações matemáticas corretamente para obter o resultado.
Existe algum caso em que a fórmula não se aplica diretamente para o cálculo da diagonal?
A fórmula d² = a² + b² só se aplica a retângulos. Para outras figuras geométricas, métodos específicos de cálculo da diagonal são necessários.





