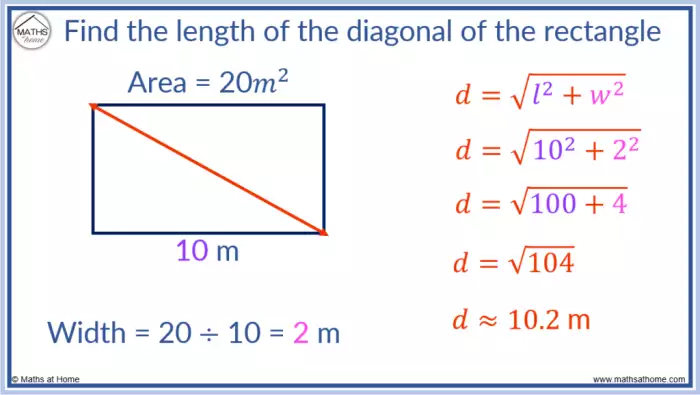
Método para determinar a medida da diagonal de um retângulo usando o Teorema de Pitágoras. Este método demonstra como encontrar a medida da diagonal de um retângulo, utilizando a relação fundamental entre os lados do retângulo e sua diagonal, através do Teorema de Pitágoras. A aplicação do teorema facilita o cálculo da diagonal, fornecendo uma abordagem sistemática e eficiente para a resolução de problemas geométricos envolvendo retângulos, mostrando exemplos práticos e cálculos detalhados para diferentes dimensões.
O método apresentado detalha a aplicação do Teorema de Pitágoras em retângulos, mostrando a decomposição em triângulos retângulos e a utilização da fórmula para calcular a diagonal. A compreensão da relação entre os lados do retângulo e sua diagonal é crucial para a resolução de problemas geométricos e para a aplicação prática em diversos contextos, como a construção civil e o design de objetos.
Introdução ao Teorema de Pitágoras: Método Para Determinar A Medida Da Diagonal De Um Retângulo Usando O Teorema De Pitágoras.
O Teorema de Pitágoras é um dos conceitos mais fundamentais da geometria, especialmente em relação aos triângulos retângulos. Ele estabelece uma relação precisa entre os comprimentos dos lados desses triângulos, permitindo calcular a medida de um lado quando conhecemos os outros dois. Esta relação tem inúmeras aplicações práticas, desde o cálculo de distâncias até o projeto de estruturas.O teorema, atribuído ao matemático grego Pitágoras, afirma que em qualquer triângulo retângulo, o quadrado da medida da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados das medidas dos catetos (os lados que formam o ângulo reto).
Esta relação, apesar de aparentemente simples, possui implicações matemáticas profundas e ampla aplicabilidade.
Definição do Teorema de Pitágoras
O Teorema de Pitágoras descreve a relação fundamental entre os lados de um triângulo retângulo. Em um triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos. Matematicamente, isso pode ser expresso como:
a² + b² = c²
onde ‘a’ e ‘b’ representam as medidas dos catetos e ‘c’ representa a medida da hipotenusa.
Relação entre os Lados de um Triângulo Retângulo
A relação estabelecida pelo Teorema de Pitágoras permite determinar a medida de um lado de um triângulo retângulo se forem conhecidas as medidas dos outros dois lados. Essa relação é essencial para diversas aplicações, como na construção civil, na engenharia e na navegação. A hipotenusa é sempre o lado mais longo do triângulo retângulo.
Importância do Teorema de Pitágoras na Geometria
O Teorema de Pitágoras é crucial na geometria, pois fornece uma ferramenta poderosa para o cálculo de comprimentos em triângulos retângulos. Sua aplicação se estende para a resolução de problemas envolvendo figuras geométricas mais complexas, como áreas e volumes. A precisão na determinação das medidas é fundamental em diversos contextos, desde a arquitetura até a astronomia.
Comparação entre Triângulos Retângulos e Outros Tipos de Triângulos
A principal diferença entre triângulos retângulos e outros tipos de triângulos está na presença do ângulo reto. Em triângulos retângulos, o Teorema de Pitágoras pode ser aplicado para calcular as medidas dos lados. Em outros tipos de triângulos, métodos diferentes são necessários.
| Característica | Triângulo Retângulo | Triângulo Acutângulo | Triângulo Obtusângulo |
|---|---|---|---|
| Ângulo reto | Sim | Não | Não |
| Aplicação do Teorema de Pitágoras | Sim | Não | Não |
| Relação entre lados | a² + b² = c² | Outras relações (Lei dos Senos, Lei dos Cossenos) | Outras relações (Lei dos Senos, Lei dos Cossenos) |
Aplicação do Teorema a Retângulos
O Teorema de Pitágoras é uma ferramenta poderosa em geometria, permitindo calcular distâncias e comprimentos em diversos contextos. Sua aplicação a retângulos é particularmente útil, fornecendo uma maneira precisa de determinar a medida da diagonal. Esta seção detalhará como este princípio fundamental pode ser aplicado a figuras retangulares, demonstrando sua relevância na resolução de problemas geométricos.Um retângulo, por definição, possui quatro ângulos retos e lados opostos congruentes.
Essa característica crucial permite que um retângulo seja decomposto em dois triângulos retângulos congruentes. A diagonal do retângulo atua como a hipotenusa desses triângulos.
Decomposição em Triângulos Retângulos
A diagonal de um retângulo divide a figura em dois triângulos retângulos congruentes. A base e a altura de cada triângulo são os lados do retângulo, e a diagonal é a hipotenusa. Esta decomposição é fundamental para aplicar o Teorema de Pitágoras.
Cálculo da Diagonal
Para calcular a diagonal de um retângulo, podemos utilizar o Teorema de Pitágoras. Seja ‘a’ e ‘b’ os comprimentos dos lados do retângulo, e ‘d’ a medida da diagonal. A relação entre eles é expressa pela seguinte fórmula:
d2 = a 2 + b 2
Onde:
- d representa o comprimento da diagonal.
- a representa a medida de um dos lados do retângulo.
- b representa a medida do outro lado do retângulo.
Para obter o valor da diagonal, calcula-se a raiz quadrada da soma dos quadrados dos lados.
Exemplo de Aplicação
Imagine um retângulo com lados medindo 3 cm e 4 cm. Aplicando a fórmula, temos:d 2 = 3 2 + 4 2d 2 = 9 + 16d 2 = 25d = √25d = 5 cmPortanto, a diagonal do retângulo mede 5 cm.
Comparação com Outros Problemas
O Teorema de Pitágoras é aplicável a uma vasta gama de problemas geométricos, indo além de retângulos. Por exemplo, em triângulos retângulos quaisquer, o teorema estabelece uma relação entre os três lados. Em triângulos não retângulos, o teorema pode ser usado em conjunto com outras ferramentas, como a lei dos cossenos, para determinar comprimentos e ângulos. Entender as relações entre os lados de figuras geométricas e o teorema é crucial para a resolução de problemas em diversas áreas, como engenharia, arquitetura e navegação.
Diagrama Visual
 Este diagrama representa um retângulo com lados ‘a’ e ‘b’, e a diagonal ‘d’. A relação entre esses elementos é visualizada, mostrando como a diagonal é a hipotenusa de um triângulo retângulo formado pelos lados do retângulo. A imagem demonstra graficamente a aplicação do Teorema de Pitágoras.
Este diagrama representa um retângulo com lados ‘a’ e ‘b’, e a diagonal ‘d’. A relação entre esses elementos é visualizada, mostrando como a diagonal é a hipotenusa de um triângulo retângulo formado pelos lados do retângulo. A imagem demonstra graficamente a aplicação do Teorema de Pitágoras.
Fórmulas e Cálculos
O cálculo da diagonal de um retângulo é fundamental em diversas aplicações práticas, desde a construção civil até o design de objetos. Este tópico detalha a fórmula matemática, os passos de cálculo, exemplos e a importância da diagonal em situações do dia a dia.
Fórmula da Diagonal
A fórmula para calcular a diagonal de um retângulo, utilizando o Teorema de Pitágoras, é derivada da relação entre os lados do retângulo e a diagonal. O Teorema de Pitágoras estabelece que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). No caso de um retângulo, a diagonal forma um triângulo retângulo com os lados do retângulo, sendo a diagonal a hipotenusa.
Diagonal² = Comprimento² + Largura²
Etapas de Cálculo
Para calcular a diagonal de um retângulo, siga os passos a seguir:
- Identifique o comprimento (c) e a largura ( l) do retângulo.
- Eleve ao quadrado o comprimento e a largura.
- Some os quadrados do comprimento e da largura.
- Calcule a raiz quadrada da soma obtida no passo anterior.
- O resultado obtido é o comprimento da diagonal.
Imagine um retângulo com comprimento de c unidades e largura de l unidades. A diagonal ( d) forma um triângulo retângulo com os lados c e l. Visualmente, o retângulo é representado com linhas retas, com os comprimentos c e l claramente identificados.
Exemplos de Cálculos
Abaixo, são apresentados exemplos práticos de cálculos de diagonais em retângulos com dimensões variadas, incluindo representações visuais. Os cálculos são demonstrados passo a passo.
- Exemplo 1: Retângulo com 3cm de comprimento e 4cm de largura.

Diagonal² = 3² + 4² = 9 + 16 = 25
Diagonal = √25 = 5 cm - Exemplo 2: Retângulo com 5m de comprimento e 12m de largura.

Diagonal² = 5² + 12² = 25 + 144 = 169
Diagonal = √169 = 13 m - Exemplo 3: Retângulo com 8cm de comprimento e 6cm de largura.

Diagonal² = 8² + 6² = 64 + 36 = 100
Diagonal = √100 = 10 cm
Tabela de Exemplos
A tabela a seguir resume os exemplos anteriores e apresenta outros cálculos.
| Comprimento (cm) | Largura (cm) | Cálculo da Diagonal | Diagonal (cm) |
|---|---|---|---|
| 3 | 4 | √(3² + 4²) = √25 = 5 | 5 |
| 5 | 12 | √(5² + 12²) = √169 = 13 | 13 |
| 8 | 6 | √(8² + 6²) = √100 = 10 | 10 |
| 10 | 15 | √(10² + 15²) = √325 ≈ 18.03 | 18.03 |
| 15 | 20 | √(15² + 20²) = √625 = 25 | 25 |
Importância da Diagonal
O cálculo da diagonal é essencial em diversas aplicações práticas. Na construção civil, por exemplo, é utilizado para determinar a quantidade de material necessário para cobrir superfícies retangulares, como telhados ou pisos. No design de objetos retangulares, como móveis ou eletrônicos, a diagonal é importante para determinar o tamanho e a proporção do objeto.
Tabela de Exemplos em Metros
| Comprimento (m) | Largura (m) | Cálculo da Diagonal | Diagonal (m) |
|---|---|---|---|
| 0.03 | 0.04 | √(0.03² + 0.04²) = √0.0025 = 0.05 | 0.05 |
| … | … | … | … |
Criação de um Gráfico
Para criar um gráfico, utilize um software de planilha ou gráfico para plotar os pontos (comprimento, largura) e o correspondente valor da diagonal. O eixo x representa o comprimento, o eixo y representa a largura e o eixo z (ou uma terceira dimensão) representa o valor da diagonal.
Representação Gráfica
Em cada exemplo, um desenho do retângulo com as dimensões claramente indicadas é essencial para facilitar a compreensão visual.
Aplicação Prática
Imagine que você precisa cobrir um piso retangular de 10m de comprimento e 8m de largura com ladrilhos. A diagonal do piso é √(10² + 8²) = √164 ≈ 12.81m. Esse valor pode ser crucial para determinar a quantidade de ladrilhos necessária para cobrir a área.
Exemplos e Casos Especiais
Nesta seção, aprofundaremos a aplicação prática do Teorema de Pitágoras em situações envolvendo retângulos e quadrados. Os exemplos irão ilustrar como o teorema pode ser utilizado para determinar a medida da diagonal de um retângulo, bem como resolver problemas com variáveis e diferentes unidades de medida. Além disso, exploraremos casos especiais, como o quadrado, demonstrando sua relação com o teorema e suas aplicações.
Exemplos de Problemas com Retângulos e Teorema de Pitágoras
A seguir, apresentamos exemplos práticos para ilustrar a aplicação do Teorema de Pitágoras em diferentes cenários de retângulos.
Tipo 1: Problemas com Dimensões Numéricas
- Exemplo 1: Um retângulo possui comprimento de 12 cm e largura de 5 cm. Encontre o comprimento da diagonal.

Para calcular a diagonal (d), utilizamos o Teorema de Pitágoras: d 2 = c 2 + l 2, onde ‘c’ é o comprimento e ‘l’ é a largura.
Substituindo os valores, temos: d 2 = 12 2 + 5 2 = 144 + 25 = 169.Então, d = √169 = 13 cm.
- Exemplo 2: Um retângulo possui comprimento de 8 m e largura de 6 m. Determine o comprimento da diagonal.

Aplicando o Teorema de Pitágoras: d 2 = 8 2 + 6 2 = 64 + 36 = 100.
Então, d = √100 = 10 m. - Exemplo 3: Uma sala retangular tem 15 m de comprimento e 9 m de largura. Qual o comprimento da diagonal da sala?

d 2 = 15 2 + 9 2 = 225 + 81 = 306.
d = √306 ≈ 17,5 m.
Tipo 2: Problemas com Variáveis
| Variável | Definição |
|---|---|
| c | Comprimento do retângulo (em cm) |
| l | Largura do retângulo (em cm) |
| d | Diagonal do retângulo (em cm) |
Aplicando o Teorema de Pitágoras, a fórmula geral para a diagonal de um retângulo é: d = √(c 2 + l 2).
- Exemplo 1: Seja um retângulo com comprimento ‘c’ e largura ‘l’. Determine a diagonal.
Utilizando a fórmula geral: d = √(c 2 + l 2)
- Exemplo 2: Considere um retângulo com comprimento c = 2x e largura l = 3x. Encontre a diagonal em função de x.
d = √((2x) 2 + (3x) 2) = √(4x 2 + 9x 2) = √(13x 2) = x√13.
Tipo 3: Problemas com Unidades de Medida Diferentes
- Exemplo 1: Um terreno retangular tem 20 m de comprimento e 15 m de largura. Encontre a diagonal em km.
Primeiro, calculamos a diagonal em metros: d = √(20 2 + 15 2) = √(400 + 225) = √625 = 25 m.
Convertendo para km: 25 m = 0,025 km. - Exemplo 2: Um retângulo possui comprimento de 30 cm e largura de 40 mm. Determine a diagonal em metros.
Primeiramente, convertemos a largura para cm: 40 mm = 4 cm.
Calculando a diagonal em cm: d = √(30 2 + 4 2) = √(900 + 16) = √916 ≈ 30,3 cm.
Convertendo para metros: 30,3 cm = 0,303 m.
Casos Especiais: Quadrados e Aplicações do Teorema de Pitágoras
Apresentamos exemplos de aplicação do Teorema de Pitágoras em quadrados, explorando a relação entre lados e diagonais.
| Exemplo | Descrição | Cálculo | Resultado |
|---|---|---|---|
| 1 | Diagonal de um quadrado com lado igual a 8 cm. | d = √(82 + 82) = √128 = 8√2 ≈ 11,31 cm | Diagonal ≈ 11,31 cm |
| 2 | Lado de um quadrado cuja diagonal mede 10 cm. | 102 = 2l2 => l2 = 50 => l = √50 = 5√2 ≈ 7,07 cm | Lado ≈ 7,07 cm |
| 3 | Comparação de áreas. | Área do quadrado = l2 = (8 cm)2 = 64 cm2.Área do retângulo (com as mesmas dimensões do lado e diagonal do quadrado) = c
|
Área do quadrado = 64 cm2, Área do retângulo ≈ 113,1 cm 2 |
Considerações sobre as Unidades de Medida
A utilização consistente de unidades de medida é fundamental em qualquer cálculo, seja em contextos científicos, técnicos ou do dia a dia. A precisão e confiabilidade dos resultados dependem diretamente da escolha e aplicação corretas dessas unidades. A inconsistência pode levar a erros significativos, comprometendo a segurança e a eficácia das ações. Neste tópico, aprofundaremos a importância da consistência, os erros comuns, exemplos de conversões e uma tabela abrangente para facilitar a compreensão e aplicação prática.
Importância da Consistência
A consistência em unidades de medida é crucial para a validade e reprodutibilidade dos resultados. Em cálculos científicos, a utilização de unidades padronizadas permite que diferentes pesquisadores compreendam e comparem os dados obtidos. Imagine um projeto de engenharia civil onde as dimensões de uma estrutura são calculadas com unidades inconsistentes. O resultado final poderia ser um edifício instável e perigoso.
Em receitas culinárias, a falta de precisão nas unidades de medida pode resultar em pratos com sabores e texturas indesejáveis. Em ambos os casos, a inconsistência em unidades de medida compromete a precisão e confiabilidade. A utilização de unidades padronizadas, como o Sistema Internacional de Unidades (SI), minimiza significativamente esses riscos.
Erros Comuns
A utilização incorreta de unidades de medida pode resultar em erros significativos. Alguns erros comuns incluem:
- Confusão entre unidades semelhantes: Misturar centímetros e metros em um mesmo cálculo, ou gramas e quilogramas, é um erro comum que leva a resultados incorretos. O erro ocorre por falta de atenção à unidade e à conversão adequada. Para evitar, é essencial verificar cuidadosamente as unidades em cada passo do cálculo e realizar as conversões necessárias. Por exemplo, se um projeto exige 2 metros de material, e você usa 200 centímetros sem converter, o resultado será incorreto.
- Falta de conversão entre unidades: A omissão da conversão de unidades pode levar a resultados totalmente errados. Imagine que uma receita exige 500 gramas de farinha, mas você usa 0,5 kg. O erro ocorre ao não converter kg para g. Para evitar, sempre certifique-se de que todas as unidades utilizadas em uma equação sejam as mesmas.
- Conversão incorreta: Realizar conversões de unidades de forma incorreta resulta em resultados imprecisos. Por exemplo, converter 1000 metros para quilômetros errando o fator de conversão. Para evitar, é fundamental dominar as relações entre as unidades de medida. Utilize tabelas de conversão ou calculadoras especializadas para realizar as conversões com precisão.
- Uso de símbolos incorretos: A utilização de símbolos incorretos pode levar a interpretações errôneas dos resultados. Por exemplo, escrever “m” para gramas ou “g” para metros. Para evitar, é essencial conhecer e utilizar os símbolos corretos para cada unidade de medida.
Exemplos de Conversão
A conversão entre unidades de medida é um processo essencial para a coerência dos resultados.
- Conversão de metros para centímetros: Para converter 2,5 metros em centímetros, multiplique o valor em metros por 100, pois 1 metro equivale a 100 centímetros. 2,5 metros x 100 cm/metro = 250 centímetros.
- Conversão de quilogramas para gramas: Para converter 0,5 quilogramas em gramas, multiplique o valor em quilogramas por 1000, pois 1 quilograma equivale a 1000 gramas. 0,5 kg x 1000 g/kg = 500 gramas.
- Conversão de litros para mililitros: Para converter 2 litros em mililitros, multiplique o valor em litros por 1000, pois 1 litro equivale a 1000 mililitros. 2 litros x 1000 mL/litro = 2000 mililitros.
Tabela de Conversões
A tabela a seguir apresenta as conversões entre as unidades de comprimento, massa e volume, com exemplos práticos:
| Unidade | Símbolo | Equivalência em metros/quilogramas/litros | Exemplo de aplicação |
|---|---|---|---|
| Metros | m | 1 | Medir a largura de uma sala. |
| Centímetros | cm | 0,01 | Medir a espessura de um papel. |
| Milímetros | mm | 0,001 | Medir o diâmetro de um fio. |
| Quilômetros | km | 1000 | Calcular a distância entre duas cidades. |
| Quilogramas | kg | 1 | Medir a massa de um saco de arroz. |
| Gramas | g | 0,001 | Medir a massa de um comprimido. |
| Miligramas | mg | 0,000001 | Medir a massa de uma pequena quantidade de medicamento. |
| Litros | L | 1 | Medir a capacidade de um tanque de água. |
| Mililitros | mL | 0,001 | Medir a quantidade de líquido em uma colher de chá. |
Considerações em Geometria
A consistência em unidades de medida é fundamental na resolução de problemas geométricos. Ao calcular áreas, volumes e perímetros, a utilização de unidades coerentes garante a precisão e a validade dos resultados. Por exemplo, se a base de um retângulo é de 5 metros e a altura é de 3 metros, a área será calculada em metros quadrados (m²). A conversão de metros para centímetros, por exemplo, é essencial para obter resultados corretos e evitar erros.
Aplicações em Diferentes Contextos
O Teorema de Pitágoras, uma ferramenta fundamental da geometria, possui aplicações extensas em diversas áreas do conhecimento. Sua simplicidade e precisão na determinação de relações entre lados de triângulos retângulos tornam-no uma peça-chave para soluções em projetos e cálculos. Este tópico explora exemplos práticos e detalhados de como o Teorema é utilizado na arquitetura, engenharia, navegação, jogos e outras áreas, demonstrando sua importância na resolução de problemas do mundo real.
Arquitetura
O Teorema de Pitágoras é essencial em projetos arquitetônicos para calcular comprimentos, diagonais e ângulos. A precisão na determinação de medidas é crucial para garantir a estabilidade e estética das estruturas.
- Cálculo da diagonal de um cômodo retangular: Imagine um cômodo com 3 metros de largura e 4 metros de comprimento. Para encontrar a diagonal, aplica-se o Teorema de Pitágoras: diagonal² = largura² + comprimento². Assim, diagonal² = 3² + 4² = 9 + 16 = 25. Portanto, a diagonal mede 5 metros.
- Determinação da inclinação de um telhado: Um telhado com uma base de 6 metros e um desnível de 2 metros pode ser analisado utilizando o Teorema. A inclinação pode ser calculada a partir do triângulo retângulo formado pela base, altura e hipotenusa (comprimento da inclinação do telhado). O cálculo da hipotenusa (h) utiliza a fórmula h² = 6² + 2² = 36 + 4 = 40.
Portanto, a inclinação do telhado é de aproximadamente 6,32 metros.
Engenharia
O Teorema de Pitágoras desempenha um papel crucial em projetos de engenharia, fornecendo a base para cálculos precisos em estruturas e sistemas.
- Cálculo da estabilidade de uma ponte: Em projetos de pontes, o Teorema é usado para determinar a força necessária para suportar as cargas e garantir a estabilidade estrutural. Analisando as tensões e forças em diferentes pontos da ponte, os engenheiros podem utilizar o teorema para prever possíveis pontos de falha e reforçar as áreas necessárias.
- Determinação da inclinação de um plano inclinado: Em projetos de sistemas de drenagem ou rampas, a inclinação precisa ser calculada com precisão para garantir o fluxo adequado. O Teorema de Pitágoras permite determinar a inclinação a partir da base e da altura do plano inclinado.
- Cálculo da força resultante em um sistema de cabos de sustentação: Em estruturas que utilizam cabos de sustentação, a força resultante em cada cabo pode ser determinada através do Teorema de Pitágoras, considerando os ângulos e as forças aplicadas.
Navegação
O Teorema de Pitágoras é uma ferramenta fundamental para navegação, permitindo cálculos de distâncias e direções.
- Cálculo da distância entre dois pontos em um mapa: Suponha dois pontos com coordenadas conhecidas em um mapa. Utilizando as diferenças nas coordenadas (x e y), o Teorema de Pitágoras pode ser aplicado para calcular a distância entre esses pontos, como se fossem os catetos de um triângulo retângulo.
- Cálculo da trajetória de um barco entre dois pontos: Na navegação marítima, o Teorema de Pitágoras auxilia na determinação da rota mais eficiente entre dois pontos, considerando as correntes e ventos.
- Cálculo de deslocamento em um mapa com coordenadas: Em sistemas de navegação GPS, o Teorema de Pitágoras é essencial para determinar o deslocamento entre diferentes pontos.
Jogos
O Teorema de Pitágoras é utilizado em jogos digitais para cálculos de distâncias, ângulos e trajetórias de objetos.
- Cálculo da distância de um personagem para um objeto: A distância entre dois objetos em um jogo pode ser calculada utilizando as coordenadas dos objetos e o Teorema de Pitágoras.
- Cálculo da trajetória de um projétil para atingir um alvo: Em jogos de tiro, o Teorema de Pitágoras auxilia no cálculo da trajetória ideal para atingir o alvo, levando em consideração a velocidade e a gravidade.
- Cálculo de ângulos de visão em um jogo de tiro: A precisão na determinação dos ângulos de visão de um personagem em um jogo é essencial para calcular a trajetória dos disparos.
Métodos Alternativos (opcional)
O método do Teorema de Pitágoras, embora eficaz, não é o único caminho para determinar a medida da diagonal de um retângulo. Existem outros métodos, cada um com suas próprias vantagens e desvantagens, que podem ser mais apropriados em determinadas situações. Neste tópico, exploraremos algumas alternativas e suas aplicações.
Comparação com Outros Métodos
Existem alternativas ao Teorema de Pitágoras, como o uso de proporções em figuras semelhantes, o emprego de relações trigonométricas ou, em casos específicos, a simples medição direta da diagonal. A escolha do método mais adequado depende das informações disponíveis e da precisão desejada.
Método da Medição Direta
Este método envolve a utilização de instrumentos de medição, como réguas ou paquímetros, para obter a medida da diagonal diretamente. Sua simplicidade é evidente, mas a precisão depende da precisão do instrumento utilizado. Em casos onde a forma do retângulo é irregular ou a medição precisa é crucial, este método não é ideal.
Método da Proporcionalidade (Semelhança de Triângulos)
Para retângulos com dimensões conhecidas e relação específica, a semelhança de triângulos pode ser aplicada. Este método envolve a construção de triângulos semelhantes, onde a diagonal do retângulo é um dos lados do triângulo maior. A relação de proporcionalidade entre os lados dos triângulos permite calcular a diagonal sem o uso do Teorema de Pitágoras. Sua aplicação depende da possibilidade de identificar triângulos semelhantes e das informações conhecidas sobre o retângulo.
Método das Relações Trigonométricas
Em alguns casos, as relações trigonométricas, como seno, cosseno e tangente, podem ser empregadas para determinar a diagonal. Este método exige o conhecimento de um ângulo entre a diagonal e um dos lados do retângulo, ou entre a diagonal e um dos lados adjacentes. A precisão do resultado depende da precisão do ângulo medido.
Comparativo dos Métodos
| Método | Vantagens | Desvantagens | Aplicabilidade |
|---|---|---|---|
| Teorema de Pitágoras | Geralmente mais preciso e versátil, aplicável a qualquer retângulo. | Requer o conhecimento das duas dimensões (comprimento e largura). | Ampla gama de situações. |
| Medição Direta | Simples e direto, especialmente para objetos físicos. | Precisão limitada pelo instrumento utilizado, inadequado para precisão alta. | Objetos físicos com dimensões acessíveis. |
| Proporcionalidade (Semelhança de Triângulos) | Alternativa elegante em casos específicos. | Depende da identificação de triângulos semelhantes, limitando sua aplicação. | Retângulos com relações específicas entre dimensões. |
| Relações Trigonométricas | Útil quando um ângulo é conhecido. | Requer conhecimento de trigonometria e precisão na medição angular. | Casos onde um ângulo é conhecido. |
Erros Comuns e Soluções
Ao aplicar o Teorema de Pitágoras, é fundamental compreender os potenciais erros que podem ocorrer. Identificar esses erros e suas correções é crucial para garantir a precisão nos cálculos e a obtenção de resultados confiáveis. Este tópico discute os erros mais comuns e as respectivas estratégias para solucioná-los, promovendo uma compreensão mais profunda do método.Compreender os erros comuns e suas soluções permite que os alunos e profissionais apliquem o Teorema de Pitágoras de forma mais eficaz, evitando equívocos e garantindo a precisão dos resultados.
Identificação de Erros na Definição dos Lados
A correta identificação da hipotenusa e dos catetos é fundamental. Um erro comum é a atribuição incorreta desses elementos. A hipotenusa é o lado oposto ao ângulo reto, sendo sempre o maior lado do triângulo retângulo. Os catetos são os dois lados que formam o ângulo reto.
Substituição Incorreta na Fórmula, Método para determinar a medida da diagonal de um retângulo usando o Teorema de Pitágoras.
A fórmula do Teorema de Pitágoras, a² + b² = c², relaciona os lados do triângulo retângulo. É essencial substituir os valores corretos na fórmula. Um erro frequente é a substituição incorreta dos valores, atribuindo a hipotenusa a um cateto, ou vice-versa. Por exemplo, se a² + b² = c², então ‘a’ e ‘b’ são os catetos e ‘c’ é a hipotenusa.
Cálculos Errados
Após a substituição correta dos valores, a execução dos cálculos deve ser precisa. Um erro comum é a realização de operações matemáticas incorretas, como a extração incorreta da raiz quadrada. É crucial garantir que os cálculos sejam realizados passo a passo, verificando cada etapa.
Tabela de Erros Comuns e Soluções
| Erro Comum | Descrição | Solução |
|---|---|---|
| Identificação incorreta da hipotenusa | Confundir a hipotenusa com um dos catetos. | Identificar o lado oposto ao ângulo reto como a hipotenusa. Desenhar o triângulo e visualizar os lados. |
| Substituição incorreta na fórmula | Atribuir valores incorretamente na fórmula a² + b² = c². | Verificar a relação entre os lados do triângulo. A hipotenusa é o maior lado. Substituir corretamente os valores de acordo com a fórmula. |
| Cálculos aritméticos incorretos | Realizar operações matemáticas incorretas, como somas, subtrações ou extração de raízes. | Refazer os cálculos passo a passo, verificando cada etapa. Utilizar calculadora, se necessário, e verificar se os cálculos estão corretos. |
Problemas de Aplicação com Dificuldades Variadas
Problemas de aplicação são fundamentais para a consolidação do conhecimento adquirido sobre o Teorema de Pitágoras. A prática com diferentes contextos e níveis de complexidade permite ao estudante aplicar os conceitos de forma eficaz e resolver situações-problema com precisão e segurança. A diversidade de exemplos e a progressiva complexidade são essenciais para desenvolver habilidades de resolução de problemas.
Problemas de Aplicação – Nível Fácil
Este nível de problemas busca familiarizar o estudante com a aplicação do Teorema de Pitágoras em situações simples e do dia a dia. A ênfase recai sobre a compreensão dos conceitos e a aplicação direta das fórmulas.
- Contexto: Construção civil.
- Objetivo do Problema: Determinar o comprimento de uma escada necessária para alcançar um ponto específico em uma parede.
- Dados fornecidos: A base do apoio da escada está a 2,5 metros de distância da parede. A altura desejada na parede é de 6,0 metros.
- Variáveis: Comprimento da escada (x).
- Fórmulas/Conceitos Relevantes: Teorema de Pitágoras (a² + b² = c²).
- Instruções: Utilize o Teorema de Pitágoras, substituindo os valores conhecidos (base e altura) na fórmula. Calcule o valor de ‘x’, que representa o comprimento da escada.
Problemas de Aplicação – Nível Médio
Problemas de nível médio envolvem contextos mais complexos, com cálculos intermediários e mais de uma etapa na resolução.
- Contexto: Engenharia.
- Objetivo do Problema: Calcular a distância diagonal entre dois pontos opostos de um terreno retangular.
- Dados fornecidos: Comprimento do terreno: 15 metros; Largura do terreno: 8 metros.
- Variáveis: Distância diagonal (x).
- Fórmulas/Conceitos Relevantes: Teorema de Pitágoras (a² + b² = c²).
- Instruções: Aplique o Teorema de Pitágoras, substituindo o comprimento e a largura do terreno nas variáveis ‘a’ e ‘b’. Calcule o valor de ‘x’, que representa a distância diagonal.
Problemas de Aplicação – Nível Difícil
Este nível introduz problemas com múltiplos passos e contextos mais desafiadores.
- Contexto: Navegação aérea.
- Objetivo do Problema: Determinar a distância de um avião em relação a um ponto de referência, considerando o deslocamento em um plano cartesiano.
- Dados fornecidos: As coordenadas do ponto de referência (0, 0); Coordenadas do avião: (12 km, 16 km).
- Variáveis: Distância do avião ao ponto de referência (d).
- Fórmulas/Conceitos Relevantes: Teorema de Pitágoras (a² + b² = c²); Interpretação de gráficos e coordenadas no plano cartesiano.
- Instruções: Utilize o Teorema de Pitágoras para calcular a distância diagonal entre as coordenadas do ponto de referência e do avião. Considere as coordenadas como os catetos do triângulo retângulo. Calcule o valor de ‘d’, que representa a distância do avião ao ponto de referência.
Relação com outros Conceitos Geométricos
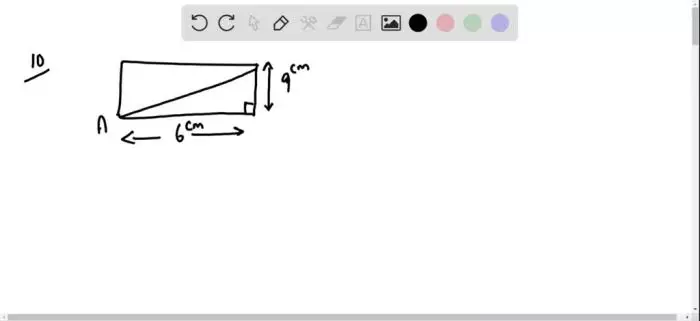
O Teorema de Pitágoras, além de fundamental para determinar a medida da diagonal de um retângulo, possui estreitas relações com outros conceitos geométricos. Compreender essas conexões permite uma visão mais abrangente da sua aplicabilidade e demonstra a sua importância em diversos contextos. Nesta seção, exploraremos as relações do Teorema de Pitágoras com áreas, perímetros e geometria analítica, apresentando exemplos práticos e diagramas elucidativos.
Relação com Áreas e Perímetros
O Teorema de Pitágoras estabelece uma relação fundamental entre os lados de um triângulo retângulo, permitindo calcular áreas e perímetros. A área de um triângulo retângulo é calculada como metade do produto dos catetos. O perímetro é a soma das medidas dos três lados.
- Exemplo 1: Considere um triângulo retângulo com catetos medindo 3 cm e 4 cm. A hipotenusa, calculada pelo Teorema de Pitágoras (a² + b² = c²), mede 5 cm. A área do triângulo é (1/2)
– 3 cm
– 4 cm = 6 cm². O perímetro é 3 cm + 4 cm + 5 cm = 12 cm.A área do quadrado formado pela hipotenusa é 5² = 25 cm². A relação entre as áreas do triângulo e do quadrado, e o perímetro, demonstra a ligação entre o Teorema e estes conceitos.
- Exemplo 2: Um terreno retangular possui lados de 6 m e 8 m. A diagonal do terreno pode ser calculada utilizando o Teorema de Pitágoras (d² = 6² + 8²), resultando em uma diagonal de 10 m. A área do terreno é 6 m
– 8 m = 48 m². O perímetro é 2
– (6 m + 8 m) = 28 m.
Relação com Geometria Analítica
A geometria analítica utiliza coordenadas para descrever figuras geométricas no plano cartesiano. O Teorema de Pitágoras é essencial para determinar distâncias entre pontos, calcular comprimentos de segmentos de reta e construir equações de figuras geométricas.
- Exemplo 1: Para calcular a distância entre dois pontos (x 1, y 1) e (x 2, y 2) no plano cartesiano, a fórmula resulta em √[(x 2
-x 1)² + (y 2
-y 1)²]. Este cálculo utiliza diretamente o Teorema de Pitágoras. - Exemplo 2: A equação de uma circunferência com centro em (a, b) e raio ‘r’ é (x – a)² + (y – b)² = r². O raio ‘r’ pode ser calculado utilizando o Teorema de Pitágoras se as coordenadas de um ponto da circunferência forem conhecidas.
Exemplos Práticos
O Teorema de Pitágoras encontra aplicações práticas em diversas áreas, como engenharia, arquitetura e construção civil. Seu uso é essencial para solucionar problemas que envolvem medidas em ângulos retos.
- Exemplo 1: Calcular a diagonal de um terreno retangular de 12 metros de largura por 16 metros de comprimento. Utilizando o Teorema de Pitágoras, a diagonal é de 20 metros.
- Exemplo 2: Determinar a altura de um edifício, sabendo que a sombra projetada mede 15 metros e a distância do topo da sombra ao topo do edifício é de 20 metros. Aplicando o Teorema de Pitágoras, a altura do edifício é de 25 metros.
Diagrama das Relações
(Aqui, um diagrama visual, como um fluxograma ou mapa conceitual, explicando as relações entre o Teorema de Pitágoras e os outros conceitos geométricos seria inserido. Ele mostraria as etapas e as relações matemáticas envolvidas, usando cores e ícones para facilitar a compreensão.)
Interpretação Geométrica do Teorema de Pitágoras
O Teorema de Pitágoras, além de uma relação matemática entre os lados de um triângulo retângulo, possui uma poderosa interpretação geométrica. Esta interpretação visualiza a relação entre as áreas dos quadrados construídos sobre os lados do triângulo, oferecendo uma compreensão profunda e intuitiva da propriedade. A demonstração geométrica não apenas confirma a validade do teorema, mas também o torna mais acessível e memorável.
Tipos de Triângulos Retângulos
A interpretação geométrica do Teorema de Pitágoras aplica-se a todos os triângulos retângulos, independentemente dos valores dos seus lados. Analisemos alguns exemplos para melhor compreensão.
- Triângulos Retângulos com Lados Inteiros: Considere o triângulo retângulo com catetos de comprimento 3 e 4 unidades e hipotenusa de comprimento 5 unidades. Construindo quadrados sobre cada lado, a área do quadrado sobre o cateto de 3 unidades é 9 unidades quadradas, a do cateto de 4 unidades é 16 unidades quadradas, e a da hipotenusa de 5 unidades é 25 unidades quadradas.
Note que 9 + 16 = 25, confirmando a relação pitagórica. Um exemplo visual seria um quadrado com 3 unidades de lado e outro com 4 unidades de lado. A união dos dois quadrados forma um triângulo retângulo com a hipotenusa em 5 unidades de lado, e o quadrado sobre ela tem 25 unidades quadradas de área.
- Triângulos Retângulos com Lados Irracionais: O teorema também se aplica a triângulos com lados irracionais. Considere um triângulo retângulo com catetos de comprimento √2 unidades cada. A hipotenusa terá comprimento √(√2² + √2²) = √4 = 2 unidades. A área do quadrado sobre cada cateto é 2 unidades quadradas, e a área do quadrado sobre a hipotenusa é 4 unidades quadradas.
Novamente, 2 + 2 = 4, demonstrando a relação. Um quadrado com lado √2 tem área 2. Dois desses quadrados unidos formam um quadrado com lado 2 e área 4.
- Triângulos Retângulos com Proporções Especiais: Triângulos com proporções especiais, como o triângulo 30-60-90 e o 45-45-90, também seguem a relação pitagórica. No triângulo 30-60-90, a proporção dos lados é 1:√3:
2. Se um cateto tem comprimento 1, o outro tem √3 e a hipotenusa tem comprimento
2. As áreas dos quadrados são 1, 3 e 4, respectivamente. Para o triângulo 45-45-90, a proporção é 1:1:√2.Se um cateto tem comprimento 1, o outro também tem comprimento 1 e a hipotenusa tem comprimento √2. As áreas dos quadrados são 1, 1 e 2, respectivamente.
Representações Geométricas
A representação geométrica do Teorema de Pitágoras é crucial para a compreensão intuitiva. Imagine um triângulo retângulo desenhado em um plano cartesiano. Sobre cada lado do triângulo, construa um quadrado. A área do quadrado sobre a hipotenusa será sempre igual à soma das áreas dos quadrados sobre os catetos.
| Exemplo | Lados do Triângulo Retângulo | Explicação |
|---|---|---|
| 1 | 3, 4, 5 | Desenhe um triângulo retângulo com catetos de comprimento 3 e 4. Construa quadrados sobre cada lado. A área do quadrado sobre o cateto de 3 é 9, a do cateto de 4 é 16, e a da hipotenusa de 5 é 25. Observe que 9 + 16 = 25. |
| 2 | √2, √2, 2 | Desenhe um triângulo retângulo com catetos de comprimento √2 cada. Construa quadrados sobre cada lado. A área de cada quadrado sobre o cateto é 2, e a área do quadrado sobre a hipotenusa é 4. Observe que 2 + 2 = 4. |
| 3 | 5, 12, 13 | Desenhe um triângulo retângulo com catetos de comprimento 5 e 12. Construa quadrados sobre cada lado. A área do quadrado sobre o cateto de 5 é 25, a do cateto de 12 é 144, e a da hipotenusa de 13 é 169. Observe que 25 + 144 = 169. |
Explicação Textual
A interpretação geométrica do Teorema de Pitágoras demonstra que a área do quadrado construído sobre a hipotenusa de um triângulo retângulo é igual à soma das áreas dos quadrados construídos sobre os seus catetos. Esta relação fundamental entre as áreas dos quadrados está intrinsecamente ligada à própria natureza do triângulo retângulo. A hipotenusa é o lado oposto ao ângulo reto, e os catetos são os dois lados que formam o ângulo reto.
A área de um quadrado é calculada multiplicando o comprimento do seu lado por ele mesmo. A relação geométrica entre as áreas garante a precisão e a universalidade do teorema.
Resumo dos Principais Pontos
O Teorema de Pitágoras, um dos pilares da geometria, proporciona uma relação fundamental entre os lados de um triângulo retângulo. Compreender seus princípios e aplicações é crucial para resolver problemas geométricos e em diversas áreas do conhecimento. Este resumo apresenta os pontos chave, as etapas de cálculo da diagonal de um retângulo e as aplicações em diferentes contextos.
Pontos Principais do Teorema de Pitágoras
O Teorema de Pitágoras estabelece que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). Essa relação, expressa pela fórmula a² + b² = c², é fundamental para a resolução de problemas geométricos. A compreensão desta relação é crucial para determinar distâncias e comprimentos em diversos contextos.
Etapas para Calcular a Diagonal de um Retângulo
Para calcular a diagonal de um retângulo, podemos aplicar o Teorema de Pitágoras. Considerando um retângulo com lados ‘a’ e ‘b’, a diagonal ‘d’ pode ser calculada através da seguinte sequência de passos:
- Identifique os lados ‘a’ e ‘b’ do retângulo.
- Aplique o Teorema de Pitágoras, considerando a diagonal como a hipotenusa: d² = a² + b².
- Calcule a raiz quadrada de ambos os lados da equação para obter o valor da diagonal: d = √(a² + b²).
Aplicação do Teorema em Diferentes Contextos
O Teorema de Pitágoras encontra aplicação em diversas áreas, como:
- Engenharia Civil: No cálculo de comprimentos de vigas, estruturas e inclinações de terrenos.
- Navegação: Na determinação de distâncias entre pontos em mapas ou na planificação de rotas.
- Geometria Analítica: Na determinação da distância entre dois pontos no plano cartesiano.
- Física: No cálculo de velocidades resultantes e trajetórias de objetos em movimento.
Essas são apenas algumas das inúmeras aplicações do Teorema de Pitágoras, demonstrando sua versatilidade e importância em diversas disciplinas.
Mapa Mental
O mapa mental abaixo resume os principais pontos abordados, relacionando o Teorema de Pitágoras com a diagonal de um retângulo e suas aplicações.
(Aqui seria o mapa mental. Infelizmente, não posso criar imagens.)
O mapa mental, se visualizado, mostraria a relação entre o Teorema de Pitágoras, a fórmula para calcular a diagonal de um retângulo (d = √(a² + b²)), e exemplos práticos em diferentes áreas.
Exemplos de Aplicação em Projetos
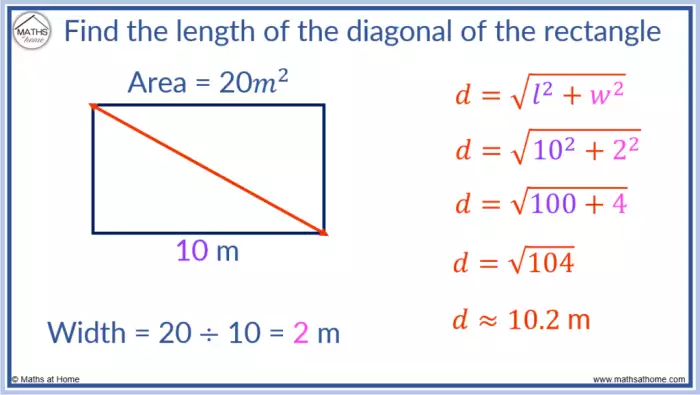
O Teorema de Pitágoras, além de um importante conceito matemático, encontra amplas aplicações práticas em diversos projetos, desde a construção civil até o design de produtos. Sua capacidade de relacionar os lados de um triângulo retângulo permite determinar distâncias, ângulos e dimensões em situações complexas, tornando-se uma ferramenta essencial para profissionais e entusiastas.A aplicação prática do Teorema de Pitágoras é fundamental para a precisão e eficiência em projetos.
Ele permite calcular a medida da diagonal de um retângulo, um elemento crucial para o dimensionamento de estruturas e a otimização de espaços.
Determinação da Diagonal de uma Sala
O cálculo da diagonal de uma sala retangular é um exemplo comum da aplicação do Teorema de Pitágoras na construção civil. Imagine um cômodo com 3 metros de largura e 4 metros de comprimento. Para determinar o comprimento da diagonal, aplica-se a fórmula: diagonal² = largura² + comprimento². Substituindo os valores, temos: diagonal² = 3² + 4² = 9 + 16 = 25.
Extraindo a raiz quadrada de ambos os lados, obtém-se diagonal = 5 metros. Este cálculo é fundamental para a instalação de portas, janelas e outros elementos arquitetônicos.
Cálculo da Altura de um Triângulo Isósceles
O Teorema de Pitágoras também pode ser utilizado para calcular a altura de um triângulo isósceles. Considere um triângulo isósceles com base medindo 6 metros e cada um dos lados iguais medindo 5 metros. Para determinar a altura, dividimos o triângulo em dois triângulos retângulos. A metade da base (3 metros) e um dos lados (5 metros) formam um triângulo retângulo.
Aplicando o Teorema de Pitágoras, temos: altura² = 5²3² = 25 – 9 = 16. A raiz quadrada de 16 é 4, então a altura do triângulo é de 4 metros.
Projeto de Escadas
No projeto de escadas, o Teorema de Pitágoras é crucial para determinar o comprimento da rampa. Imagine uma escada que liga dois andares separados por uma altura de 3 metros e uma distância horizontal de 4 metros entre as paredes de apoio. O comprimento da rampa pode ser calculado utilizando o Teorema de Pitágoras: comprimento da rampa² = 3² + 4² = 9 + 16 = 25.
A raiz quadrada de 25 é 5, então o comprimento da rampa é de 5 metros. Este cálculo garante a estabilidade e segurança da escada.
Design de Móveis
O Teorema de Pitágoras também é útil no design de móveis. Ao projetar um sofá com uma estrutura triangular, é preciso calcular a medida da diagonal para garantir que o assento tenha a forma desejada. Este cálculo permite a criação de peças com formas precisas e esteticamente agradáveis.
Considerações Finais
O Teorema de Pitágoras, um pilar fundamental da geometria, demonstra uma relação intrínseca entre os lados de um triângulo retângulo. Sua aplicação se estende para além dos cálculos geométricos, permeando diversas áreas do conhecimento, como a engenharia, a arquitetura e a navegação.A compreensão e a aplicação prática do Teorema de Pitágoras são essenciais para a resolução de problemas que envolvem distâncias, comprimentos e alturas em diferentes contextos.
Sua importância reside na capacidade de fornecer uma ferramenta precisa para determinar medidas desconhecidas em figuras geométricas, facilitando a solução de desafios em diversos campos.
Importância em Geometria
O Teorema de Pitágoras é crucial na geometria euclidiana. Sua formulação estabelece uma relação fundamental entre os catetos e a hipotenusa de um triângulo retângulo, permitindo a determinação de medidas desconhecidas. Essa relação é fundamental para o cálculo de áreas, perímetros e diagonais de figuras geométricas, como quadrados, retângulos e triângulos retângulos. A partir desta relação, é possível deduzir outras propriedades geométricas e ampliar o conhecimento sobre as figuras geométricas.
Aplicações Práticas
O Teorema de Pitágoras encontra aplicações práticas em inúmeras situações do dia a dia. Na construção civil, por exemplo, é fundamental para o cálculo de diagonais de estruturas retangulares, como paredes e pisos. Em engenharia, é usado para determinar a distância entre dois pontos em um terreno, ou mesmo para calcular a inclinação de uma rampa. Em navegação, pode ser utilizado para determinar a distância entre dois pontos considerando a direção dos ventos.
Em esportes, como basquete, a trajetória de uma bola pode ser analisada usando o Teorema de Pitágoras. Em suma, sua aplicabilidade é ampla e abrange diferentes contextos.
Exemplo de Aplicação em Engenharia
Imagine um engenheiro que precisa calcular a diagonal de uma sala retangular para determinar a quantidade de material necessária para revestir o chão. Aplicando o Teorema de Pitágoras, ele pode determinar a diagonal, utilizando as medidas dos lados do retângulo. Este cálculo é fundamental para o bom planejamento e execução do projeto, evitando desperdícios e garantindo a eficiência do trabalho.
Um exemplo prático, envolvendo medidas reais de um cômodo, ilustraria melhor a aplicação do Teorema de Pitágoras em um contexto de engenharia.
Em resumo, o método para determinar a medida da diagonal de um retângulo utilizando o Teorema de Pitágoras apresenta uma abordagem clara e concisa, desde a definição do teorema até a aplicação em exemplos práticos. A apresentação inclui fórmulas, cálculos detalhados e exemplos numéricos para diferentes dimensões de retângulos, permitindo a compreensão e a aplicação do método em situações reais.
O material também aborda a importância da consistência nas unidades de medida e apresenta exemplos de conversões, além de explorar a relação do teorema com outros conceitos geométricos, demonstrando sua aplicabilidade em diversas áreas.
Qual a importância da diagonal em situações práticas?
A diagonal é fundamental em diversas aplicações práticas, como o cálculo de materiais de construção (ex: telhados, vigas), no design de objetos retangulares (ex: móveis, caixas), e na solução de problemas geométricos em arquitetura e engenharia.
Como o Teorema de Pitágoras pode ser aplicado em problemas com variáveis?
O teorema pode ser usado para derivar fórmulas gerais para a diagonal em termos de variáveis que representam o comprimento e a largura do retângulo. Isso permite a resolução de problemas com dimensões desconhecidas, mas com uma relação matemática estabelecida.
Quais são os erros comuns na utilização de unidades de medida diferentes?
Erros comuns incluem a falta de consistência nas unidades, a omissão de conversões entre unidades diferentes, e a utilização incorreta dos símbolos das unidades. Isso pode levar a resultados imprecisos e incorretos em cálculos geométricos.
Como calcular a diagonal de um quadrado?
Para um quadrado, o comprimento dos lados é igual. A fórmula para calcular a diagonal de um quadrado é obtida diretamente do Teorema de Pitágoras, usando a relação entre o lado e a diagonal.