Com o desafio “Assinale A Alternativa Que Representa Corretamente O Valor Da Seguinte Expressão”, embarque em uma aventura matemática! Preparamos um mergulho profundo nos mistérios das expressões matemáticas, explorando desde operações aritméticas simples até funções complexas. Prepare-se para desvendar os segredos por trás dos cálculos, aprendendo a identificar a alternativa correta entre um mar de possibilidades. Acompanhe cada passo, da introdução às expressões com variáveis, funções e até mesmo problemas desafiadores.
Será uma jornada fascinante!
Vamos desvendar os enigmas matemáticos, descobrindo as etapas cruciais para encontrar a resposta correta. Exploraremos diferentes tipos de expressões, desde as mais básicas até as mais complexas, e aprenderemos a resolver cada uma com clareza e precisão.
Introdução à Expressão Matemática

Source: z-dn.net
Olá, exploradores da matemática! Preparamos uma jornada divertida para desvendar os mistérios das expressões matemáticas. A frase “Assinale a alternativa que representa corretamente o valor da seguinte expressão” é uma porta de entrada para um mundo de cálculos, operações e descobertas. Vamos mergulhar nesse universo!As expressões matemáticas, representadas por símbolos e números, podem ser muito mais abrangentes do que você imagina.
Elas não se limitam apenas a operações aritméticas básicas, mas também abarcam conceitos de álgebra, geometria e cálculo.
Tipos de Expressões Matemáticas
As expressões matemáticas que a frase “Assinale a alternativa…” pode representar são vastas e diversificadas. Desde simples adições e subtrações até equações complexas envolvendo funções, variáveis e constantes, a matemática oferece um vasto leque de possibilidades.
- Expressões Aritméticas: Envolvem operações básicas como adição, subtração, multiplicação, divisão, potenciação e radiciação. Exemplos: 5 + 3, 12 / 4, 2 3, √9.
- Expressões Algébricas: Incluem variáveis, constantes e operadores, representando relações matemáticas. Exemplos: 2x + 5, x 2
-4, 3y/z. - Expressões com Funções: Utilizam funções matemáticas pré-definidas como seno, cosseno, logaritmo, exponencial, etc. Exemplos: sen(x), log(y), e x.
Componentes Essenciais de uma Expressão Matemática
Compreender os elementos que compõem uma expressão é crucial para sua avaliação.
- Operadores: Símbolos que indicam as operações a serem realizadas (por exemplo, +, -, ×, ÷, ^, √). São os comandos que guiam os cálculos.
- Variáveis: Letras ou símbolos que representam valores desconhecidos ou que podem variar (por exemplo, x, y, z). Pensando em variáveis como “espaços vazios” que podem receber valores diferentes.
- Constantes: Valores fixos e conhecidos (por exemplo, 2, 5, π). São os números com valores inalteráveis.
A Importância da Ordem das Operações
A ordem em que as operações são realizadas em uma expressão matemática é fundamental para obter o resultado correto. A regra PEMDAS (Parênteses, Expoentes, Multiplicação e Divisão, Adição e Subtração) ou BODMAS (Parênteses, Ordem, Divisão e Multiplicação, Adição e Subtração) define a prioridade das operações. Seguir essa ordem evita ambiguidades e garante precisão.
Exemplo: Em “2 + 3 × 4”, a multiplicação é realizada antes da adição, resultando em 14.
Quadro Comparativo de Expressões Matemáticas
| Tipo de Expressão | Características | Exemplos |
|---|---|---|
| Aritmética | Operações básicas com números. | 10 – 2, 5 × 3, 7 ÷ 1 |
| Algébrica | Envolvem variáveis e constantes. | 2x + 5, x2
|
| Função | Utilizam funções matemáticas. | sen(x), log(y), ex |
Expressões com Funções
As expressões matemáticas envolvendo funções são fundamentais para modelar e analisar diversos fenômenos. Compreender diferentes tipos de funções, suas propriedades e representações gráficas é crucial para a resolução de problemas em áreas como física, engenharia e ciências da computação. Este conteúdo explora as funções matemáticas mais comuns em expressões algébricas, permitindo identificar, aplicar suas propriedades e visualizar seus gráficos.
Funções Matemáticas
As funções matemáticas são relações que associam cada valor de entrada (argumento) a um único valor de saída (valor da função). Existem diversos tipos de funções, cada uma com suas características específicas. Algumas das funções mais frequentemente encontradas em expressões matemáticas são as funções trigonométricas, exponenciais, logarítmicas e polinomiais.
- Funções Trigonométricas: Estas funções relacionam ângulos a razões entre lados de triângulos retângulos. As mais comuns são seno (sen), cosseno (cos) e tangente (tan). Suas notações, como sen(x), cos(x) e tan(x), representam a aplicação da função a um valor x.
- Funções Exponenciais: Estas funções representam a variação exponencial de uma quantidade em relação a outra. A função exponencial mais fundamental é a função ex, onde e é a constante de Euler (aproximadamente 2.718). Outras funções exponenciais utilizam diferentes bases.
- Funções Logarítmicas: Essas funções são o inverso das funções exponenciais. A função logarítmica na base b, representada por log b(x), indica o expoente ao qual a base b deve ser elevada para obter o valor x.
- Funções Polinomiais: Funções definidas por polinômios. Exemplos incluem funções quadráticas (x 2), cúbicas (x 3) e assim por diante. A notação x n representa a potência n de x.
- Outras Funções Elementares: Funções como a raiz quadrada (√x) também são consideradas elementares e frequentemente aparecem em expressões.
Identificação em Alternativas
Para identificar as funções matemáticas em alternativas de um problema, é necessário reconhecer as notações matemáticas e os padrões das relações matemáticas. Por exemplo, a presença de símbolos como log, sen, cos, ou a representação de uma potência indica a presença de uma função específica.
Propriedades das Funções
As propriedades das funções, como paridade (par ou ímpar), domínio, imagem, intervalos de crescimento e decrescimento, fornecem insights sobre o comportamento da função. Reconhecer essas propriedades auxilia na análise e resolução de problemas.
Exemplos de Expressões
A seguir, exemplos de expressões matemáticas que utilizam funções trigonométricas, exponenciais e logarítmicas.
- Exemplo 1: sen(x) + 2e x. Esta expressão combina uma função trigonométrica (seno) com uma função exponencial.
- Exemplo 2: log 10(x 2 + 1). Esta expressão utiliza uma função logarítmica na base 10 aplicada a uma função polinomial.
- Exemplo 3: 3cos(πx)ln(x). Esta expressão envolve uma função trigonométrica (cosseno), uma função exponencial (ln) e um fator constante.
Representação Gráfica
A visualização gráfica de uma função fornece uma compreensão intuitiva de seu comportamento. Os gráficos a seguir ilustram os exemplos acima. Os gráficos demonstram os pontos importantes, como interseções com os eixos e assíntotas. Observe que os gráficos são simplificados para fins didáticos. A precisão dos gráficos pode ser melhorada usando ferramentas de plotagem.
Exemplo 1 (sen(x) + 2ex): O gráfico apresenta uma curva que oscila entre valores positivos e negativos, influenciada pela função seno e crescente exponencialmente pela função exponencial. Observe a oscilação periódica e o crescimento contínuo.
Exemplo 2 (log10(x 2 + 1)): O gráfico exibe uma curva crescente que se aproxima de um valor assintótico em valores positivos de x, exibindo o comportamento logarítmico e a adição de um polinômio.
Exemplo 3 (3cos(πx)
-ln(x)): O gráfico mostra uma curva oscilante que diminui conforme x aumenta. A curva é influenciada pelo cosseno, exibindo periodicidade, e pela função ln, que decresce monotonamente. Observe o comportamento assintótico próximo a x = 0.
Exercícios de Aplicação
Os exercícios a seguir envolvem a simplificação de expressões utilizando funções matemáticas, demonstrando a aplicação de propriedades e a resolução passo a passo.
- Simplifique a expressão: sen(x) 2 + cos(x) 2.
Solução: Utilizando a identidade trigonométrica fundamental sen 2(x) + cos 2(x) = 1, a expressão simplifica para 1.
Análise de Alternativas

Source: z-dn.net
Desvendando os segredos por trás das expressões matemáticas, vamos agora mergulhar na análise das alternativas. Imagine que você está em um labirinto, e cada alternativa é um corredor possível. Como saber qual caminho leva à solução correta? A chave está em entender os conceitos, as propriedades e, principalmente, os erros mais comuns.Para desvendar o caminho certo, precisamos de uma lupa para identificar os detalhes, um detector de mentiras para identificar erros e um mapa para comparar as diferentes alternativas.
Vamos embarcar nessa jornada de descobertas matemáticas!
Exemplos de Expressões com Múltiplas Alternativas
Para ilustrar, considere a expressão: Simplifique (3x² + 5x – 2)(2x²
3x + 1). As alternativas poderiam ser
- x² + 8x – 3
- x² + 2x – 1
- 5x² + 2x – 3
- x² + 8x + 1
Cada alternativa representa uma possível solução. A chave está em aplicar as regras matemáticas corretamente para encontrar a correta.
Métodos para Avaliar a Correção das Alternativas
A verificação da correção envolve uma série de etapas. Primeiramente, precisamos entender o problema, identificar as operações e suas prioridades. Depois, devemos aplicar a propriedade distributiva e simplificar os termos semelhantes. Por fim, comparamos o resultado com as alternativas propostas.Um método fundamental é a substituição de valores. Se você escolher um valor para x e obter um resultado diferente para cada alternativa, pode isolar a alternativa correta.
Essa estratégia permite identificar possíveis erros de cálculo.
Comparação e Contraste de Alternativas Incorretas com a Correta
Vamos analisar os erros comuns. Na alternativa incorreta “5x² + 2x – 3”, por exemplo, o erro pode estar na combinação incorreta dos termos semelhantes. O termo 3x² foi talvez incorretamente agrupado. Em “x² + 8x + 1”, talvez tenha ocorrido um erro na subtração dos termos constantes.
Quadro Comparativo de Alternativas
| Alternativa | Correta? | Pontos-Chave |
|---|---|---|
| x² + 8x – 3 | Sim | Combinação correta dos termos semelhantes, aplicação correta da propriedade distributiva. |
| x² + 2x – 1 | Não | Erro na simplificação dos termos semelhantes. |
| 5x² + 2x – 3 | Não | Erro na combinação dos termos semelhantes após a distribuição. |
| x² + 8x + 1 | Não | Erro no cálculo da subtração. |
Avaliação da Validade de Cada Alternativa
Para validar cada alternativa, precisamos seguir as regras matemáticas e verificar se a solução está de acordo com os princípios algébricos. É fundamental entender as etapas da solução para encontrar a alternativa correta. Em resumo, é preciso “decompor” cada alternativa para verificar se cada etapa está de acordo com as regras matemáticas. Substituir valores pode auxiliar a identificar erros e a confirmar se o resultado é consistente com o problema.
Problemas Complexos
Prepare-se para mergulhar em expressões matemáticas que desafiam até os matemáticos mais experientes! Nesta seção, exploraremos problemas complexos, desvendando os segredos para simplificá-los e resolvê-los. Aprenda técnicas essenciais para dominar essas equações e abrir portas para a compreensão de conceitos mais profundos.
Exemplos de Expressões Matemáticas Complexas
Diversas expressões podem ser consideradas complexas, dependendo do nível de conhecimento e habilidades matemáticas. Aqui estão alguns exemplos, envolvendo operações combinadas, frações, raízes e exponenciais:
- (3x 2 + 2x – 1) / (x – 2) + 5√(x+3)
- 2 3x
-7 2 + log 10(100)
-2√(49) - (x 2 + 4x + 4) / (x + 2)
– sin(π/4) - ∫ 0π sen(x) dx
Passos para Simplificar e Avaliar Expressões Complexas
Para simplificar e avaliar expressões matemáticas complexas, é fundamental seguir uma sequência lógica de passos. A chave está em desmembrar o problema em partes menores e mais gerenciáveis.
- Identificar as Operações: Determine os tipos de operações presentes na expressão (adição, subtração, multiplicação, divisão, potenciação, radiciação, logaritmos, funções trigonométricas etc.).
- Priorizar Operações: Siga a ordem das operações (PEMDAS/BODMAS – Parênteses/Colchetes, Expoentes/Raízes, Multiplicação/Divisão, Adição/Subtração) para garantir a precisão nos cálculos.
- Simplificar Termos Semelhantes: Se possível, combine termos semelhantes dentro dos parênteses ou em partes da expressão para facilitar a resolução.
- Resolver Funções: Avalie as funções trigonométricas, logarítmicas e outras funções presentes na expressão, substituindo os valores apropriados.
- Substituir Variáveis: Caso a expressão contenha variáveis, substitua-as pelos valores correspondentes.
- Calcular Valores: Execute as operações na ordem correta, lembrando-se da ordem das operações.
Métodos e Técnicas para Resolver Problemas com Várias Etapas
Resolver problemas matemáticos com múltiplas etapas requer organização e atenção aos detalhes. Aqui estão alguns métodos e técnicas:
- Decompor o Problema: Dividir o problema complexo em subproblemas mais simples, resolvendo-os sequencialmente.
- Desenvolver Estratégias: Utilizar técnicas específicas, como a fatoração, a complementação de quadrados ou a utilização de fórmulas para resolver partes específicas da expressão.
- Desenhar Diagramas ou Gráficos: Para problemas geométricos ou de aplicação, diagramas ou gráficos podem ajudar a visualizar a situação e identificar as relações entre as variáveis.
Quadro para Resolução de Expressões
Este quadro resume os passos para resolver expressões matemáticas complexas, facilitando a organização e o acompanhamento da resolução.
| Passo | Ação |
|---|---|
| 1 | Identificar as Operações |
| 2 | Priorizar Operações (PEMDAS/BODMAS) |
| 3 | Simplificar Termos Semelhantes |
| 4 | Resolver Funções |
| 5 | Substituir Variáveis |
| 6 | Calcular Valores |
Exemplos de Expressões Complexas e Resultados
Observe os exemplos a seguir com suas soluções:
- Expressão: (2x + 3) 2
-4x + 5, para x = 2
Resultado: 21 - Expressão: 2√(x 2 + 4) + log 10(1000), para x = 0
Resultado: 10
Erros Comuns e Interpretações Ambíguas
Olá, futuros mestres da matemática! Se você já se deparou com uma expressão matemática e sentiu que havia mais de uma forma de interpretá-la, saiba que não está sozinho. Interpretações ambíguas são comuns, e entender como evitá-las é fundamental para garantir resultados precisos. Vamos mergulhar nesse universo de potenciais equívocos e aprender a desvendá-los.
Erros Comuns na Avaliação de Expressões
A ordem das operações é crucial na matemática. Um erro comum é a falta de atenção à precedência de operações, como multiplicação e divisão antes de adição e subtração. Outro erro recorrente é o uso inadequado de parênteses, colchetes e chaves, que podem mudar completamente o resultado da expressão. Por exemplo, (2 + 3) × 4 é diferente de 2 + (3 × 4).
A imprecisão na notação pode levar a resultados incorretos.
Interpretações Ambíguas em Expressões Matemáticas
Expressões matemáticas podem ser ambíguas se não forem escritas de forma clara e precisa. Símbolos como o uso de barra (/) em expressões como 10/2+3 podem gerar dúvidas sobre se a divisão é prioritária ou não. A falta de clareza na utilização de expoentes e raízes quadradas pode levar a diferentes interpretações. Imagine a expressão 2x 2 + 3y – 5z.
Se não for claro qual variável está sendo elevada ao quadrado, a expressão torna-se ambígua.
Exemplos de Expressões com Múltiplas Interpretações
Vejamos alguns exemplos para ilustrar melhor esse ponto:
- A expressão “5 + 2 × 3” pode ser interpretada como (5 + 2) × 3 = 21 ou 5 + (2 × 3) = 11. A ordem das operações determina o resultado.
- A expressão “12 / 3 × 4” é ambígua. Ela pode ser interpretada como (12 / 3) × 4 = 16 ou 12 / (3 × 4) = 1. A ausência de parênteses torna a expressão confusa.
- A expressão “√4 + 9” pode ser interpretada como √(4 + 9) = √13 ou como √4 + 9 = 2 + 9 = 11. A correta interpretação depende de onde estão os parênteses imaginários.
Quadro Comparativo de Erros Comuns e suas Correções
| Erro Comum | Descrição | Correção |
|---|---|---|
| Ignorar a ordem das operações | Realizar operações fora da ordem estabelecida (ex: adição antes da multiplicação). | Utilizar a regra PEMDAS (Parênteses, Expoentes, Multiplicação e Divisão, Adição e Subtração) para garantir a ordem correta das operações. |
| Uso inadequado de parênteses | Ausência ou posicionamento incorreto de parênteses, colchetes e chaves. | Utilizar parênteses para especificar a ordem das operações e evitar ambiguidades. |
| Interpretação ambígua de símbolos | Símbolos como barra (/) podem ter diferentes interpretações. | Utilizar parênteses para definir a ordem das operações e evitar ambiguidades. |
Como Evitar Interpretações Ambíguas em Expressões Matemáticas
Para evitar erros e garantir que a expressão seja interpretada corretamente, é fundamental:
- Utilizar parênteses para indicar a ordem das operações.
- Escrever as expressões de forma clara e precisa, utilizando a notação matemática correta.
- Reescrever expressões com ambiguidade para remover qualquer dúvida.
- Verificar a ordem das operações com cuidado.
Métodos de Resolução de Expressões Matemáticas
Source: gauthmath.com
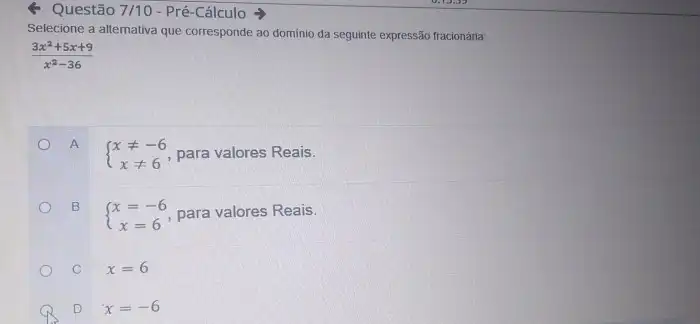
A matemática, como ferramenta universal, apresenta diversos métodos para resolver expressões. Compreender e aplicar esses métodos de forma adequada é crucial para obter resultados precisos e demonstrar um raciocínio lógico. Dominar esses métodos permite abordar problemas matemáticos com confiança e eficiência, desde operações aritméticas básicas até equações e inequações mais complexas.A escolha do método mais apropriado depende da estrutura da expressão matemática, permitindo resolver o problema com a menor quantidade de passos e maior precisão.
Analisar a expressão, identificar as operações e variáveis presentes é fundamental para selecionar o método mais eficaz.
Listagem de Métodos
Existem diversos métodos para resolver expressões matemáticas, cada um com suas características e aplicações específicas. A seguir, são apresentados alguns dos métodos mais comuns e relevantes para expressões matemáticas básicas.
- Método da Substituição: Utilizado para expressões com variáveis, onde valores específicos são atribuídos a essas variáveis para calcular o resultado numérico.
- Método da Simplificação: Aplica-se a expressões com operações aritméticas, buscando reduzir a expressão a uma forma mais simples e concisa, utilizando as propriedades das operações matemáticas.
- Método da Fatoração: Empregado em expressões algébricas, onde a expressão é decomposta em fatores, simplificando-a e facilitando o cálculo ou análise.
- Método da Equação: Utilizado para resolver equações, encontrando o valor da variável que satisfaz a igualdade.
- Método da Inequação: Desenvolvido para resolver inequações, encontrando o conjunto de valores que satisfazem a desigualdade.
- Método Gráfico: Uma ferramenta visual para representar e analisar soluções de equações e inequações, utilizando gráficos.
- Método Numérico: Empregado para obter aproximações de soluções de expressões complexas que não possuem soluções exatas.
Detalhes das Etapas
A aplicação de cada método envolve etapas específicas. A compreensão dessas etapas é essencial para resolver problemas matemáticos corretamente.
- Método da Substituição: Exemplo: Seja a expressão `2x + 3y`, onde x = 2 e y = 1.
- Substituir x por 2 e y por 1 na expressão: `2
– 2 + 3
– 1` - Calcular: `4 + 3 = 7`
- Resultado: 7
- Substituir x por 2 e y por 1 na expressão: `2
- Método da Simplificação: Exemplo: Simplifique a expressão `5 + 2
– 3 – 1`.- Realizar a multiplicação: `5 + 6 – 1`
- Realizar as somas e subtrações da esquerda para a direita: `11 – 1 = 10`
- Resultado: 10
- Método da Equação: Exemplo: Resolva a equação `2x + 5 = 11`.
- Isolar o termo com a variável: `2x = 11 – 5`
- Calcular: `2x = 6`
- Isolar a variável: `x = 6 / 2`
- Resultado: `x = 3`
Comparação e Contraste
A escolha do método adequado depende da natureza da expressão.
| Método | Vantagens | Desvantagens | Aplicação Recomendada |
|---|---|---|---|
| Substituição | Fácil para valores numéricos conhecidos | Trabalhoso para expressões complexas | Expressões simples com variáveis conhecidas |
| Simplificação | Reduz complexidade | Difícil para múltiplas operações | Expressões aritméticas |
| Fatoração | Simplifica expressões algébricas | Não aplicável a todas as expressões | Expressões algébricas com fatores comuns |
Escolha do Método
A escolha do método depende da complexidade da expressão, do tipo de operação e da presença de variáveis. A necessidade de aproximação também influencia a seleção.
Exemplos com Números Inteiros
Explorando o universo dos números inteiros, mergulharemos em expressões matemáticas que os utilizam. Vamos desvendar os segredos por trás da resolução dessas expressões, aprendendo diferentes métodos e, principalmente, a importância da ordem das operações. Prepare-se para um exercício desafiador e recompensador!
Métodos para Resolver Expressões com Números Inteiros
Para garantir a precisão nos cálculos com números inteiros, a ordem das operações é fundamental. Seguir a ordem correta evita erros e garante resultados confiáveis. Compreender a prioridade das operações (parênteses, expoentes, multiplicação e divisão, adição e subtração) é crucial.
Exemplos de Expressões e Resoluções
Abaixo, apresentamos um quadro com exemplos práticos de expressões matemáticas utilizando apenas números inteiros. Cada exemplo demonstra a aplicação da ordem correta das operações, conduzindo a resultados precisos. Observe atentamente cada etapa da resolução.
| Expressão | Resultado | Etapas de Resolução |
|---|---|---|
| (5 + 3) × 2 – 4 | 10 | 1. (5 + 3) = 8 2. 8 × 2 = 16 3. 16 – 4 = 10 |
| 12 ÷ 3 + 5 × 2 | 14 | 1. 12 ÷ 3 = 4 2. 5 × 2 = 10 3. 4 + 10 = 14 |
| -7 + 15 – 2 × 3 | 1 | 1. 2 × 3 = 6 2. -7 + 15 = 8 3. 8 – 6 = 1 |
| -8 + (-3) × 2 + 10 | -4 | 1. (-3) × 2 = -6 2. -8 + (-6) = -14 3. -14 + 10 = -4 |
Importância da Ordem das Operações
A ordem das operações é crucial para evitar resultados incorretos. Imagine uma receita de bolo: se os ingredientes não forem adicionados na ordem correta, o resultado final pode ser completamente diferente do esperado. Da mesma forma, a ordem das operações em expressões matemáticas garante que o cálculo seja feito de forma precisa e consistente. É como uma regra universal, garantindo resultados consistentes, independente do local ou da pessoa que resolve a expressão.
A ordem das operações (PEMDAS/BODMAS) é fundamental para garantir a precisão nos cálculos com números inteiros.
Exemplos com Frações: Assinale A Alternativa Que Representa Corretamente O Valor Da Seguinte Expressão

Source: z-dn.net
Frações são partes de um todo e estão presentes em inúmeras situações do dia a dia, desde receitas culinárias até cálculos científicos. Compreender as operações com frações é fundamental para a resolução de problemas matemáticos e para o desenvolvimento de habilidades matemáticas. Este tópico detalha diferentes tipos de expressões com frações, apresentando exemplos e passos para resolvê-las.
Tipos de Expressões com Frações
As frações podem ser combinadas em diversas expressões matemáticas. A seguir, estão os principais tipos de expressões envolvendo frações:
- Adição/Subtração de Frações: Envolve a soma ou subtração de frações com denominadores iguais ou diferentes. É essencial encontrar o mínimo múltiplo comum (MMC) dos denominadores para que as frações tenham denominadores iguais antes de efetuar a operação.
- Multiplicação de Frações: Envolve a multiplicação dos numeradores e denominadores. Simplificar as frações antes de realizar a multiplicação pode tornar o cálculo mais simples e eficiente.
- Divisão de Frações: Envolve a multiplicação da primeira fração pelo inverso da segunda. Essa regra simplifica a divisão de frações para a multiplicação, o que é mais direto.
- Frações Mistas: Envolve a combinação de um número inteiro e uma fração. É importante converter frações mistas em frações impróprias para realizar as operações matemáticas.
- Simplificação de Frações: Envolve a redução de uma fração à sua forma mais simples, dividindo o numerador e o denominador por um mesmo fator comum. Essa etapa é crucial para obter a forma mais reduzida e mais fácil de trabalhar com a fração.
- Expressões Combinadas: Envolve a combinação de diferentes operações com frações. A ordem das operações (PEMDAS/BODMAS) deve ser seguida cuidadosamente para obter o resultado correto.
Etapas para Resolução
Para resolver expressões com frações, é necessário seguir etapas específicas, dependendo da operação envolvida:
- Adição/Subtração: Encontre o MMC dos denominadores, converta as frações para denominadores comuns, some ou subtraia os numeradores e simplifique a fração resultante.
- Multiplicação: Multiplique os numeradores e os denominadores, simplifique a fração resultante. Simplificar antes de multiplicar facilita a resolução.
- Divisão: Inverte a segunda fração e multiplique as duas frações. A divisão de frações é equivalente à multiplicação pelo inverso da segunda fração.
- Frações Mistas: Converta a fração mista em fração imprópria, realize as operações com frações impróprias e, se necessário, converta a fração imprópria de volta em fração mista.
Exemplo de Quadro
O quadro a seguir demonstra um exemplo de resolução passo a passo de uma expressão com frações:
| Expressão | Passo 1 | Passo 2 | Passo 3 | Resultado Simplificado |
|---|---|---|---|---|
| 1/2 + 1/3 | Encontrar MMC(2,3) = 6 | Converter frações para denominador comum: (3/6) + (2/6) | Somar os numeradores: 3+2 = 5 | 5/6 |
Propriedade da Simplificação
A propriedade da simplificação de frações é fundamental para obter resultados mais simples e reduzidos. Simplificar frações envolve dividir o numerador e o denominador por um mesmo fator comum, o que não altera o valor da fração.
- Exemplo 1: Simplifique a fração 6/8. Divida o numerador e o denominador por 2, resultando em 3/4.
- Exemplo 2: Simplifique a fração 10/15. Divida o numerador e o denominador por 5, resultando em 2/3.
A aplicação da propriedade da simplificação em expressões combinadas reduz o trabalho e garante resultados precisos.
Exemplos com Decimais

Source: z-dn.net
Números decimais estão presentes em inúmeras situações do nosso cotidiano, desde compras no supermercado até cálculos científicos complexos. Compreender como lidar com essas expressões é crucial para garantir precisão e evitar erros que podem ter consequências significativas. A precisão em cálculos com decimais é fundamental para evitar resultados incorretos que podem gerar prejuízos ou interpretações imprecisas.
Tabela de Exemplos com Decimais
A precisão em cálculos com decimais é fundamental para evitar erros que podem gerar consequências significativas em diversas áreas. Erros em etapas intermediárias de um cálculo podem acumular e levar a resultados completamente diferentes do esperado. Observe como os passos detalhados são cruciais para garantir a exatidão dos resultados.
| Expressão | Passo 1 | Passo 2 | Resultado |
|---|---|---|---|
| (2,5 + 1,75) – 3,2 | 2,5 + 1,75 = 4,25 | 4,25 – 3,2 = 13,6 | 13,6 |
| (5,2 – 1,8) / 0,4 | 5,2 – 1,8 = 3,4 | 3,4 / 0,4 = 8,5 | 8,5 |
| 2,75 – 1,5 + 0,2 | 2,75 – 1,5 = 4,125 | 4,125 + 0,2 = 4,325 | 4,325 |
| 10,5 / 2,1 – 1,2 | 10,5 / 2,1 = 5 | 5 – 1,2 = 3,8 | 3,8 |
| 3,14 – 4,5 | 3,14 – 4,5 = 14,13 | 14,13 | |
| 0,65 + 0,35 – 2 | 0,35 – 2 = 0,7 | 0,65 + 0,7 = 1,35 | 1,35 |
Importância da Precisão
A precisão nos cálculos com decimais é crucial em diversas áreas, desde a engenharia até as finanças. Erros em cálculos com decimais podem levar a problemas significativos. Imagine, por exemplo, a construção de uma ponte. Um pequeno erro nos cálculos com decimais pode levar a uma estrutura instável e perigosa. Em aplicações financeiras, erros em cálculos com decimais podem resultar em perdas financeiras significativas.
Em ciência, a precisão é fundamental para obter resultados confiáveis e evitar interpretações equivocadas. Em todos esses casos, a atenção aos detalhes e a verificação dos cálculos são essenciais para garantir resultados corretos.
Estruturação de Dados
Source: passeidireto.com
Organizar informações de forma clara e eficiente é fundamental para a compreensão e análise de dados, especialmente em matemática. Imagine ter um monte de expressões matemáticas, cada uma com seu resultado. Sem uma estrutura adequada, encontrar a solução desejada seria como procurar uma agulha num palheiro. Neste tópico, vamos aprender a construir tabelas HTML para apresentar exemplos e suas respectivas soluções de forma organizada e responsiva, garantindo que a informação seja acessível e intuitiva em diferentes dispositivos.
Criação de Tabelas HTML
Tabelas HTML são ferramentas poderosas para apresentar dados em formato tabular, permitindo a organização de informações em linhas e colunas. A estrutura de uma tabela permite que você visualize os dados de forma clara e hierárquica, facilitando a comparação e a extração de insights. A utilização de tabelas em páginas web é crucial para a apresentação de resultados de forma organizada e compreensível.
Estrutura da Tabela
Para construir uma tabela responsiva e eficiente, é necessário seguir uma estrutura bem definida, utilizando as tags HTML apropriadas. Isso garante que a tabela seja visualizada corretamente em diferentes dispositivos, como computadores, tablets e smartphones.
| Exemplo | Expressão | Solução | Observações |
|---|---|---|---|
| 1 | 2 + 3 | 5 | Adição simples. |
| 2 | 10 – 4 | 6 | Subtração. |
| 3 | 5 – 2 | 10 | Multiplicação. |
| 4 | 12 / 3 | 4 | Divisão. |
| 5 | (2 + 3) – 2 | 10 | Prioridade de operações. |
Características de uma Tabela Responsiva
Uma tabela responsiva se adapta automaticamente ao tamanho da tela do dispositivo, garantindo que o conteúdo seja apresentado de forma clara e legível. Isso é alcançado através de técnicas de layout que utilizam unidades relativas, como porcentagem, e propriedades CSS que ajustam o tamanho das células da tabela para diferentes resoluções de tela.
- Flexibilidade: A tabela deve se adaptar a diferentes tamanhos de tela, mantendo a clareza e a organização dos dados.
- Legibilidade: A fonte e o espaçamento devem ser adequados para garantir que a tabela seja fácil de ler, mesmo em telas menores.
- Acessibilidade: A tabela deve ser acessível para usuários com deficiência, usando técnicas como descrições alternativas para imagens e legendas para as colunas.
Exemplo Prático
A tabela acima demonstra um exemplo prático de como estruturar dados matemáticos em uma tabela HTML. Observe como cada coluna (Exemplo, Expressão, Solução e Observações) contém informações relevantes, organizadas e fáceis de compreender. A utilização de tags HTML como <table>, <tr> (para linhas) e <td> (para células) é crucial para criar a estrutura tabular.
Representação Visual de Expressões Matemáticas
A visualização gráfica de expressões matemáticas é fundamental para a compreensão de suas propriedades e comportamento. Os gráficos permitem a interpretação visual das relações entre variáveis, facilitando a análise de tendências, pontos importantes e aplicações práticas. Nesta seção, exploraremos como diferentes tipos de gráficos representam diferentes tipos de expressões matemáticas, destacando as características dos gráficos e sua ligação com os elementos da expressão.
Tipos de Gráficos
Os gráficos são ferramentas poderosas para visualizar expressões matemáticas, revelando padrões e relacionamentos entre variáveis. Cada tipo de expressão matemática possui um tipo de gráfico ideal para representar suas características. Equações lineares são representadas por linhas retas, funções quadráticas por parábolas, funções exponenciais por curvas exponenciais e funções trigonométricas por curvas sinusoidais ou semelhantes. A escolha do gráfico apropriado é crucial para uma interpretação precisa.
Domínio e Imagem
O domínio de uma função representa o conjunto de todos os valores possíveis para a variável independente (geralmente x), enquanto a imagem representa o conjunto de todos os valores possíveis para a variável dependente (geralmente y). A visualização gráfica permite a determinação imediata do domínio e imagem de uma função. Por exemplo, a função y = x² tem como domínio todos os números reais e como imagem todos os números reais não negativos, visto que o gráfico não se estende para valores negativos de y.
Interceptos
Os interceptos com os eixos x e y são pontos cruciais na análise gráfica de uma função. O intercepto com o eixo x ocorre quando y = 0, e o intercepto com o eixo y ocorre quando x = 0. A visualização dos interceptos fornece informações valiosas sobre o comportamento da função e suas raízes. Por exemplo, na função y = 2x – 4, o intercepto com o eixo x é x = 2 e o intercepto com o eixo y é y = -4.
Pontos Notáveis
Pontos notáveis, como máximos, mínimos, pontos de inflexão e assíntotas, são pontos críticos que revelam informações essenciais sobre o comportamento da função. A análise gráfica desses pontos é essencial para entender as variações e tendências da função. Por exemplo, na função y = x³
3x, os pontos de inflexão estão em x = ±1, enquanto os máximos e mínimos locais podem ser identificados pelo gráfico.
Escalas e Eixos
A escolha adequada das escalas para os eixos x e y é fundamental para a clareza e precisão do gráfico. Escolhas apropriadas garantem que todas as características da função sejam visíveis e que a representação seja precisa. A escala deve permitir a visualização completa da função, incluindo pontos notáveis e tendências.
Legendas e Rótulos
Legendas claras e precisas para os eixos e um título informativo para o gráfico são essenciais para a compreensão da visualização. Um gráfico sem rótulos e legendas é inutilizável, tornando a interpretação confusa. Por exemplo, “Gráfico da função y = sen(x) no intervalo [0, 2π]” é um título adequado para um gráfico da função seno nesse intervalo.
Precisão
A precisão nos cálculos e na representação gráfica é crucial para uma análise precisa. Valores exatos devem ser utilizados sempre que possível, evitando aproximações que possam distorcer a interpretação. Cálculos precisos garantem que o gráfico represente com exatidão a função.
Exemplos de Expressões
Apresentaremos exemplos de diferentes tipos de expressões matemáticas e seus gráficos correspondentes:
- Equação Linear: y = 2x + 1 (representada por uma linha reta). O gráfico mostrará a inclinação e o intercepto com o eixo y.
- Função Quadrática: y = x²
-4x + 3 (representada por uma parábola). O gráfico exibirá o vértice, os interceptos com os eixos e a concavidade da parábola. - Função Exponencial: y = 2 x (representada por uma curva exponencial). O gráfico mostrará o crescimento ou decaimento exponencial.
- Função Trigonométrica: y = sen(x) (representada por uma curva periódica). O gráfico mostrará oscilações periódicas e os valores máximos e mínimos.
Relação entre a Expressão e o Gráfico, Assinale A Alternativa Que Representa Corretamente O Valor Da Seguinte Expressão
A relação entre os elementos da expressão matemática (coeficientes, expoentes, constantes) e as características do gráfico (inclinação, forma, etc.) é fundamental para a compreensão da função. Por exemplo, a mudança no coeficiente linear de uma equação linear afeta diretamente a inclinação da reta no gráfico.
Aplicação Prática
A representação gráfica de expressões matemáticas possui diversas aplicações práticas. Por exemplo, gráficos de crescimento populacional, gráficos de lucro e custo, gráficos de movimento de objetos e modelos de fenômenos físicos. A análise gráfica permite entender tendências e prever comportamentos.
Ao concluirmos nossa jornada pelo universo das expressões matemáticas, esperamos que você tenha adquirido ferramentas essenciais para enfrentar desafios matemáticos com confiança. Desvendamos as operações, aprendemos a lidar com variáveis e funções, e enfrentamos problemas complexos com estratégias eficazes. Agora, você está pronto para aplicar seus conhecimentos em novos cenários e dominar o poder das expressões matemáticas!
Qual a importância de entender a ordem das operações em expressões com números inteiros?
A ordem das operações (PEMDAS/BODMAS) é fundamental para garantir que todos os cálculos sejam feitos na sequência correta. Ignorá-la pode levar a resultados incorretos e a compreensão equivocada do problema. Ela garante a unicidade da solução.
Como simplificar frações?
Para simplificar uma fração, divida o numerador e o denominador pelo maior fator comum (MDC) entre eles. Isso reduz a fração à sua forma mais simples, mantendo o mesmo valor.
Quais são os erros comuns na avaliação de expressões matemáticas?
Erros comuns incluem: esquecer a ordem das operações, realizar operações na sequência errada, não considerar as propriedades das operações, erros na substituição de variáveis e interpretações ambíguas.
Como resolver expressões com decimais?
Resolva expressões com decimais com a mesma atenção que as expressões inteiras, porém, com precisão na localização das casas decimais durante as operações.





