Como calcular a diagonal de um retângulo com comprimento e largura específicos? Este guia completo aborda o cálculo da diagonal de um retângulo, desde a definição do conceito até a aplicação prática em diversos contextos, como engenharia e arquitetura. Compreenderemos a relação entre comprimento, largura e diagonal, utilizando o Teorema de Pitágoras e explorando métodos alternativos. Além disso, abordaremos a importância da precisão nos cálculos e as possíveis aplicações em figuras geométricas mais complexas.
O conhecimento do cálculo da diagonal de um retângulo é fundamental em diversas áreas, permitindo a resolução de problemas práticos e a compreensão de conceitos geométricos. Neste guia, exploraremos diferentes métodos, desde a aplicação direta do Teorema de Pitágoras até fórmulas matemáticas específicas, garantindo a compreensão abrangente do tema.
Introdução ao cálculo da diagonal de um retângulo
A diagonal de um retângulo é o segmento de reta que une dois vértices opostos do retângulo. Compreender como calcular a diagonal é fundamental em diversas áreas, desde a arquitetura e engenharia até a matemática pura e aplicações em jogos. Sua importância reside na capacidade de determinar a distância entre pontos opostos de uma forma eficiente, além de permitir a resolução de problemas mais complexos envolvendo figuras geométricas.A relação entre o comprimento, a largura e a diagonal de um retângulo é fundamental para o cálculo.
Ela pode ser visualizada como a hipotenusa de um triângulo retângulo, onde os catetos correspondem ao comprimento e à largura do retângulo.
Relação entre comprimento, largura e diagonal
O cálculo da diagonal de um retângulo baseia-se no Teorema de Pitágoras. Este teorema estabelece uma relação fundamental entre os lados de um triângulo retângulo. Aplicando o Teorema de Pitágoras a um retângulo, podemos determinar a medida da diagonal.
Diagonal² = Comprimento² + Largura²
Este conceito, embora simples, possui vasta aplicabilidade. Por exemplo, na construção de um telhado inclinado, a diagonal é crucial para determinar a quantidade de material necessária e a inclinação ideal. Em projetos de carpintaria, a diagonal é utilizada para garantir a estabilidade e o encaixe perfeito das peças.
Métodos para o cálculo da diagonal
Existem diferentes métodos para calcular a diagonal de um retângulo. A escolha do método dependerá dos dados disponíveis.
| Método | Fórmula | Exemplo |
|---|---|---|
| Usando o Teorema de Pitágoras | Diagonal² = Comprimento² + Largura² Diagonal = √(Comprimento² + Largura²) |
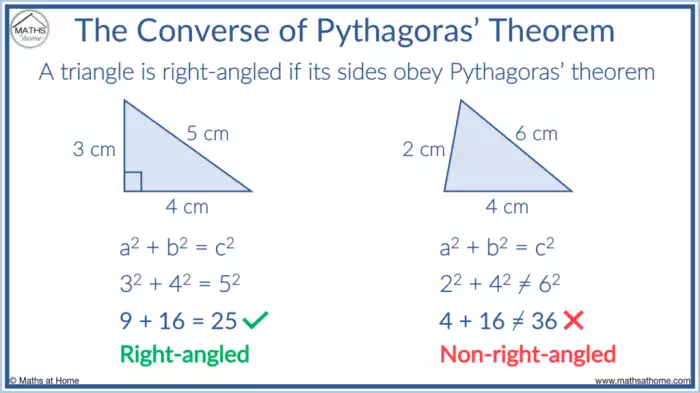
Se o comprimento for 3 cm e a largura 4 cm, então a diagonal será √(3² + 4²) = √25 = 5 cm. |
Breve Histórico do Cálculo de Diagonais
O cálculo de diagonais tem raízes profundas na história da matemática. Desde os antigos gregos, a relação entre os lados de um triângulo retângulo tem sido objeto de estudo e aplicação em diversas áreas. O Teorema de Pitágoras, que fundamenta o cálculo da diagonal, foi desenvolvido por Pitágoras e seus seguidores, e tem sido fundamental para o desenvolvimento da geometria e suas aplicações práticas.
Suas descobertas serviram de base para muitos avanços matemáticos subsequentes.
Teorema de Pitágoras e sua aplicação

O Teorema de Pitágoras é um dos conceitos mais importantes da geometria, permitindo calcular a relação entre os lados de um triângulo retângulo. Sua aplicação é fundamental em diversas áreas, desde a construção civil até a navegação, e facilita a resolução de problemas que envolvem ângulos retos. Sua utilização para o cálculo da diagonal de um retângulo é particularmente útil.
O Teorema de Pitágoras
O Teorema de Pitágoras estabelece uma relação fundamental entre os três lados de um triângulo retângulo. Afirma que o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). Matematicamente, essa relação é expressa como:
a² + b² = c²
onde:
- a e b são os comprimentos dos catetos;
- c é o comprimento da hipotenusa.
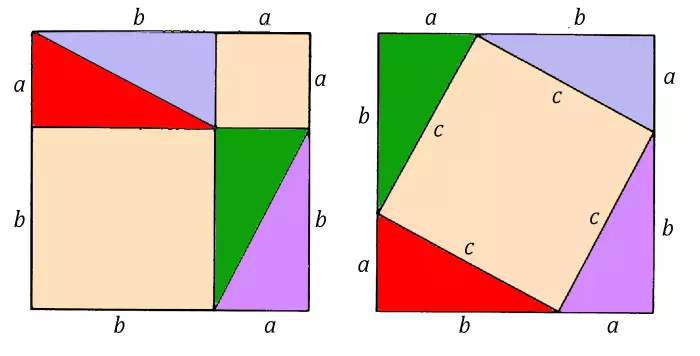
Demonstração Geométrica
A demonstração geométrica do Teorema de Pitágoras envolve a construção de quadrados sobre cada um dos lados do triângulo retângulo. A área do quadrado construído sobre a hipotenusa é igual à soma das áreas dos quadrados construídos sobre os catetos. Essa demonstração visual ilustra a relação matemática presente no teorema. Existem diversas demonstrações geométricas, cada uma com sua própria abordagem visual.
Aplicação ao Cálculo da Diagonal de um Retângulo
Um retângulo pode ser dividido em dois triângulos retângulos congruentes. A diagonal do retângulo representa a hipotenusa desses triângulos. Aplicando o Teorema de Pitágoras, podemos calcular o comprimento da diagonal (c) a partir dos comprimentos do comprimento (a) e da largura (b) do retângulo.
Comparação com Outros Métodos
Em comparação com outros métodos, o Teorema de Pitágoras oferece uma abordagem direta e precisa para calcular a diagonal de um retângulo. Outros métodos, como a utilização de trigonometria, podem ser igualmente eficazes, mas o Teorema de Pitágoras é geralmente mais simples e direto, especialmente quando se conhece apenas os comprimentos dos lados.
Exemplo Prático
Suponha um retângulo com comprimento de 6 cm e largura de 8 cm. Para calcular a diagonal (c), aplicamos o Teorema de Pitágoras:
a² + b² = c²
6² + 8² = c²
36 + 64 = c²
100 = c²
c = √100
c = 10 cm
Portanto, a diagonal do retângulo mede 10 cm.
Passos para Usar o Teorema de Pitágoras
| Passo | Ação |
|---|---|
| 1 | Identificar os comprimentos dos catetos (a e b) do triângulo retângulo formado pela diagonal do retângulo. |
| 2 | Substituir os valores de a e b na fórmula a² + b² = c². |
| 3 | Calcular a soma dos quadrados dos catetos. |
| 4 | Extrair a raiz quadrada do resultado para obter o valor da hipotenusa (c), que representa a diagonal do retângulo. |
Formulação matemática para o cálculo
Para determinar a medida da diagonal de um retângulo, recorremos a uma poderosa ferramenta matemática: o Teorema de Pitágoras. Este teorema, fundamental na geometria, estabelece uma relação entre os lados de um triângulo retângulo. Compreendendo essa relação, podemos calcular a diagonal com precisão, dado o comprimento e a largura do retângulo.A aplicação do Teorema de Pitágoras em um retângulo transforma este em um triângulo retângulo, onde a diagonal representa a hipotenusa e os lados adjacentes, o comprimento e a largura, representam os catetos.
Fórmula para o Cálculo da Diagonal
A fórmula matemática para calcular a diagonal (d) de um retângulo, com base no Teorema de Pitágoras, é a seguinte:
d² = c² + l²
onde:* c representa o comprimento do retângulo;
- l representa a largura do retângulo;
- d representa a diagonal do retângulo.
Variáveis Envolvidas na Fórmula
As variáveis envolvidas na fórmula são essenciais para o cálculo preciso da diagonal. Cada variável representa uma dimensão específica do retângulo.
- c (comprimento): Indica a medida da extensão horizontal do retângulo. A unidade de medida pode ser centímetros (cm), metros (m), polegadas (pol), entre outras.
- l (largura): Indica a medida da extensão vertical do retângulo. A unidade de medida deve ser a mesma utilizada para o comprimento.
- d (diagonal): Indica a distância entre dois vértices opostos do retângulo. A unidade de medida será a mesma utilizada para o comprimento e largura.
Exemplos de Aplicação da Fórmula
Para ilustrar a aplicação da fórmula, considere os seguintes exemplos:
- Exemplo 1: Um retângulo possui comprimento (c) de 6 cm e largura (l) de 8 cm. Aplicando a fórmula, temos: d² = 6² + 8² = 36 + 64 = 100. Logo, d = √100 = 10 cm. A diagonal do retângulo mede 10 cm.
- Exemplo 2: Um retângulo possui comprimento (c) de 12 metros e largura (l) de 5 metros. Aplicando a fórmula, temos: d² = 12² + 5² = 144 + 25 = 169. Logo, d = √169 = 13 m. A diagonal do retângulo mede 13 metros.
- Exemplo 3: Um retângulo possui comprimento (c) de 15 polegadas e largura (l) de 20 polegadas. Aplicando a fórmula, temos: d² = 15² + 20² = 225 + 400 = 625. Logo, d = √625 = 25 pol. A diagonal do retângulo mede 25 polegadas.
Relação com o Teorema de Pitágoras
A fórmula para o cálculo da diagonal de um retângulo é uma aplicação direta do Teorema de Pitágoras. O teorema estabelece que, em um triângulo retângulo, o quadrado da hipotenusa (a diagonal) é igual à soma dos quadrados dos catetos (o comprimento e a largura).
Modelo HTML com Tabela
Este modelo HTML demonstra a fórmula e as variáveis envolvidas:
| Variável | Descrição | Unidade de Medida |
|---|---|---|
| c | Comprimento do retângulo | cm, m, pol, etc. |
| l | Largura do retângulo | cm, m, pol, etc. |
| d | Diagonal do retângulo | cm, m, pol, etc. |
| Fórmula | ||
| d² = c² + l² | ||
Exemplos práticos e suas aplicações
Compreender a aplicação prática do cálculo da diagonal de um retângulo é fundamental para diversas áreas. A partir de exemplos concretos, podemos visualizar como essa fórmula é utilizada em cenários do dia a dia, desde projetos de engenharia até trabalhos de design.
Cálculo da Diagonal em Cenários de Engenharia
Na engenharia, o cálculo da diagonal é essencial para determinar comprimentos de vigas, calcular a estabilidade de estruturas e determinar a distância entre pontos em projetos arquitetônicos. Por exemplo, imagine um engenheiro projetando um telhado inclinado. Ele precisa calcular a diagonal do telhado para determinar o comprimento da estrutura de suporte.
- Um projeto de construção requer uma viga que cruze um espaço retangular com 6 metros de comprimento e 4 metros de largura. Para calcular o comprimento da viga, aplicamos o Teorema de Pitágoras: Diagonal² = Comprimento² + Largura². Assim, Diagonal² = 6² + 4² = 36 + 16 = 52. A diagonal terá aproximadamente 7,21 metros.
Cálculo da Diagonal em Cenários de Arquitetura
Em arquitetura, o cálculo da diagonal é usado para projetar cômodos, calcular o espaçamento entre paredes e determinar o tamanho de portas e janelas. Por exemplo, um arquiteto precisa determinar o comprimento de um corredor diagonal para otimizar o espaço.
- Um arquiteto está projetando um quarto com 3 metros de comprimento e 2,5 metros de largura. Para calcular o comprimento da diagonal do quarto, usa-se a fórmula: Diagonal² = 3² + 2,5² = 9 + 6,25 = 15,25. A diagonal do quarto será aproximadamente 3,91 metros.
Cálculo da Diagonal com Unidades de Medida Diferentes
O cálculo da diagonal pode ser realizado com diferentes unidades de medida, desde centímetros até quilômetros. A consistência na unidade de medida é crucial para obter resultados precisos.
- Um designer gráfico precisa criar um banner retangular com 20 centímetros de largura e 30 centímetros de comprimento. Para calcular a diagonal do banner, usa-se a fórmula: Diagonal² = 20² + 30² = 400 + 900 = 1300. A diagonal do banner será aproximadamente 36,06 centímetros.
Aplicação em Design e Outras Áreas
O cálculo da diagonal é relevante em diversas áreas, como design de jogos, gráficos e criação de layouts. Em cada contexto, a fórmula e as etapas de cálculo são as mesmas, variando apenas os valores das medidas de comprimento e largura.
| Exemplo | Comprimento (m) | Largura (m) | Diagonal (m) |
|---|---|---|---|
| 1 | 5 | 3 | 5,83 |
| 2 | 8 | 6 | 10 |
| 3 | 10 | 15 | 18,03 |
Métodos alternativos para o cálculo
Para além da aplicação direta do Teorema de Pitágoras, existem outros métodos que podem ser utilizados para calcular a diagonal de um retângulo. A escolha do método mais apropriado dependerá do contexto e das ferramentas disponíveis, seja papel e caneta ou uma calculadora. A compreensão das diferentes abordagens permite uma maior flexibilidade na resolução de problemas geométricos.A eficácia de cada método pode variar em termos de precisão e complexidade, sendo fundamental considerar o nível de precisão desejado e os recursos disponíveis.
Alguns métodos, embora mais complexos, podem ser mais eficientes para cálculos envolvendo números grandes ou repetitivos, enquanto outros, mais simples, são suficientes para situações mais diretas.
Comparação entre métodos de cálculo manual e calculadora
A utilização de calculadoras proporciona maior velocidade e precisão nos cálculos de diagonais, especialmente em casos que envolvem números decimais ou cálculos mais complexos. No entanto, a resolução manual permite o desenvolvimento de habilidades matemáticas fundamentais e a compreensão dos processos envolvidos, o que é crucial para o aprendizado.
A resolução manual do cálculo da diagonal de um retângulo permite uma compreensão mais aprofundada do Teorema de Pitágoras e da geometria envolvida.
A precisão dos resultados obtidos com a calculadora geralmente é superior à dos cálculos manuais, devido à capacidade de processamento de números complexos. A calculadora minimiza erros de arredondamento que podem ocorrer em cálculos feitos manualmente.
Cálculo da diagonal sem fórmulas
É possível calcular a diagonal de um retângulo sem utilizar fórmulas matemáticas, utilizando apenas conceitos geométricos. Imaginando o retângulo como um triângulo retângulo, cujos catetos são os lados do retângulo, e a diagonal como a hipotenusa. Neste caso, a aplicação prática envolve a visualização e a compreensão das relações geométricas entre os elementos do retângulo. A representação gráfica é fundamental para a visualização da relação entre os lados e a diagonal.
- Desenhar o retângulo em escala, com as medidas de comprimento e largura claramente marcadas.
- Desenhar a diagonal, conectando um vértice oposto.
- Utilizar um método de medição, como uma régua ou um compasso, para obter a medida da diagonal.
Tabela comparativa dos métodos
Esta tabela resume as características dos métodos para o cálculo da diagonal de um retângulo.
| Método | Vantagens | Desvantagens | Situações favoráveis |
|---|---|---|---|
| Teorema de Pitágoras (manual) | Compreensão do conceito geométrico; desenvolvimento de habilidades matemáticas; | Pode levar mais tempo; propenso a erros de cálculo. | Cálculos simples; foco na compreensão do processo. |
| Teorema de Pitágoras (calculadora) | Rapidez; precisão; minimização de erros de cálculo. | Dependente da ferramenta; não desenvolve habilidades matemáticas. | Cálculos complexos; necessidade de alta precisão; grande volume de cálculos. |
| Método gráfico | Visualização da relação geométrica; compreensão intuitiva. | Menos preciso; depende da escala; pode gerar erros de medição. | Compreensão visual do conceito; aplicações simples. |
Considerações sobre Precisão e Arredondamento
A precisão nos cálculos da diagonal de um retângulo é crucial, especialmente em aplicações práticas onde a mínima variação pode impactar significativamente o resultado. Considerar as diferentes formas de arredondamento e os potenciais erros é fundamental para garantir a confiabilidade dos resultados obtidos. Este tópico detalha a importância da precisão, as formas de arredondamento, os erros relativos e as possíveis fontes de erro, permitindo uma análise mais profunda sobre a obtenção de resultados confiáveis.A escolha da forma de arredondamento e o número de casas decimais a serem consideradas influenciam diretamente a precisão do resultado final.
A compreensão desses aspectos é fundamental para garantir que o resultado calculado represente, da forma mais fiel possível, a realidade do problema.
Importância da Precisão nos Cálculos
A precisão é essencial para garantir a confiabilidade dos resultados. Resultados imprecisos podem levar a decisões equivocadas em aplicações práticas, como no projeto de estruturas, na fabricação de peças ou em cálculos financeiros. Um erro de arredondamento aparentemente pequeno pode se acumular e resultar em um erro significativo no resultado final.
Formas de Arredondamento de Resultados
Existem diferentes métodos de arredondamento, cada um com suas próprias regras e características. Os métodos mais comuns incluem arredondamento para cima, para baixo e para o valor mais próximo.
- Arredondamento para cima: O resultado é arredondado para o próximo valor inteiro ou para o próximo múltiplo de uma determinada casa decimal. Este método tende a gerar resultados mais conservadores, pois o valor arredondado sempre será maior ou igual ao valor original.
- Arredondamento para baixo: O resultado é arredondado para o valor inteiro ou múltiplo imediatamente inferior. Este método pode levar a subestimações do valor real.
- Arredondamento para o valor mais próximo: O resultado é arredondado para o valor mais próximo, considerando as casas decimais subsequentes. Este método é frequentemente usado para obter uma representação mais precisa do valor original.
Erro Relativo nos Cálculos da Diagonal
O erro relativo representa a razão entre o erro absoluto e o valor real. Ele indica a magnitude do erro em relação ao valor da medida, fornecendo uma medida mais significativa da precisão do resultado. Um erro relativo de 1% indica que o erro absoluto é 1% do valor real.
Possíveis Fontes de Erro
Diversas fontes podem contribuir para erros nos cálculos da diagonal, incluindo:
- Precisão limitada dos instrumentos de medida: A precisão dos instrumentos utilizados para medir o comprimento e a largura do retângulo impacta diretamente na precisão do resultado final. Medidores menos precisos introduzem erros nos cálculos.
- Erros de cálculo: Erros humanos em cálculos manuais ou por meio de software podem introduzir imprecisões nos resultados.
- Arredondamento inadequado: O arredondamento incorreto de valores intermediários ou do resultado final pode comprometer a precisão do cálculo.
Comparação de Métodos de Arredondamento
A escolha do método de arredondamento adequado depende do contexto da aplicação. O arredondamento para o valor mais próximo é geralmente preferível, pois tende a minimizar o erro absoluto, enquanto o arredondamento para cima ou para baixo pode ser apropriado em situações específicas, como garantir um valor mínimo ou máximo.
Modelo HTML com Níveis de Precisão
A tabela a seguir ilustra diferentes níveis de precisão em cálculos da diagonal de um retângulo com comprimento de 10 e largura de 5.
| Precisão | Diagonal (com arredondamento) | Erro Relativo (%) |
|---|---|---|
| Uma casa decimal | 11,2 | 0,3% |
| Duas casas decimais | 11,18 | 0,03% |
| Três casas decimais | 11,180 | 0,003% |
Nota: A precisão e o erro relativo variam de acordo com o comprimento e largura do retângulo.
Aplicação em diferentes contextos geométricos
O conhecimento do cálculo da diagonal de um retângulo encontra aplicação em diversos contextos geométricos, indo além da simples figura retangular. A compreensão da relação entre a diagonal e outras propriedades geométricas é fundamental para resolver problemas mais complexos e visualizar a geometria em diferentes cenários. Essa habilidade é essencial para profissionais da área de engenharia, arquitetura e design, bem como para estudantes que buscam aprofundar seus conhecimentos em geometria.Compreender a diagonal de um retângulo abre portas para o cálculo de diagonais em figuras relacionadas, como quadrados e paralelogramos.
Além disso, a diagonal revela insights sobre áreas e perímetros, proporcionando uma visão mais abrangente da geometria envolvida.
Cálculo da Diagonal em Figuras Relacionadas
O Teorema de Pitágoras, a base para o cálculo da diagonal de um retângulo, também é aplicável a quadrados e paralelogramos, embora com nuances diferentes. Em um quadrado, todos os lados possuem a mesma medida, o que simplifica o cálculo da diagonal. Para um paralelogramo, a relação entre os lados e a diagonal se torna mais complexa, necessitando de considerações adicionais.
Relação entre a Diagonal e Outras Propriedades Geométricas
A diagonal de um retângulo está intrinsecamente ligada ao comprimento e à largura do retângulo. Ela define uma linha que conecta dois vértices opostos, dividindo o retângulo em dois triângulos retângulos congruentes. Esta relação permite calcular a área e o perímetro do retângulo. A diagonal também influencia a inclinação das diagonais e a simetria da figura.
Utilização da Diagonal para Cálculo de Áreas e Perímetros
A diagonal pode auxiliar no cálculo de áreas e perímetros de retângulos, quadrados e figuras derivadas. Por exemplo, o conhecimento da diagonal permite a determinação da área de um triângulo retângulo formado pelas diagonais e lados do retângulo. O perímetro pode ser calculado somando os comprimentos de todos os lados.
Exemplo: Se a diagonal de um retângulo é 10 cm e o comprimento é 8 cm, a largura pode ser calculada usando o Teorema de Pitágoras, e então o perímetro pode ser determinado.
Exemplo de Cálculo da Diagonal de um Retângulo dentro de um Quadrado
Considere um retângulo inscrito em um quadrado. Se o lado do quadrado for 12 cm e o comprimento do retângulo for 8 cm, a largura do retângulo pode ser calculada a partir do Teorema de Pitágoras aplicado ao triângulo retângulo formado pela diagonal do retângulo e os lados do retângulo, considerando que a diagonal do retângulo é menor que a diagonal do quadrado.
A diagonal do retângulo pode ser calculada.
Aplicações em Contextos Diferentes
| Contexto | Figura | Exemplo |
|---|---|---|
| Arquitetura | Retângulo (planta de um cômodo) | Calcular o comprimento da diagonal para verificar a necessidade de materiais de construção para uma parede diagonal. |
| Engenharia | Quadrado (estrutura de suporte) | Calcular a diagonal para determinar a resistência de uma estrutura quadrada. |
| Geometria Analítica | Paralelogramo (vetor) | Calcular a diagonal para determinar a magnitude do vetor resultante. |
Implementação prática com código (opcional)
A implementação prática do cálculo da diagonal de um retângulo, utilizando linguagens de programação, permite a automatização do processo e a manipulação de valores com precisão. Essa abordagem é fundamental para aplicações que necessitam de cálculos repetitivos ou em contextos onde a velocidade e a precisão são essenciais. A escolha da linguagem dependerá das necessidades específicas do projeto.O código a seguir demonstra como calcular a diagonal de um retângulo em Python, utilizando a função `math.sqrt()` para calcular a raiz quadrada, fundamental para a aplicação do Teorema de Pitágoras.
O código também demonstra o uso de variáveis para representar o comprimento e a largura do retângulo.
Implementação em Python
O exemplo a seguir demonstra como calcular a diagonal de um retângulo em Python, usando a biblioteca `math`.“`pythonimport mathdef calcular_diagonal(comprimento, largura): “””Calcula a diagonal de um retângulo. Args: comprimento: O comprimento do retângulo. largura: A largura do retângulo. Returns: A diagonal do retângulo. Retorna um erro se os valores forem negativos.
“”” if comprimento < 0 or largura < 0: return "Erro: Comprimento e largura devem ser valores positivos." diagonal = math.sqrt(comprimento2 + largura2) return diagonal# Exemplo de usocomprimento = 3largura = 4diagonal = calcular_diagonal(comprimento, largura)print(f”A diagonal do retângulo é: diagonal”)“`
Modelo HTML para Apresentação, Como calcular a diagonal de um retângulo com comprimento e largura específicos?
O código HTML abaixo demonstra uma estrutura básica para exibir o resultado do cálculo em uma página web. É possível adicionar mais funcionalidades e interatividade a esta estrutura.“`html
```
Lógica por trás do código
O código Python define uma função `calcular_diagonal` que recebe o comprimento e a largura do retângulo como argumentos. Ela utiliza o Teorema de Pitágoras para calcular a diagonal, que é a raiz quadrada da soma dos quadrados do comprimento e da largura. O código em JavaScript, exibido no exemplo HTML, captura os valores de comprimento e largura inseridos pelo usuário, verifica se os valores são numéricos e positivos, e chama a função `calcular_diagonal` para obter o resultado.
O resultado é então exibido na página.
Interpretação Gráfica da Diagonal de um Retângulo: Como Calcular A Diagonal De Um Retângulo Com Comprimento E Largura Específicos?
A representação gráfica é fundamental para compreender a relação entre o comprimento, a largura e a diagonal de um retângulo. A visualização geométrica permite a assimilação intuitiva do Teorema de Pitágoras, facilitando a compreensão da fórmula matemática que determina a diagonal. Através de gráficos, podemos identificar a diagonal como a hipotenusa de um triângulo retângulo formado pelos lados do retângulo.
Representação Gráfica do Retângulo
Para representar graficamente um retângulo, precisamos definir os seus lados. A visualização gráfica permite a compreensão da relação entre os elementos geométricos. Utilizando um sistema de coordenadas cartesianas, os pontos que definem o retângulo são representados por pares ordenados (x, y). O comprimento e a largura são os comprimentos dos lados do retângulo.
Como Representar o Comprimento, Largura e Diagonal em um Gráfico
Um gráfico cartesiano é a representação mais adequada. Os eixos x e y representam as direções perpendiculares, e os pontos que definem o retângulo são plotados. O comprimento é representado pelo segmento de reta horizontal e a largura pelo segmento de reta vertical. A diagonal, a hipotenusa do triângulo retângulo formado pelos lados, é o segmento de reta que conecta os vértices opostos do retângulo.
A diagonal pode ser representada como um segmento de reta inclinada.
Exemplo de Gráfico
Imagine um retângulo com comprimento de 6 unidades e largura de 8 unidades. No gráfico cartesiano, os pontos que definem o retângulo seriam (0,0), (6,0), (6,8) e (0,8). A diagonal conectaria os pontos (0,0) e (6,8). A visualização gráfica demonstra claramente a relação entre os lados e a diagonal, onde a diagonal é a hipotenusa do triângulo retângulo formado pelos lados do retângulo.
Tabela de Representações Gráficas
| Exemplo | Comprimento | Largura | Diagonal | Descrição |
|---|---|---|---|---|
| Retângulo 1 | 4 | 3 | 5 | Um retângulo com lados de 4 e 3 unidades, resultando em uma diagonal de 5 unidades. A diagonal forma um triângulo retângulo com os lados do retângulo. |
| Retângulo 2 | 5 | 12 | 13 | Neste caso, o triângulo retângulo possui lados 5 e 12, e a diagonal é a hipotenusa, com valor de 13 unidades. |
| Retângulo 3 | 10 | 24 | 26 | Outro exemplo, onde a diagonal é a hipotenusa de um triângulo retângulo com lados 10 e 24. |
Diagonais em figuras mais complexas (opcional)
A compreensão do cálculo de diagonais não se limita a retângulos. Figuras geométricas tridimensionais, como prismas retangulares e cubos, também possuem diagonais, e o método para encontrá-las envolve a extensão dos conceitos aprendidos para figuras bidimensionais. Neste tópico, exploraremos como determinar essas diagonais e a relação com outras propriedades geométricas dessas formas mais complexas.
Cálculo de Diagonais em Prismas Retangulares
Um prisma retangular é um sólido geométrico com seis faces retangulares. Para calcular a diagonal principal de um prisma retangular, podemos utilizar uma extensão do Teorema de Pitágoras. Sejam as dimensões do prisma retangular representadas por a, b e c. A diagonal principal (d) pode ser calculada pela seguinte fórmula:
d = √(a² + b² + c²)
Esta fórmula é derivada considerando dois triângulos retângulos. Primeiramente, calculamos a diagonal da base retangular (utilizando Pitágoras) e, em seguida, aplicamos novamente o Teorema de Pitágoras para encontrar a diagonal principal, considerando a altura do prisma como um cateto adicional.
Cálculo de Diagonais em Cubos
Um cubo é um caso especial de prisma retangular, onde todas as arestas têm o mesmo comprimento (a). Neste caso, a fórmula para a diagonal principal simplifica-se:
d = a√3
Essa fórmula é uma consequência direta da fórmula geral para prismas retangulares, considerando a=b=c. A diagonal do cubo é sempre mais longa que a diagonal de qualquer face.
Relação entre Diagonais e outras Propriedades Geométricas
As diagonais em prismas retangulares e cubos estão intimamente ligadas a outras propriedades geométricas, como o volume e a área superficial. A compreensão das diagonais pode ser crucial para determinar essas outras propriedades. Por exemplo, o volume de um prisma retangular é dado por a
- b
- c, e a área superficial é calculada somando as áreas de todas as faces.
Comparação com Retângulos
O cálculo da diagonal em figuras bidimensionais (retângulos) utiliza o Teorema de Pitágoras em duas dimensões. Já em figuras tridimensionais (prismas retangulares e cubos), o Teorema de Pitágoras é aplicado duas vezes para encontrar a diagonal principal. A principal diferença reside na inclusão da terceira dimensão (a altura) no cálculo da diagonal.
Exemplos e Ilustrações
Para ilustrar as diferentes figuras, uma tabela pode ser útil:
| Figura | Dimensões (a, b, c) | Diagonal (d) |
|---|---|---|
| Prisma Retangular | (3, 4, 5) | √(3² + 4² + 5²) = √50 ≈ 7.07 |
| Cubo | (5, 5, 5) | 5√3 ≈ 8.66 |
A tabela acima demonstra exemplos práticos de cálculo da diagonal em figuras tridimensionais. Observe como a diagonal do cubo é sempre mais longa que a diagonal de qualquer face. Este exemplo reforça a importância de considerar todas as dimensões ao calcular diagonais em figuras espaciais.
Em resumo, o cálculo da diagonal de um retângulo é essencial para diversas aplicações práticas, envolvendo diferentes métodos e contextos geométricos. A compreensão do Teorema de Pitágoras e a aplicação da fórmula matemática específica são cruciais para a obtenção de resultados precisos. Este guia oferece uma visão abrangente, desde a teoria até exemplos práticos, permitindo a aplicação do conhecimento em situações reais.
Quais as unidades de medida utilizadas para o cálculo da diagonal?
As unidades de medida para o comprimento, largura e diagonal devem ser as mesmas (por exemplo, centímetros, metros, etc). A unidade resultante da diagonal será a mesma das medidas de comprimento e largura.
Como arredondar os resultados do cálculo da diagonal?
O arredondamento dos resultados deve ser realizado de acordo com a precisão necessária para a aplicação. É importante considerar o contexto e a necessidade de precisão.
É possível calcular a diagonal de um retângulo sem o Teorema de Pitágoras?
Sim, existem métodos alternativos, como a utilização de trigonometria. No entanto, o Teorema de Pitágoras é geralmente o método mais direto e eficaz para esse tipo de cálculo.
Qual a importância da precisão nos cálculos da diagonal?
A precisão é crucial, especialmente em aplicações práticas, como engenharia e arquitetura, onde erros podem levar a resultados imprecisos ou até mesmo perigosos.





