Como calcular a diagonal de um retângulo sem usar calculadora? Este guia apresenta métodos práticos e eficientes para determinar o comprimento da diagonal de um retângulo, utilizando o Teorema de Pitágoras e técnicas alternativas, sem a necessidade de uma calculadora. Aprenda a realizar esses cálculos de forma precisa e passo a passo, explorando diferentes exemplos e simplificações.
Compreender como calcular a diagonal de um retângulo é fundamental em diversas áreas, desde a geometria até aplicações práticas em projetos de construção e engenharia. Este conteúdo irá abordar os conceitos básicos, fornecer exemplos práticos e discutir as simplificações possíveis para facilitar os cálculos manuais.
Introdução ao conceito de diagonal de um retângulo
A diagonal de um retângulo é um segmento de reta que une dois vértices opostos do retângulo. Esta linha imaginária desempenha um papel fundamental na geometria e em diversas aplicações práticas, como em arquitetura, engenharia e até mesmo em jogos. Compreender a relação entre os lados e a diagonal de um retângulo é essencial para resolver problemas geométricos e para calcular áreas e perímetros de figuras compostas.A diagonal de um retângulo cria um triângulo retângulo com os lados do retângulo, o que nos permite utilizar o Teorema de Pitágoras para encontrar o comprimento da diagonal.
Esta relação fundamental simplifica cálculos e permite uma compreensão mais profunda da geometria dos retângulos.
Definição da Diagonal de um Retângulo
Uma diagonal de um retângulo é um segmento de reta que liga dois vértices opostos do retângulo. Graficamente, representa-se a diagonal como uma linha que cruza o retângulo, conectando um canto ao canto oposto. A diagonal divide o retângulo em dois triângulos retângulos congruentes.
Relação entre os Lados e a Diagonal de um Retângulo
O Teorema de Pitágoras estabelece a relação fundamental entre os lados e a diagonal de um retângulo. Para um retângulo com lados de comprimento ‘a’ e ‘b’, e diagonal ‘d’, o teorema afirma que:
d2 = a 2 + b 2
Essa relação demonstra que o quadrado da diagonal é igual à soma dos quadrados dos lados. Por exemplo, se um retângulo possui lados de 3 cm e 4 cm, a diagonal terá um comprimento de √(3 2 + 4 2) = √25 = 5 cm.
Importância do Conhecimento da Diagonal em Geometria
O conhecimento da diagonal é crucial para calcular áreas de figuras compostas por retângulos ou para determinar o perímetro de um retângulo. Além disso, a compreensão da relação entre os lados e a diagonal permite a aplicação do Teorema de Pitágoras em problemas mais complexos de geometria. Por exemplo, em construções, a diagonal de um terreno retangular pode ser usada para determinar a distância entre dois pontos opostos.
Um Pequeno Histórico da Descoberta da Diagonal de um Retângulo
A compreensão da relação entre os lados e a diagonal de um retângulo remonta aos antigos matemáticos gregos, particularmente Pitágoras e seus seguidores. O Teorema de Pitágoras, que estabelece essa relação, é um dos teoremas mais fundamentais da geometria e tem sido utilizado ao longo da história em diversas áreas, desde a arquitetura até a astronomia. A descoberta desta relação contribuiu significativamente para o desenvolvimento da geometria e da matemática como um todo.
Diagrama de um Retângulo com sua Diagonal
Imagine um retângulo ABCD. Os lados AB e BC medem ‘a’ e ‘b’, respectivamente. A diagonal AC liga os vértices A e C. Este diagrama ilustra visualmente a diagonal do retângulo e sua relação com os lados.
[Aqui seria o diagrama do retângulo com a diagonal, que não posso criar visualmente.]
O diagrama mostraria o retângulo ABCD, com os lados AB e BC, e a diagonal AC, que conecta os vértices A e C. Os ângulos internos do retângulo seriam todos de 90 graus.
Teorema de Pitágoras
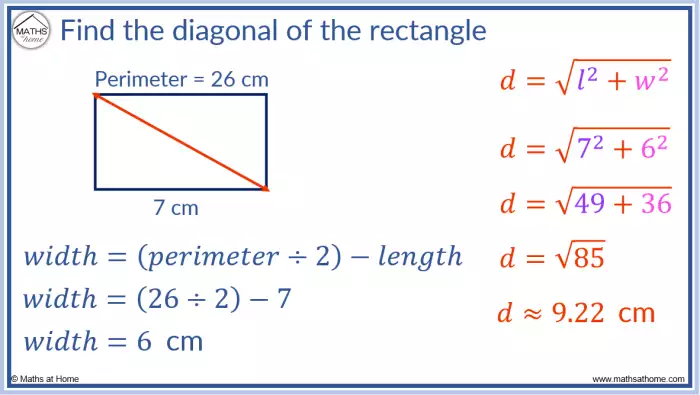
O Teorema de Pitágoras é um princípio fundamental da geometria que estabelece uma relação entre os lados de um triângulo retângulo. Sua aplicação é vasta, abrangendo desde cálculos de distâncias até a resolução de problemas de engenharia e arquitetura. Compreendê-lo é essencial para determinar a diagonal de um retângulo, pois ele fornece uma fórmula direta para esse cálculo.O Teorema de Pitágoras descreve a relação entre os catetos (lados que formam o ângulo reto) e a hipotenusa (lado oposto ao ângulo reto) de um triângulo retângulo.
Esta relação permite determinar o comprimento de um lado desconhecido, se os outros dois forem conhecidos.
Formulação Matemática
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Matematicamente, isso é expresso como:
a² + b² = c²
onde:
- a e b representam os comprimentos dos catetos;
- c representa o comprimento da hipotenusa.
Aplicação ao Cálculo da Diagonal de um Retângulo
Para calcular a diagonal de um retângulo, podemos utilizar o Teorema de Pitágoras. Imagine um retângulo. Se traçarmos uma diagonal, dividimos o retângulo em dois triângulos retângulos congruentes. Os lados do retângulo correspondem aos catetos do triângulo, e a diagonal corresponde à hipotenusa.
Passos para Aplicação do Teorema
- Identifique os comprimentos dos lados do retângulo (catetos). Chame-os de ‘a’ e ‘b’.
- Substitua os valores de ‘a’ e ‘b’ na fórmula de Pitágoras: a² + b² = c².
- Calcule a soma dos quadrados dos catetos (a² + b²).
- Calcule a raiz quadrada do resultado obtido no passo anterior para encontrar o valor de ‘c’ (diagonal).
Exemplo Prático
Suponha um retângulo com lados medindo 3 cm e 4 cm. Aplicando o Teorema de Pitágoras:
- a = 3 cm
- b = 4 cm
- a² + b² = 3² + 4² = 9 + 16 = 25
- c² = 25
- c = √25 = 5 cm
Portanto, a diagonal do retângulo mede 5 cm.
Comparação de Triângulos Retângulos
A tabela abaixo demonstra a relação entre os lados de diferentes triângulos retângulos.
| Cateto a | Cateto b | Hipotenusa c |
|---|---|---|
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 6 | 8 | 10 |
| 7 | 24 | 25 |
Cálculo da Diagonal sem Calculadora
Para determinar a medida da diagonal de um retângulo sem recorrer a uma calculadora, métodos alternativos podem ser empregados. Esses métodos, baseados em princípios matemáticos como o Teorema de Pitágoras, permitem cálculos precisos, mesmo sem a utilização de instrumentos eletrônicos. A escolha do método mais adequado dependerá das dimensões dos lados do retângulo.A eficácia dos métodos alternativos para o cálculo da diagonal de um retângulo sem calculadora é afetada principalmente pela natureza dos comprimentos dos lados do retângulo.
Para lados com valores mais complexos ou não-inteiros, os métodos que envolvem decomposição ou aproximações podem se tornar mais vantajosos, enquanto métodos mais diretos são mais eficazes para lados com valores inteiros e/ou com padrões de fácil manipulação mental.
Métodos para Cálculo da Diagonal Sem Calculadora
Os métodos apresentados a seguir permitem o cálculo da diagonal de um retângulo sem a utilização de calculadora, utilizando apenas operações aritméticas básicas.
-
Utilizando o Teorema de Pitágoras: Este método é o mais direto e eficaz para a maioria dos casos. O Teorema de Pitágoras estabelece que, em um triângulo retângulo, o quadrado da hipotenusa (diagonal do retângulo) é igual à soma dos quadrados dos catetos (lados do retângulo).
c² = a² + b²
onde:
- c representa a diagonal
- a e b representam os lados do retângulo
- Decomposição em Números Redondos: Para lados com valores que permitem decomposição em números redondos, pode-se facilitar o cálculo. Ao decompor os lados em números mais simples, facilita-se a obtenção da diagonal.
- Método da Aproximação: Para lados com valores não inteiros, ou quando se deseja uma aproximação, podem-se utilizar aproximações racionais dos números para simplificar o cálculo.
Exemplo Prático com o Teorema de Pitágoras
Suponha um retângulo com lados medindo 3 cm e 4 cm. Para calcular a diagonal (c), aplicamos o Teorema de Pitágoras:
| Etapa | Cálculo |
|---|---|
| 1. Calcular o quadrado dos lados | 3² = 9 cm² e 4² = 16 cm² |
| 2. Somar os quadrados dos lados | 9 cm² + 16 cm² = 25 cm² |
| 3. Calcular a raiz quadrada da soma | √25 cm² = 5 cm |
| Resultado | A diagonal do retângulo mede 5 cm. |
Exemplos práticos com diferentes valores
Para consolidar o entendimento do cálculo da diagonal de um retângulo sem calculadora, vamos explorar alguns exemplos práticos com diferentes medidas para os lados. Cada exemplo detalhará os passos do cálculo, demonstrando como arredondar os resultados para valores racionais e a importância da precisão nos cálculos.Para esses exemplos, utilizaremos o Teorema de Pitágoras, que estabelece a relação entre os lados de um triângulo retângulo.
A diagonal de um retângulo pode ser vista como a hipotenusa de um triângulo retângulo formado pelos lados do retângulo.
Cálculos da Diagonal em Diferentes Retângulos
Aplicando o Teorema de Pitágoras, podemos calcular a diagonal de um retângulo qualquer. A fórmula é: d² = a² + b², onde ‘d’ é a diagonal, e ‘a’ e ‘b’ são os lados do retângulo.
- Exemplo 1: Um retângulo com lados medindo 3 cm e 4 cm.
Aplicando a fórmula: d² = 3² + 4² = 9 + 16 = 25.
Para encontrar a diagonal ‘d’, calculamos a raiz quadrada de 25, resultando em d = 5 cm. Este é um exemplo simples, onde a diagonal é um valor inteiro.
- Exemplo 2: Um retângulo com lados medindo 6 cm e 8 cm.
Aplicando a fórmula: d² = 6² + 8² = 36 + 64 = 100.
A raiz quadrada de 100 é 10, então d = 10 cm.
- Exemplo 3: Um retângulo com lados medindo 5 cm e 12 cm.
Aplicando a fórmula: d² = 5² + 12² = 25 + 144 = 169.
A raiz quadrada de 169 é 13, então d = 13 cm.
- Exemplo 4: Um retângulo com lados medindo 7 cm e 9 cm.
Aplicando a fórmula: d² = 7² + 9² = 49 + 81 = 130.
A raiz quadrada de 130 é aproximadamente 11,40. Neste caso, arredondamos para 11,4 cm. A precisão do arredondamento depende da necessidade do problema.
Tabela de Exemplos de Retângulos e Suas Diagonais
A tabela a seguir resume os exemplos acima, fornecendo uma visão geral dos cálculos e resultados. A precisão nos cálculos é fundamental para garantir a acurácia dos resultados.
| Lado a (cm) | Lado b (cm) | Diagonal d (cm) |
|---|---|---|
| 3 | 4 | 5 |
| 6 | 8 | 10 |
| 5 | 12 | 13 |
| 7 | 9 | 11,40 (aproximado) |
Ilustrações e representações visuais: Como Calcular A Diagonal De Um Retângulo Sem Usar Calculadora?
Compreender a diagonal de um retângulo torna-se mais fácil com a ajuda de representações visuais. Imagens e diagramas podem esclarecer a relação entre os lados do retângulo e sua diagonal, além de ilustrar a aplicação do Teorema de Pitágoras. Essas representações facilitam a compreensão do conceito e tornam o cálculo mais intuitivo.A visualização é fundamental para a assimilação do conceito de diagonal de um retângulo.
Ao visualizar um retângulo com sua diagonal, podemos observar como ela conecta dois vértices opostos e forma um triângulo retângulo com os lados do retângulo.
Representação Gráfica de um Retângulo
Um retângulo é um quadrilátero com quatro ângulos retos. Para ilustrar a diagonal, imagine um retângulo ABCD, onde os lados AB e BC são perpendiculares. A diagonal AC conecta os vértices A e C. A diagonal divide o retângulo em dois triângulos retângulos congruentes. A figura destaca a relação entre os lados do retângulo (catetos) e a diagonal (hipotenusa).
Componentes de um Retângulo
Um retângulo possui quatro lados e quatro ângulos. Os lados opostos são paralelos e congruentes. Os ângulos internos são todos retos (90 graus). A diagonal conecta dois vértices opostos do retângulo.
Relação com o Teorema de Pitágoras
O Teorema de Pitágoras é essencial para calcular a diagonal de um retângulo. Ele estabelece a relação entre os lados e a hipotenusa de um triângulo retângulo. No caso do retângulo, os lados do retângulo são os catetos, e a diagonal é a hipotenusa do triângulo retângulo formado pela diagonal e os dois lados adjacentes. A fórmula do Teorema de Pitágoras é:
hipotenusa² = cateto² + cateto²
Onde a hipotenusa representa a diagonal, e os catetos representam os lados do retângulo.
Importância da Visualização
A visualização de um retângulo com sua diagonal facilita a compreensão da aplicação do Teorema de Pitágoras. A imagem ajuda a identificar os elementos relevantes (lados e diagonal) e a relação entre eles. Essa visualização facilita a dedução da fórmula para o cálculo da diagonal.
Diagrama de Cálculo Passo a Passo, Como calcular a diagonal de um retângulo sem usar calculadora?
O diagrama abaixo demonstra os passos para calcular a diagonal de um retângulo com lados de 3 cm e 4 cm.
| Passo | Ação | Cálculo |
|---|---|---|
| 1 | Identificar os lados do retângulo (catetos). | lado1 = 3 cm, lado2 = 4 cm |
| 2 | Aplicar o Teorema de Pitágoras. | diagonal² = lado1² + lado2² |
| 3 | Substituir os valores dos lados na fórmula. | diagonal² = 3² + 4² = 9 + 16 = 25 |
| 4 | Calcular a raiz quadrada de ambos os lados. | diagonal = √25 = 5 cm |
| 5 | Resultado final. | A diagonal do retângulo é 5 cm. |
Aplicações práticas da diagonal em situações reais
A diagonal, um conceito geométrico fundamental, apresenta aplicações práticas em diversas áreas, desde a construção civil até a solução de problemas do dia a dia. Compreender como calcular a diagonal permite otimizar projetos, reduzir custos e garantir precisão em medidas. A sua aplicação vai além da matemática pura, impactando diretamente em soluções de engenharia e planejamento.O cálculo da diagonal é crucial em situações onde é necessário determinar a distância mais curta entre dois pontos em um retângulo ou forma semelhante.
A aplicação do Teorema de Pitágoras, como vimos anteriormente, é a base para este cálculo, permitindo encontrar a diagonal sem o uso de instrumentos complexos. Isto torna o cálculo acessível e prático para uma ampla gama de situações.
Exemplos de utilização em construções
A diagonal é fundamental em projetos de construção, especialmente em estruturas como telhados, paredes e pisos. A determinação da inclinação, o cálculo de vigas e o posicionamento preciso de materiais dependem frequentemente da diagonal. A compreensão do seu cálculo facilita o projeto e a execução de tarefas complexas.
- Telhados inclinados: A inclinação de um telhado é determinada pela diagonal do triângulo formado pelo comprimento da cobertura e a altura da inclinação. O cálculo da diagonal permite determinar a quantidade de material necessária para o telhado, a posição correta das telhas e a estabilidade da estrutura. A precisão no cálculo garante a segurança e a durabilidade do telhado.
- Construção de paredes: Na construção de paredes, a diagonal é usada para garantir que a estrutura esteja alinhada e vertical. O uso de um nível e o cálculo da diagonal podem auxiliar na verificação da perpendicularidade das paredes e na detecção de desvios, garantindo a estabilidade e a estética da obra.
- Planejamento de pisos: A diagonal pode ser utilizada no planejamento de pisos, permitindo a determinação do tamanho de ladrilhos ou pisos para garantir um alinhamento preciso e a cobertura completa da área.
Situações da vida real onde o cálculo é útil
O cálculo da diagonal encontra aplicações práticas em diversas situações do dia a dia, além das construções.
- Encontrar a distância mais curta entre dois pontos: Imagine que você precisa atravessar um terreno retangular. A diagonal representa a distância mais curta entre os pontos opostos, facilitando a escolha do melhor caminho. Esta aplicação pode ser utilizada para determinar a melhor rota em mapas ou em espaços confinados.
- Construção de móveis: A diagonal de um móvel pode ser útil para garantir que a estrutura esteja alinhada e tenha as medidas corretas. O cálculo da diagonal ajuda na construção de móveis, como mesas, camas e armários, garantindo precisão e estabilidade.
- Diagnóstico de problemas em estruturas: A diagonal pode ajudar a identificar se uma estrutura, como um piso ou um móvel, está deformada. A comparação da diagonal medida com a diagonal teórica pode revelar problemas estruturais e permitir intervenções preventivas.
Cálculo da diagonal de um telhado inclinado
Considere um telhado com comprimento de 10 metros e altura de 2 metros. Para calcular a diagonal, utilizamos o Teorema de Pitágoras:
d² = c² + h²
onde:
- d = diagonal (comprimento da inclinação do telhado)
- c = comprimento da base do telhado (10 metros)
- h = altura do telhado (2 metros)
Substituindo os valores:
d² = 10² + 2² = 100 + 4 = 104
d = √104 ≈ 10,2 metros
Portanto, a diagonal do telhado é aproximadamente 10,2 metros.
Casos específicos onde o cálculo da diagonal é necessário
O cálculo da diagonal é fundamental em situações onde a precisão dimensional é crucial.
- Instalações elétricas e hidráulicas: Em projetos de instalações elétricas e hidráulicas, o cálculo da diagonal pode auxiliar no posicionamento correto de dutos e cabos, otimizando o espaço e a funcionalidade do sistema.
- Design de peças e produtos: Em projetos de design industrial, o cálculo da diagonal é usado para determinar as medidas e a forma de peças e produtos, como móveis, utensílios e equipamentos.
Caso de estudo: Instalação de uma escada
Uma empresa de construção civil precisa instalar uma escada em um espaço retangular de 3 metros de largura e 4 metros de comprimento. Qual o comprimento mínimo da escada necessária?Aplicando o Teorema de Pitágoras:
d² = 3² + 4² = 9 + 16 = 25
d = √25 = 5 metros
A escada precisa ter, no mínimo, 5 metros de comprimento para alcançar o ponto oposto do espaço retangular.
Simplificação de cálculos
A simplificação de cálculos é crucial para facilitar a determinação da diagonal de um retângulo sem o auxílio de uma calculadora. Compreender as propriedades matemáticas e os padrões nos cálculos permite obter resultados de forma mais eficiente e precisa. Esta seção explorará técnicas para simplificar expressões matemáticas, fornecendo exemplos práticos e uma tabela comparativa para ilustrar as diferentes simplificações.Compreender as técnicas de simplificação permite resolver problemas de forma mais rápida e precisa, especialmente em situações onde o uso de calculadora não é possível.
A aplicação dessas técnicas otimiza o processo de cálculo, tornando-o mais acessível e prático.
Identificação de Padrões
Os cálculos envolvendo o Teorema de Pitágoras, fundamental para determinar a diagonal, podem ser simplificados reconhecendo padrões nos valores. Observar as relações entre os lados do retângulo, especialmente quando são múltiplos de um mesmo número, permite simplificar as etapas de cálculo. Por exemplo, se os lados de um retângulo forem 3 e 6, ambos múltiplos de 3, podemos simplificar a expressão matemática antes de calcular a raiz quadrada.
Técnicas de Simplificação de Expressões
Diversas técnicas podem ser aplicadas para simplificar expressões matemáticas envolvidas no cálculo da diagonal. A fatoração é uma técnica útil quando os números envolvidos possuem fatores comuns. Por exemplo, se os lados do retângulo forem 5 e 10, podemos fatorar o 10 como 2 x 5. Essa simplificação pode reduzir a complexidade da expressão final. Outro recurso importante é a busca por termos semelhantes, que podem ser combinados para obter uma forma mais concisa da expressão.
Exemplos de Simplificação de Equações
Para ilustrar a simplificação de equações, considere o seguinte exemplo: calcular a diagonal de um retângulo com lados medindo 8 cm e 12 cm.
d² = 8² + 12²d² = 64 + 144d² = 208d = √208
Ao notar que 208 é divisível por 4, podemos simplificar a expressão.
d = √(4 x 52)d = √4 x √52d = 2√52
Observe que √52 também pode ser simplificada. Continuando o processo, temos:
d = 2√(4 x 13)d = 2 x 2√13d = 4√13
Este exemplo demonstra como a fatoração pode simplificar o cálculo da diagonal.
Tabela de Simplificações
A tabela a seguir apresenta diferentes casos de lados de um retângulo e suas respectivas simplificações:
| Lado 1 (a) | Lado 2 (b) | Diagonal (d) |
|---|---|---|
| 3 | 4 | 5 |
| 6 | 8 | 10 |
| 5 | 12 | √169 = 13 |
| 8 | 15 | √289 = 17 |
| 9 | 12 | √225 = 15 |
Propriedades Matemáticas
As propriedades matemáticas, como a fatoração e as propriedades das raízes quadradas, são fundamentais para a simplificação dos cálculos. A fatoração permite decompor um número em seus fatores primos, facilitando a simplificação de expressões matemáticas. A compreensão das propriedades das raízes quadradas permite transformar a expressão √(a x b) em √a x √b, possibilitando a simplificação.
Erros comuns e como evitá-los
Ao calcular a diagonal de um retângulo utilizando o Teorema de Pitágoras, é fundamental estar atento a possíveis erros. A compreensão dos potenciais deslizes e a adoção de boas práticas são cruciais para garantir precisão nos cálculos. Este tópico detalha os erros comuns e apresenta estratégias para evitá-los, desde a correta aplicação do teorema até a utilização de unidades de medida apropriadas.A aplicação incorreta do Teorema de Pitágoras, bem como a falta de atenção aos detalhes, pode levar a resultados imprecisos.
A escolha de métodos de cálculo inadequados também pode contribuir para erros, destacando a importância de entender as limitações e vantagens de cada estratégia.
Identificação de Erros na Aplicação do Teorema de Pitágoras
O Teorema de Pitágoras estabelece uma relação fundamental entre os lados de um triângulo retângulo. Para calcular a diagonal de um retângulo, é necessário identificar os lados adjacentes ao ângulo reto como catetos do triângulo retângulo imaginário formado pela diagonal e os lados do retângulo. Um erro comum é a confusão na identificação dos catetos, levando a cálculos incorretos.
Causas de Erros e Correções
Um dos erros mais comuns é a substituição incorreta dos valores nos termos do Teorema de Pitágoras. Por exemplo, ao invés de elevar ao quadrado os comprimentos dos lados, alguns utilizam a adição direta, ou a multiplicação, resultando em um resultado errôneo. Para corrigir isso, é crucial entender e aplicar corretamente a fórmula:
a² + b² = c²
, onde ‘a’ e ‘b’ são os comprimentos dos lados do retângulo e ‘c’ é o comprimento da diagonal.Outro erro comum é o uso de unidades de medida inconsistentes. Por exemplo, calcular um lado em centímetros e outro em metros, sem realizar a conversão prévia. Para evitar esse erro, certifique-se de que todas as medidas estejam na mesma unidade.
Prevenção de Erros de Arredondamento
Arredondamentos intermediários podem levar a erros cumulativos. Evitar arredondamentos desnecessários em etapas intermediárias é crucial para minimizar esses erros. Se necessário, utilize um número maior de casas decimais nos cálculos intermediários e apenas arredonde o resultado final.
Uso de Unidades de Medida Adequadas
O uso de unidades de medida adequadas é essencial para a precisão dos cálculos. Utilizar centímetros para um lado e metros para outro, sem realizar a conversão, resultará em um cálculo incorreto. Por exemplo, se os lados de um retângulo medem 3 metros e 4 metros, a diagonal será calculada em metros.
Comparação de Métodos de Cálculo
Existem diferentes métodos para calcular a diagonal de um retângulo. A comparação dos métodos pode ajudar a identificar possíveis erros e escolher o método mais apropriado. No entanto, o método mais direto e preciso para a maioria dos casos é o Teorema de Pitágoras. Outros métodos, como aproximações ou fórmulas alternativas, podem apresentar erros de arredondamento ou limitações em situações específicas.
Dicas e truques para cálculos rápidos
Para calcular a diagonal de um retângulo sem calculadora de forma eficiente, é fundamental dominar técnicas que otimizem os cálculos mentais. Essas dicas irão auxiliar na simplificação de operações e na identificação de padrões, permitindo resultados mais rápidos e precisos.
Comparação de Métodos
Existem diferentes métodos para determinar a diagonal de um retângulo. O Teorema de Pitágoras é o mais comum e geralmente o mais versátil. Entretanto, dependendo dos valores dos lados do retângulo, outros métodos podem se mostrar mais eficientes. A escolha do método ideal dependerá dos números envolvidos.
Dicas para Cálculos Facilitados
Compreender as propriedades dos números e suas relações é crucial para simplificar cálculos. Identificar padrões e relações matemáticas pode reduzir significativamente o tempo gasto em cálculos mentais.
Reconhecimento de Padrões
O reconhecimento de padrões em números facilita a execução de cálculos mentais mais rapidamente. Por exemplo, quadrados perfeitos (1, 4, 9, 16, 25, 36, 49, 64, 81, 100…) e seus múltiplos são frequentemente encontrados em problemas de geometria. Saber de cor as tabuadas e os primeiros quadrados perfeitos permite que você realize cálculos complexos de forma mais eficiente.
Exemplos Práticos
Considere um retângulo com lados medindo 3 cm e 4 cm. Aplicando o Teorema de Pitágoras, a diagonal (d) é calculada como d² = 3² + 4² = 9 + 16 = 25, então d = √25 = 5 cm. Note que 3, 4 e 5 formam uma terna pitagórica, facilitando o cálculo. Em outro exemplo, um retângulo com lados 6 cm e 8 cm, a diagonal seria √(6² + 8²) = √(36 + 64) = √100 = 10 cm.
Neste caso, os números são múltiplos de 2, facilitando o cálculo mental.
Lista de Dicas para Cálculos Rápidos
- Memorizar as tabuadas e os primeiros quadrados perfeitos é fundamental para cálculos rápidos.
- Identificar e aproveitar ternas pitagóricas simplifica significativamente os cálculos.
- Decompor números em fatores primos pode auxiliar em simplificações.
- Reconhecer padrões em sequências numéricas pode acelerar os cálculos.
- Utilizar a propriedade distributiva em cálculos de multiplicação pode agilizar o processo.
- Estimar resultados antes de calcular pode ajudar a verificar a plausibilidade dos resultados.
Reforço e revisão do conteúdo
Para consolidar o aprendizado sobre o cálculo da diagonal de um retângulo sem o uso de calculadora, esta seção apresenta um resumo dos conceitos-chave, exercícios de revisão e um glossário para facilitar a compreensão e a aplicação prática. Compreender as técnicas apresentadas permitirá resolver problemas de geometria de forma eficiente e eficaz, mesmo sem recursos tecnológicos.
Tabela de Resumo dos Conceitos
A tabela a seguir resume os principais conceitos abordados, facilitando a revisão e a compreensão dos passos para calcular a diagonal de um retângulo sem o auxílio de calculadora.
| Conceito | Descrição |
|---|---|
| Teorema de Pitágoras | Um teorema fundamental da geometria que estabelece a relação entre os lados de um triângulo retângulo. |
| Diagonal de um Retângulo | A linha que conecta dois vértices opostos de um retângulo. |
| Cálculo sem Calculadora | Métodos para determinar a diagonal utilizando operações aritméticas básicas, como adição, subtração, multiplicação e extração de raízes quadradas. |
| Simplificação de Cálculos | Técnicas para tornar os cálculos mais fáceis e rápidos, como fatoração e uso de propriedades matemáticas. |
Questões de Revisão
As questões a seguir visam avaliar a compreensão dos conceitos apresentados.
- Qual a fórmula para calcular a diagonal de um retângulo utilizando o Teorema de Pitágoras?
- Explique como simplificar os cálculos para determinar a diagonal de um retângulo sem utilizar uma calculadora.
- Descreva um exemplo prático onde o cálculo da diagonal de um retângulo seja relevante.
- Liste os erros mais comuns ao calcular a diagonal de um retângulo sem calculadora e como evitá-los.
Glossário de Termos
Este glossário apresenta os termos mais importantes abordados, com suas respectivas definições.
- Teorema de Pitágoras: Um teorema fundamental da geometria euclidiana que estabelece a relação entre os lados de um triângulo retângulo. A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
- Retângulo: Um quadrilátero com quatro ângulos retos e lados opostos congruentes.
- Diagonal: A linha que conecta dois vértices opostos de uma figura geométrica.
- Catetos: Os dois lados de um triângulo retângulo que formam o ângulo reto.
- Hipotenusa: O lado oposto ao ângulo reto em um triângulo retângulo.
Exercícios Práticos
Para fixar o conteúdo, seguem alguns exercícios práticos.
- Um retângulo possui lados medindo 3 cm e 4 cm. Calcule o comprimento da diagonal sem utilizar uma calculadora.
- Um terreno retangular possui 12 metros de largura e 16 metros de comprimento. Qual o comprimento da diagonal do terreno? Apresente os cálculos.
- Um construtor precisa calcular a diagonal de uma placa retangular de 5 m de largura por 12 m de comprimento. Como ele pode fazer isso sem calculadora?
Revisão Completa
A revisão completa compreende o entendimento do Teorema de Pitágoras aplicado ao cálculo da diagonal de um retângulo, a simplificação de cálculos para otimizar o processo e a aplicação prática em situações reais, com exemplos detalhados. O conhecimento da relação entre os lados e a diagonal permite a resolução de problemas geométricos sem a necessidade de recursos tecnológicos.
Concluindo, aprendemos métodos para calcular a diagonal de um retângulo sem calculadora, desde a aplicação do Teorema de Pitágoras até técnicas alternativas. Os exemplos práticos e as simplificações apresentadas facilitarão a compreensão e a aplicação desses conceitos em diferentes contextos. A ênfase na precisão e nos cálculos manuais permite um aprendizado mais profundo e prático, aprimorando as habilidades de resolução de problemas em geometria.
Qual a fórmula básica para calcular a diagonal de um retângulo usando o Teorema de Pitágoras?
A fórmula é d² = a² + b², onde ‘d’ representa a diagonal e ‘a’ e ‘b’ são os lados do retângulo.
Como simplificar os cálculos quando os lados do retângulo são números quadrados perfeitos?
Quando os lados são quadrados perfeitos, a extração da raiz quadrada da soma dos quadrados é simplificada.
Quais são os possíveis erros ao aplicar o Teorema de Pitágoras?
Erros comuns incluem confusão na aplicação da fórmula, erros de cálculo e a falta de atenção às unidades de medida.
Como arredondar os resultados para valores racionais?
O arredondamento deve ser feito com base na precisão requerida pela aplicação e seguindo as regras matemáticas apropriadas.












