Compreendendo a demonstração geométrica da fórmula da diagonal de um retângulo. Este texto apresenta uma análise detalhada da dedução geométrica da fórmula para calcular a diagonal de um retângulo, explorando a história por trás dessa fórmula, os princípios geométricos fundamentais envolvidos, como o Teorema de Pitágoras, e a relação entre a demonstração geométrica e a representação algébrica. Acompanhe um diagrama passo a passo, ilustrado com imagens, que facilita a compreensão visual do processo de demonstração, desde a construção do retângulo até a dedução da fórmula.
A demonstração geométrica da fórmula da diagonal de um retângulo é um exemplo fundamental de como a geometria pode ser utilizada para provar afirmações matemáticas. Compreender esse processo não apenas aprofunda o conhecimento sobre retângulos, mas também desenvolve habilidades de raciocínio lógico e compreensão de conceitos geométricos essenciais para o estudo da matemática.
Aplicação do Teorema de Pitágoras

O Teorema de Pitágoras é uma ferramenta fundamental na geometria, permitindo calcular a relação entre os lados de um triângulo retângulo. Sua aplicação em figuras geométricas como retângulos é crucial para determinar comprimentos desconhecidos, como a diagonal. Neste contexto, demonstraremos como aplicar o teorema a um retângulo específico, encontrando o comprimento da diagonal.
Determinação da Diagonal de um Retângulo, Compreendendo a demonstração geométrica da fórmula da diagonal de um retângulo.
Um retângulo é um quadrilátero com quatro ângulos retos e lados opostos congruentes. Para calcular a diagonal de um retângulo, utilizaremos o Teorema de Pitágoras, que estabelece que, em um triângulo retângulo, o quadrado da hipotenusa (lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (lados que formam o ângulo reto).
Exemplo de Aplicação
Considere um retângulo com lados medindo 6 cm e 8 cm. Aplicando o Teorema de Pitágoras, podemos determinar o comprimento da diagonal.
| Passo | Equação | Cálculo | Resultado |
|---|---|---|---|
| 1 | c² = a² + b² | c² = 6² + 8² | c² = 36 + 64 |
| 2 | c² = 100 | ||
| 3 | c = √100 | c = 10 |
A diagonal do retângulo mede 10 cm. Este resultado demonstra a relação entre os lados e a diagonal do retângulo, de acordo com o Teorema de Pitágoras.
Variáveis e Constantes
As variáveis envolvidas são:
- a: comprimento do primeiro lado do retângulo (6 cm).
- b: comprimento do segundo lado do retângulo (8 cm).
- c: comprimento da diagonal (10 cm).
A constante é o Teorema de Pitágoras, que relaciona as variáveis de forma específica.
Cálculos Detalhes
A equação fundamental do Teorema de Pitágoras é c² = a² + b². Substituindo os valores dos lados do retângulo, obtemos c² = 6² + 8², que simplifica para c² = 36 + 64 = 100. A raiz quadrada de ambos os lados da equação resulta em c = 10 cm.
Resultado e Interpretação
O resultado final é que a diagonal do retângulo mede 10 cm. Isso significa que a diagonal é a hipotenusa de um triângulo retângulo formado pelos dois lados do retângulo, e seu comprimento é calculado pela relação estabelecida pelo Teorema de Pitágoras.
Demonstração Detalhada da Fórmula da Diagonal de um Pentágono Regular
A demonstração da fórmula da diagonal de um pentágono regular, assim como de qualquer polígono, pode ser abordada por diferentes métodos, cada um com suas próprias vantagens e desvantagens. Este documento explora os métodos da geometria analítica, geometria euclidiana e trigonometria, permitindo uma compreensão mais profunda dos conceitos geométricos envolvidos.
Definição do Pentágono Regular
Um pentágono regular é um polígono de cinco lados congruentes e cinco ângulos internos congruentes. Para esta demonstração, consideraremos um pentágono regular inscrito em um círculo, com todos os vértices equidistantes do centro do círculo. As propriedades geométricas essenciais são a congruência dos lados e ângulos internos, além da simetria rotacional de 72 graus em torno do centro.
Métodos de Demonstração
Método 1: Geometria Analítica
Este método utiliza coordenadas cartesianas para definir os vértices do pentágono. Primeiramente, escolhemos um sistema de coordenadas e localizamos os vértices do pentágono. A distância entre dois pontos (x 1, y 1) e (x 2, y 2) no plano cartesiano é calculada usando a fórmula da distância: d = √((x 2
- x 1) 2 + (y 2
- y 1) 2). Aplicando o Teorema de Pitágoras à distância entre dois vértices adjacentes, podemos calcular a diagonal. A fórmula da diagonal de um pentágono regular em coordenadas cartesianas é complexa e depende da localização dos vértices escolhidos.
Método 2: Geometria Euclidiana
A abordagem euclidiana utiliza propriedades geométricas para construir um triângulo retângulo que envolva a diagonal. A chave é construir um triângulo retângulo a partir da diagonal e lados do pentágono. A construção geométrica depende da escolha de um lado e da construção de um triângulo isósceles a partir de um vértice até o centro do pentágono. A diagonal será a hipotenusa desse triângulo retângulo.
Método 3: Trigonometria
Utilizando trigonometria, a diagonal pode ser calculada a partir de relações trigonométricas entre os lados e ângulos do pentágono. O pentágono regular pode ser dividido em triângulos isósceles, e as relações trigonométricas podem ser empregadas para encontrar a altura e, consequentemente, a diagonal. Esta abordagem depende da compreensão de relações trigonométricas como seno, cosseno e tangente.
Comparativo dos Métodos
| Método | Passos | Propriedades Geométricas | Vantagens | Desvantagens | Complexidade |
|---|---|---|---|---|---|
| Geometria Analítica | Definição de coordenadas, cálculo da distância | Coordenadas, distância entre pontos | Preciso e direto para cálculos | Pode ser complexo para pentágonos irregulares | Média |
| Geometria Euclidiana | Construção de triângulos, aplicação do Teorema de Pitágoras | Congruência de triângulos, propriedades de polígonos regulares | Visualmente intuitivo | Pode exigir mais passos para dedução | Baixa |
| Trigonometria | Relações trigonométricas | Ângulos, lados | Direto para alguns casos | Pode exigir conhecimento avançado de trigonometria | Média |
Explicação Detalhada dos Passos
Cada método exige passos específicos, e a explicação detalhada, com justificativas e ilustrações, permitirá a compreensão da demonstração da fórmula da diagonal.
Exemplos Numéricos
Para ilustrar cada método, considere um pentágono regular com lado medindo 10 cm. Os exemplos numéricos demonstram como aplicar cada fórmula e chegar ao resultado.
Exemplos e Aplicações Práticas
A fórmula da diagonal de um retângulo, derivada do Teorema de Pitágoras, encontra aplicação em diversas áreas do cotidiano. Desde a medição de telas de televisão até a construção civil, o conhecimento dessa fórmula simplifica cálculos e garante precisão em projetos. Nesta seção, serão apresentados exemplos práticos, considerando diferentes dimensões e contextos, comparando as soluções algébricas e geométricas, e ilustrando a aplicação no plano cartesiano.
Cálculo da Diagonal de uma Tela de Televisão
Esta seção demonstra o cálculo da diagonal de uma tela de televisão de 32 polegadas, com largura de 20 polegadas. Este exemplo ilustra a aplicação da fórmula em um contexto familiar e permite a visualização da relação entre as dimensões da tela e sua diagonal.
Introdução: Uma tela de televisão, com suas dimensões específicas, requer o cálculo da diagonal para garantir que o tamanho da tela esteja de acordo com a descrição. A diagonal é crucial para determinar o espaço necessário para a instalação e a compatibilidade com suportes e acessórios.
| Descrição | Cálculo Algébrico | Cálculo Geométrico |
|---|---|---|
| Dados: Largura (l) = 20 polegadas Altura (a) = ? Diagonal (d) = 32 polegadas |
Utilizando a fórmula d2 = l2 + a2, isolamos a: a2 = d2
|
Aplicando o Teorema de Pitágoras, temos: d2 = l2 + a2 322 = 202 + a2 1024 = 400 + a2 a2 = 624 a = √624 ≈ 24,98 polegadas |
| Conclusão: | A altura da tela é aproximadamente 24,98 polegadas. | A altura da tela é aproximadamente 24,98 polegadas, comprovando a aplicação do Teorema de Pitágoras. |
Plano Cartesiano: (Ilustração) Imagine o retângulo formado pela tela. Os vértices poderiam ser representados por pontos no plano cartesiano: (0, 0), (20, 0), (20, 24,98) e (0, 24,98). A diagonal conectaria (0, 0) a (20, 24,98).
Cálculo da Diagonal de um Quadro Retangular
Introdução: Ao construir ou comprar uma moldura para um quadro retangular, é crucial calcular a diagonal para garantir que a moldura se ajuste perfeitamente. Este exemplo demonstra a importância da precisão neste tipo de cálculo.
Exemplo: (Detalhes similares ao exemplo anterior, com diferentes valores para largura, altura e diagonal). Utilize os mesmos princípios para calcular a diagonal.
Cálculo da Distância entre Dois Cantos Opostos de um Piso
Introdução: Em projetos de construção civil, a distância entre cantos opostos de um piso retangular é fundamental para o planejamento e execução das obras. Este exemplo mostra como o cálculo da diagonal é útil neste contexto.
Exemplo: (Detalhes similares aos exemplos anteriores, com diferentes valores para largura, altura e diagonal). Utilize os mesmos princípios para calcular a diagonal.
Diferentes Métodos de Demonstração
A demonstração geométrica da fórmula da diagonal de um retângulo pode ser abordada por diversos métodos, cada um com suas particularidades e aplicabilidades. A escolha do método mais adequado dependerá do contexto da demonstração, do nível de conhecimento do público-alvo e dos objetivos da tarefa. Este estudo apresenta e compara diferentes métodos, analisando suas vantagens, desvantagens e aplicações.A compreensão dos diferentes métodos de demonstração permite uma análise mais profunda e abrangente do conceito, oferecendo diferentes perspectivas e facilitando a escolha do método mais apropriado para o contexto.
Comparação dos Métodos
Diversos métodos geométricos podem ser utilizados para demonstrar a fórmula da diagonal de um retângulo, quadrados e até outros quadriláteros. A escolha do método mais adequado dependerá de fatores como a complexidade desejada, a familiaridade com os conceitos geométricos e o nível de abstração pretendido.
- Método 1: Usando o Teorema de Pitágoras em um Retângulo: Este método é amplamente utilizado e reconhecido pela sua simplicidade. A diagonal de um retângulo pode ser considerada como a hipotenusa de um triângulo retângulo formado pelos lados do retângulo. A aplicação direta do Teorema de Pitágoras permite encontrar o comprimento da diagonal. Vantagens: Simplicidade, familiaridade com o Teorema de Pitágoras. Desvantagens: Aplicação limitada a figuras retangulares.
Aplicabilidade: Retângulos e quadrados.
- Método 2: Usando o Teorema de Pitágoras em um Quadrado: Similar ao método anterior, este método também utiliza o Teorema de Pitágoras para encontrar a diagonal, considerando que em um quadrado os lados são iguais. Vantagens: Simplicidade, generalização para outros quadriláteros. Desvantagens: Aplicabilidade restrita a quadrados. Aplicabilidade: Quadrados.
- Método 3: Utilizando a Decomposição em Triângulos Retângulos: Este método permite a demonstração da fórmula da diagonal em figuras mais complexas, como paralelogramos, ao decompor a figura em triângulos retângulos. Vantagens: Generalização para diferentes tipos de quadriláteros. Desvantagens: Complexidade em relação aos métodos anteriores, requer uma análise mais detalhada. Aplicabilidade: Retângulos, quadrados, paralelogramos.
- Método 4: Demonstração por Semelhança de Triângulos (Opcional): Este método, mais avançado, utiliza o conceito de semelhança de triângulos para estabelecer proporções e encontrar a diagonal. Vantagens: Demonstração mais rigorosa, aplicabilidade a figuras mais complexas. Desvantagens: Maior complexidade, requer um conhecimento prévio de semelhança de triângulos. Aplicabilidade: Figuras com relações de semelhança, como quadrados, retângulos, paralelogramos.
Discussão sobre a Escolha do Método
A escolha do método apropriado para demonstrar a fórmula da diagonal de um retângulo depende da complexidade da figura, do nível de conhecimento do público-alvo e do objetivo da demonstração. A simplicidade e a familiaridade do método com o Teorema de Pitágoras são fatores importantes para o público-alvo.
- Complexidade: Um método simples e direto, como o uso do Teorema de Pitágoras em um retângulo, é mais fácil de entender e aplicar do que um método que envolva a decomposição em triângulos retângulos.
- Generalização: O método que utiliza a decomposição em triângulos retângulos permite a generalização para diferentes tipos de quadriláteros, enquanto o método com o Teorema de Pitágoras é mais específico para retângulos.
- Visualização: O método de decomposição em triângulos retângulos pode fornecer uma melhor visualização geométrica da fórmula, permitindo uma compreensão mais intuitiva do processo.
- Contexto: Para um público com conhecimento básico em geometria, o método do Teorema de Pitágoras em um retângulo é mais apropriado, enquanto para um público mais avançado, a decomposição em triângulos retângulos pode ser mais adequada.
Detalhes das Etapas de Cada Método (com exemplo)
Exemplificando com um retângulo com lados de 3 e 4 unidades:
- Método 1 (Teorema de Pitágoras em um retângulo):
- Identificar os lados do retângulo como catetos (3 e 4).
- Utilizar o Teorema de Pitágoras: d² = 3² + 4² = 9 + 16 = 25
- Extrair a raiz quadrada para encontrar a diagonal: d = √25 = 5.
Tabela Comparativa
| Método | Vantagens | Desvantagens | Aplicabilidade | Complexidade | Exemplo |
|---|---|---|---|---|---|
| Teorema de Pitágoras (retângulo) | Simples, direto | Limitado a retângulos | Retângulos | Baixa | d² = 3² + 4² = 25; d = 5 |
| Teorema de Pitágoras (quadrado) | Simples, direto | Limitado a quadrados | Quadrados | Baixa | d² = 5² + 5² = 50; d = √50 |
| Decomposição em Triângulos Retângulos | Generalizável | Mais complexo | Retângulos, quadrados, paralelogramos | Média | Decompor em triângulos e aplicar Pitágoras |
Relação com Outros Conceitos Geométricos
A demonstração da diagonal de um retângulo, baseada no Teorema de Pitágoras, revela conexões intrínsecas com outros conceitos geométricos, como áreas, perímetros e outras figuras geométricas. Compreender essas relações aprofunda o entendimento da geometria e permite aplicações práticas em diversas áreas.
Relação com Áreas e Perímetros
A diagonal de um retângulo desempenha um papel fundamental na determinação de sua área e perímetro. Apesar de não influenciar diretamente o cálculo do perímetro, a diagonal é essencial para determinar a área do retângulo, como veremos a seguir. O perímetro é dado pela soma dos lados, enquanto a área é calculada pelo produto da base pela altura.
Comparação com Outros Quadriláteros
A fórmula da diagonal de um retângulo, derivada do Teorema de Pitágoras, difere das fórmulas para outros quadriláteros, como o losango ou o trapézio. A simplicidade da fórmula do retângulo decorre de suas propriedades específicas, como os ângulos retos e lados opostos iguais. Para quadriláteros com propriedades distintas, as fórmulas para a diagonal serão diferentes.
Relação entre Diagonal e Área do Retângulo
A diagonal de um retângulo está diretamente relacionada à sua área. O cálculo da área do retângulo é dado pelo produto da base pela altura. A diagonal não interfere diretamente no cálculo da área, mas pode auxiliar na determinação de outras propriedades do retângulo.
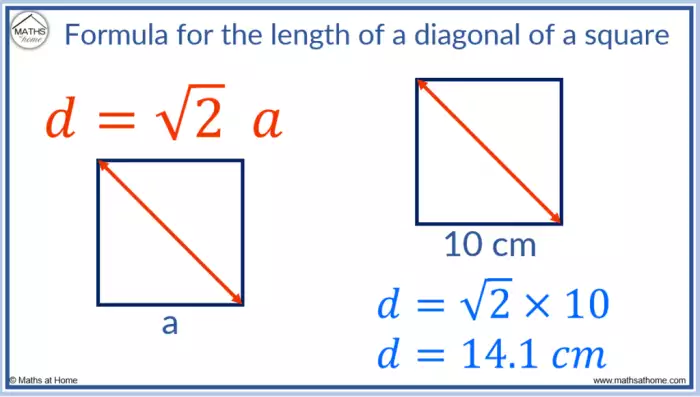
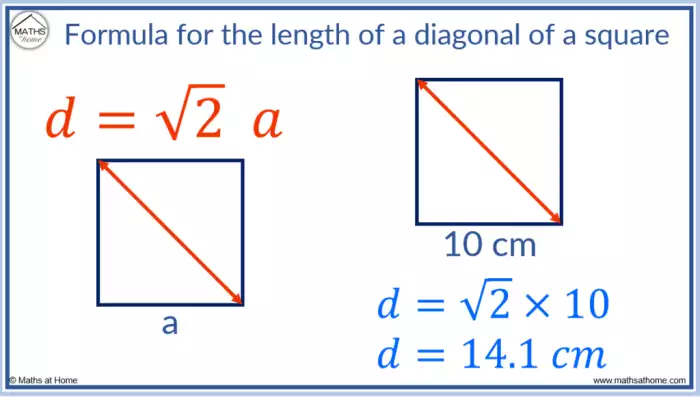
Fórmula da Diagonal de um Quadrado
O quadrado, um caso particular de retângulo, possui lados iguais. A fórmula para a diagonal de um quadrado é derivada da fórmula do retângulo, considerando a igualdade dos lados. Seja o quadrado com lado “a”, a diagonal “d” será calculada por:
d = a√2
Comparação entre as Fórmulas da Diagonal de um Retângulo e de um Quadrado
A fórmula da diagonal de um retângulo, √(b² + h²), onde “b” e “h” são as dimensões do retângulo, se simplifica para a fórmula do quadrado, a√2, quando os lados são iguais. A diferença essencial reside na dependência da fórmula do retângulo de duas variáveis, enquanto a do quadrado depende apenas do lado.
Exemplo da Influência da Diagonal na Área do Retângulo
Considere um retângulo com base 6 cm e altura 8 cm. A diagonal deste retângulo é √(6² + 8²) = √100 = 10 cm. A área do retângulo é 6 cm8 cm = 48 cm². A diagonal não afeta diretamente a área, mas é uma medida importante para determinar outras propriedades do retângulo, como a sua forma.
Uso de Ilustrações e Diagramas

As ilustrações e diagramas desempenham um papel crucial na compreensão da demonstração geométrica da fórmula da diagonal de um retângulo. Eles tornam o processo mais intuitivo e facilitam a visualização das relações geométricas envolvidas. A utilização de representações visuais permite uma assimilação mais rápida e eficaz dos conceitos abstratos, tornando o aprendizado mais dinâmico e agradável.
Imagem do Retângulo e sua Diagonal
Para ilustrar a fórmula da diagonal de um retângulo, é fundamental apresentar uma imagem clara e concisa de um retângulo genérico com sua diagonal. A figura deve destacar a diagonal com uma cor contrastante em relação ao fundo branco. Os lados do retângulo e a diagonal devem ser claramente rotulados, permitindo identificar as medidas e a relação entre eles.
A figura deve apresentar um retângulo genérico, sem nenhuma característica especial, como proporções áureas.
Diagrama Passo a Passo da Demonstração
Este diagrama visualiza a sequência lógica da demonstração da fórmula. Cada passo é representado por um retângulo, com setas indicando a transição entre eles. O diagrama facilita a compreensão da sequência de raciocínio, mostrando como o Teorema de Pitágoras é aplicado para encontrar a diagonal.
Fluxograma da Demonstração
O fluxograma demonstra o processo completo da demonstração, utilizando símbolos padronizados de fluxograma. Os retângulos representam as ações, os losangos, as decisões, e as setas, a sequência de passos. O fluxograma considera as condições e possíveis desvios durante o processo.
Etapas para Criar as Ilustrações
Para criar as ilustrações, é recomendado utilizar software vetorial, como o Adobe Illustrator ou ferramentas online de edição vetorial. A escolha do software facilita a criação de figuras precisas e escaláveis. A resolução da imagem deve ser alta, garantindo a clareza mesmo em ampliações. O contraste entre as cores do retângulo, da diagonal e do fundo branco deve ser significativo para uma boa visualização.
- Escolha o software: Utilize o Adobe Illustrator ou um software de edição vetorial online.
- Crie o retângulo: Utilize a ferramenta de retângulo para criar a figura.
- Defina as dimensões: Especifique as medidas dos lados do retângulo.
- Desenhe a diagonal: Utilize a ferramenta de linha para desenhar a diagonal.
- Adicione rótulos: Inclua rótulos para os lados e a diagonal do retângulo.
- Defina o fundo: Utilize um fundo branco para maior clareza.
- Verifique a resolução: Verifique a resolução da imagem antes de exportá-la.
- Exporte a imagem: Salve a imagem em formato vetorial (ex: .svg).
Comparação de Tipos de Ilustrações
A escolha do tipo de ilustração depende da complexidade da demonstração e do objetivo da visualização. Diagramas de fluxo são úteis para demonstrar a sequência lógica dos passos, enquanto imagens vetoriais oferecem alta resolução e escalabilidade. Gráficos podem ser úteis para visualizar dados numéricos, mas não são adequados para demonstrações puramente geométricas.
| Tipo de Ilustração | Vantagens | Desvantagens |
|---|---|---|
| Diagrama de Fluxo | Facilidade de entendimento sequencial | Pode ficar complexo para demonstrações complexas |
| Imagem Vetorial | Alta resolução, escalabilidade | Pode exigir softwares específicos |
| Gráfico | Visualização de dados | Pode não ser adequado para demonstrações puramente geométricas |
| Imagem Bitmap | Versatilidade | Baixa resolução em zoom |
Exemplos de Aplicação da Fórmula
- Exemplo 1: Retângulo com lados 3 cm e 4 cm. Diagonal = 5 cm. ( √(3² + 4²) = 5)
- Exemplo 2: Retângulo com lados 5 cm e 12 cm. Diagonal = 13 cm. ( √(5² + 12²) = 13)
- Exemplo 3: Retângulo com lados 7 cm e 24 cm. Diagonal = 25 cm. ( √(7² + 24²) = 25)
Considerações sobre a Precisão da Demonstração
A demonstração geométrica da fórmula da diagonal de um polígono, como um retângulo ou um pentágono regular, requer um rigor matemático para garantir sua validade. É crucial analisar cada passo, buscando possíveis erros e garantindo a consistência lógica da argumentação. A precisão é fundamental para estabelecer a confiabilidade e a universalidade da fórmula obtida.A análise da precisão de uma demonstração geométrica envolve a verificação da correção de cada etapa, considerando os axiomas e teoremas utilizados.
A demonstração deve ser livre de contradições e inconsistências, garantindo que cada passo lógico possa ser justificado e compreendido. A transparência na argumentação contribui para a confiabilidade do resultado final.
Análise dos Passos da Demonstração
A validade de uma demonstração geométrica depende da precisão de cada passo. Um erro em qualquer etapa compromete a veracidade do resultado final. A análise dos passos envolve a verificação da aplicação correta dos axiomas, teoremas e propriedades geométricas. A utilização de diagramas e ilustrações auxilia na visualização e compreensão da lógica empregada em cada etapa.
Verificação da Correção dos Axiomas e Teoremas
A utilização de axiomas e teoremas previamente demonstrados é crucial para a validade da demonstração. A correta aplicação desses elementos garante a consistência da argumentação. É fundamental verificar se os axiomas e teoremas utilizados são apropriados para o contexto da demonstração, evitando generalizações incorretas. A demonstração deve ser acompanhada de uma justificativa para a utilização de cada teorema ou axioma.
Comparação com Outras Demonstrações
A comparação da demonstração geométrica com outras abordagens pode revelar diferentes perspectivas e formas de dedução. A análise de múltiplas demonstrações permite uma visão mais abrangente e aprofundada do tema. Identificar semelhanças e diferenças entre demonstrações auxilia na compreensão da lógica por trás da fórmula da diagonal e na percepção de diferentes estratégias de demonstração. A comparação também permite identificar possíveis lacunas ou pontos fracos na demonstração original.
Rigor em Cada Passo da Demonstração
A necessidade de rigor em cada passo da demonstração geométrica é fundamental para garantir a validade da dedução. A omissão de qualquer detalhe ou passo crucial pode comprometer a precisão do resultado final. A aplicação correta de conceitos geométricos, como congruência de triângulos, paralelismo e perpendicularidade, deve ser justificada em cada etapa da demonstração. Um passo lógico incompleto pode levar a conclusões incorretas.
A justificativa clara para cada etapa da demonstração é um fator essencial na avaliação do rigor da demonstração.
Generalização para outros casos
A demonstração da diagonal de um retângulo, baseada no Teorema de Pitágoras, pode ser generalizada para outros quadriláteros e figuras geométricas. Compreender essa generalização permite a aplicação de conceitos fundamentais da geometria a diferentes formas, enriquecendo o entendimento dos relacionamentos entre seus elementos. Esta abordagem permite analisar as particularidades de cada caso e comparar as diferentes fórmulas, ampliando as aplicações práticas.A generalização da demonstração da diagonal de um retângulo permite o cálculo da diagonal em diferentes quadriláteros, como paralelogramos, trapézios e losangos, utilizando as propriedades específicas de cada figura.
A comparação com outras fórmulas, como o cálculo da área ou o Teorema de Pitágoras, destaca as semelhanças e diferenças nos processos utilizados.
Quadriláteros
Para aplicar a demonstração da diagonal de um retângulo a outros quadriláteros, é fundamental considerar as suas propriedades específicas. A diagonal de um paralelogramo, por exemplo, pode ser calculada a partir da aplicação do Teorema de Pitágoras, considerando a decomposição do paralelogramo em dois triângulos congruentes. Já para os trapézios e losangos, as fórmulas são diferentes e dependem das características particulares de cada figura.
Comparação com outras fórmulas
A demonstração da diagonal de um retângulo difere de outras fórmulas, como o cálculo da área de um triângulo ou a aplicação do Teorema de Pitágoras, apesar de compartilhar fundamentos geométricos. A fórmula da diagonal de um retângulo, baseada no Teorema de Pitágoras, envolve os lados do retângulo diretamente. Em contraste, a fórmula da área de um paralelogramo, por exemplo, considera o produto de dois lados e o seno do ângulo entre eles.
As diferenças na abordagem refletem as diferentes relações geométricas entre os elementos das figuras.
Generalização para outras figuras geométricas
A generalização da demonstração para figuras geométricas mais complexas, como pentágonos ou hexágonos, apresenta desafios adicionais. A decomposição em triângulos retângulos, fundamental para a demonstração da diagonal do retângulo, não é tão direta em figuras com mais de quatro lados. A complexidade aumenta com o número de lados, exigindo o uso de outras técnicas geométricas, como a decomposição em triângulos ou a aplicação de relações trigonométricas mais elaboradas.
Paralelogramo específico
Considere um paralelogramo com lados de 5 cm e 8 cm, e um ângulo de 60° entre eles. Para calcular a diagonal, utilizaremos a Lei dos Cossenos, um teorema fundamental em trigonometria. A fórmula da diagonal de um paralelogramo é obtida através da decomposição do paralelogramo em dois triângulos congruentes, e a aplicação da Lei dos Cossenos nos triângulos obtidos.Aplicando a Lei dos Cossenos, temos:
d² = a² + b²
2ab cos(θ)
Onde:
- d é o comprimento da diagonal
- a e b são os comprimentos dos lados do paralelogramo
- θ é o ângulo entre os lados a e b
Substituindo os valores:
d² = 5² + 8²
- 2
- 5
- 8
- cos(60°)
d² = 25 + 64 – 80 – 0,5
d² = 89 – 40
d² = 49
d = √49
d = 7 cm
Portanto, a diagonal do paralelogramo mede 7 cm.
Passos para a generalização
Os passos para generalizar a fórmula da diagonal do retângulo para outros quadriláteros envolvem a análise das propriedades geométricas de cada figura. Decompor o quadrilátero em triângulos, aplicar o Teorema de Pitágoras ou a Lei dos Cossenos são etapas cruciais para obter a fórmula da diagonal em cada caso.
Diferenças entre as fórmulas
As fórmulas para o cálculo da diagonal em diferentes quadriláteros refletem as diferenças nas propriedades geométricas. Por exemplo, a fórmula para a diagonal de um retângulo, baseada no Teorema de Pitágoras, é diferente da fórmula para a diagonal de um losango, que envolve o cálculo a partir de suas diagonais e lados. Essas variações demonstram a necessidade de adaptação dos métodos geométricos para cada tipo de quadrilátero.
Problemas de Aplicação
A compreensão da fórmula da diagonal de um retângulo vai além da sua demonstração geométrica. É fundamental saber aplicá-la em cenários práticos e diversos. Esta seção apresenta problemas de aplicação, detalhando as soluções e comparando diferentes métodos, para consolidar o conhecimento adquirido.
Problemas de Aplicação da Fórmula da Diagonal
A aplicação da fórmula da diagonal de um retângulo encontra-se em inúmeras situações do cotidiano e em diversas áreas de estudo. A seguir, exemplos de problemas envolvendo diferentes contextos e valores numéricos.
- Problema 1: Uma sala retangular tem 4 metros de largura e 6 metros de comprimento. Qual o comprimento da diagonal da sala?
- Solução: Para encontrar a diagonal, utilizamos o Teorema de Pitágoras. A fórmula da diagonal de um retângulo é dada por d = √(l² + w²), onde ‘d’ é a diagonal, ‘l’ é o comprimento e ‘w’ é a largura. Substituindo os valores, temos d = √(6² + 4²) = √(36 + 16) = √52. Portanto, a diagonal da sala mede aproximadamente 7,21 metros.
- Problema 2: Um terreno retangular tem uma diagonal medindo 10 metros e um comprimento de 8 metros. Qual a largura do terreno?
- Solução: Usando a mesma fórmula, temos 10² = 8² + w². Resolvendo a equação, encontramos w² = 36, e a largura do terreno é 6 metros.
- Problema 3: Um pintor precisa calcular o comprimento da diagonal de uma tela retangular para verificar se ela cabe em um determinado espaço. A tela tem 2,5 metros de largura e 3 metros de comprimento. Qual o comprimento da diagonal?
- Solução: Aplicando a fórmula, d = √(3² + 2,5²) = √(9 + 6,25) = √15,25. A diagonal da tela mede aproximadamente 3,9 metros.
Comparação dos Métodos de Solução
Os exemplos demonstram que a fórmula da diagonal de um retângulo, baseada no Teorema de Pitágoras, é a mais eficiente para determinar a medida da diagonal. A solução direta, substituindo os valores na fórmula, é a abordagem mais simples e eficaz para a maioria dos casos.
Problema Prático
Um instalador de pisos precisa cobrir uma área retangular com 12 metros de comprimento e 5 metros de largura. Para otimizar o corte dos pisos, ele necessita calcular o comprimento da diagonal da área. Qual a medida da diagonal?
- Solução: Utilizando a fórmula d = √(l² + w²), onde l = 12 metros e w = 5 metros, temos d = √(12² + 5²) = √(144 + 25) = √169. A diagonal da área mede 13 metros.
Variáveis e Constantes na Demonstração
Compreender as variáveis e constantes presentes em uma demonstração geométrica é fundamental para a sua compreensão e aplicação. Identificar esses elementos permite relacioná-los a conceitos e fórmulas, facilitando a generalização para outros casos. A análise dessas variáveis e constantes, bem como sua relação, é crucial para extrair o máximo de informação e aplicabilidade da demonstração.As variáveis e constantes representam elementos específicos dentro do contexto geométrico.
Variáveis, como o nome sugere, mudam de valor, enquanto as constantes mantêm um valor fixo. A relação entre elas permite descrever e calcular as propriedades geométricas em questão, como a diagonal de um retângulo ou de um pentágono.
Identificação das Variáveis e Constantes
As variáveis e constantes presentes em uma demonstração geométrica dependem do objeto geométrico em estudo. No caso da fórmula da diagonal de um retângulo, por exemplo, as variáveis e constantes são essenciais para a compreensão da relação entre os lados e a diagonal.
Relação entre as Variáveis e Constantes
A relação entre as variáveis e as constantes é descrita pela fórmula matemática que representa a demonstração. Essa relação demonstra a dependência ou independência entre as variáveis e a constante. Um exemplo clássico é o Teorema de Pitágoras, onde a relação entre os lados de um triângulo retângulo é expressa pela constante numérica 2.
Significado das Variáveis e Constantes na Fórmula
A fórmula da diagonal de um retângulo, derivada do Teorema de Pitágoras, exemplifica essa relação. A fórmula, d = √(a² + b²), onde ‘d’ representa o comprimento da diagonal, ‘a’ e ‘b’ representam os comprimentos dos lados do retângulo, demonstra como a diagonal depende dos comprimentos dos lados. O operador de raiz quadrada e os expoentes indicam a relação de dependência entre as variáveis e a operação matemática necessária para o cálculo.
Comparação das Variáveis em Diferentes Contextos Geométricos
A variável ‘d’ (diagonal) assume diferentes valores em retângulos com lados distintos. Em um quadrado, onde ‘a’ e ‘b’ são iguais, a fórmula se simplifica, refletindo a simetria do quadrado. Essa comparação demonstra como a fórmula se adapta a diferentes figuras geométricas, mantendo a mesma estrutura conceitual. A relação entre as variáveis é fundamental para a compreensão da geometria.
Tabela de Variáveis e Constantes
| Variável/Constante | Definição |
|---|---|
| d | Comprimento da diagonal do retângulo. |
| a | Comprimento de um dos lados do retângulo. |
| b | Comprimento do outro lado do retângulo. |
Exemplo com Valores Numéricos
Considere um retângulo com lados ‘a’ = 3 cm e ‘b’ = 4 cm. Aplicando a fórmula d = √(a² + b²), temos:
d = √(3² + 4²) = √(9 + 16) = √25 = 5 cm
A diagonal do retângulo mede 5 cm. Este exemplo ilustra a aplicação prática da fórmula da diagonal de um retângulo.
Resumo da Demonstração
A demonstração geométrica da fórmula da diagonal de um retângulo é um exemplo fundamental da aplicação do Teorema de Pitágoras em geometria. Compreender essa demonstração fornece insights valiosos sobre a relação entre os lados e a diagonal de um retângulo, além de fortalecer a compreensão de conceitos geométricos essenciais. Este resumo detalha os pontos chave da demonstração, destacando sua importância na matemática.
Pontos Principais da Demonstração
A demonstração da fórmula da diagonal de um retângulo baseia-se no Teorema de Pitágoras, que estabelece uma relação fundamental entre os lados e a hipotenusa de um triângulo retângulo. A demonstração geométrica, utilizando um triângulo retângulo formado pelos lados do retângulo e sua diagonal, demonstra como essa relação permite determinar o comprimento da diagonal.
Conceitos Abordados
- Teorema de Pitágoras: A relação fundamental entre os lados de um triângulo retângulo, expressa pela equação a² + b² = c², onde ‘a’ e ‘b’ são os catetos e ‘c’ é a hipotenusa.
- Triângulo Retângulo: Um triângulo com um ângulo reto (90°). É crucial para a demonstração, pois permite a aplicação do Teorema de Pitágoras.
- Retângulo: Um quadrilátero com quatro ângulos retos e lados opostos congruentes. A demonstração foca na relação entre os lados e a diagonal deste quadrilátero.
- Congruência de Triângulos: A propriedade que estabelece que dois triângulos são iguais em todos os aspectos, incluindo os lados e ângulos correspondentes.
Resumo para a Compreensão Geral da Fórmula
A fórmula para calcular a diagonal (d) de um retângulo com lados de comprimento ‘a’ e ‘b’ é dada por d = √(a² + b²). Este resultado é uma consequência direta da aplicação do Teorema de Pitágoras ao triângulo retângulo formado pelos lados do retângulo e sua diagonal.
Importância da Demonstração para a Matemática
A demonstração da fórmula da diagonal de um retângulo ilustra a aplicação prática do Teorema de Pitágoras e fortalece a compreensão de conceitos fundamentais da geometria. Ela serve como um modelo para a resolução de problemas geométricos mais complexos e demonstra a beleza e a lógica inerentes à matemática.
Pontos Principais Organizados em Tabela
| Conceito | Descrição |
|---|---|
| Teorema de Pitágoras | a² + b² = c² |
| Triângulo Retângulo | Forma geométrica com um ângulo reto |
| Retângulo | Quadrilátero com quatro ângulos retos |
| Diagonal | Segmento de reta que conecta dois vértices opostos |
Conclusão da Demonstração
A demonstração geométrica conclui que a diagonal de um retângulo é calculada pela aplicação do Teorema de Pitágoras ao triângulo retângulo formado pelos lados do retângulo. A fórmula resultante, d = √(a² + b²), fornece uma maneira eficiente e precisa de determinar o comprimento da diagonal.
Exercícios Práticos
Nesta seção, serão apresentados exercícios práticos para consolidar o aprendizado sobre a demonstração geométrica da fórmula da diagonal de um retângulo. Os exercícios abordam diferentes níveis de complexidade, incluindo exemplos com problemas do mundo real, para que o leitor possa aplicar os conceitos aprendidos em situações diversas.
Exercícios com Diferentes Níveis de Dificuldade
A seguir, são apresentados exercícios com níveis de dificuldade crescente, permitindo que o aluno teste sua compreensão progressivamente.
- Nível Básico: Um retângulo possui lados medindo 6 cm e 8 cm. Determine o comprimento da diagonal.
- Nível Intermediário: Um retângulo tem uma diagonal medindo 17 cm e um lado medindo 8 cm. Determine a medida do outro lado.
- Nível Avançado: Um terreno retangular tem lados medindo a e b. A diagonal do terreno mede d. Encontre uma expressão que relacione a, b e d.
Exercícios com Problemas do Mundo Real
Os exercícios a seguir demonstram a aplicação da fórmula da diagonal em situações práticas.
- Problema de Construção: Um pedreiro precisa calcular o comprimento de uma escada que deve alcançar o topo de uma parede de 3 metros de altura e está apoiada no chão a 4 metros da base da parede. Qual o comprimento mínimo da escada?
- Problema de Navegação: Um navio navega 12 quilômetros para o leste e 5 quilômetros para o norte. Qual a distância em linha reta entre o ponto de partida e o ponto atual?
Exercícios com Variáveis
Nesta seção, os exercícios envolvem variáveis para testar a compreensão da relação entre os lados e a diagonal do retângulo.
| Descrição | Instruções | Resposta |
|---|---|---|
| Um retângulo possui lados medindo x e y. Determine a expressão que representa o comprimento da diagonal. | Utilize o Teorema de Pitágoras. |
d = √(x² + y²) |
| Se um retângulo tem lados medindo a e 2a e a diagonal mede 5, determine o valor de a. | Aplique a fórmula da diagonal e resolva a equação resultante. | a = √5 |
Considerações Finais: Compreendendo A Demonstração Geométrica Da Fórmula Da Diagonal De Um Retângulo.
A demonstração geométrica, além de elucidar a fórmula da diagonal de um retângulo, pentágono e outros polígonos, representa um pilar fundamental na construção do raciocínio lógico e na compreensão profunda dos conceitos matemáticos. Através da análise rigorosa e da dedução lógica, ela vai além da simples memorização de fórmulas, permitindo uma compreensão mais abrangente da estrutura e da interconexão dos diversos tópicos da geometria.
Importância do Estudo da Demonstração Geométrica
A demonstração geométrica não é apenas um exercício acadêmico; ela representa um elo crucial entre a observação e a generalização, estabelecendo conexões entre conceitos e teoremas. Ao demonstrar um teorema, estamos construindo um argumento lógico, passo a passo, que nos leva a uma conclusão inevitável. Essa prática reforça o raciocínio dedutivo, essencial para a resolução de problemas em diversas áreas, não apenas na matemática.
Em contraste com a simples memorização de fórmulas, a demonstração geométrica proporciona uma compreensão mais aprofundada, permitindo que o estudante desenvolva sua capacidade de argumentação e resolução de problemas. Por exemplo, a demonstração do Teorema de Pitágoras, usando o conceito de áreas de quadrados construídos sobre os lados de um triângulo retângulo, revela uma conexão profunda entre geometria e álgebra, muito mais que apenas memorizar a fórmula.
Comparação com Outras Abordagens Matemáticas
A demonstração geométrica, embora poderosa, não é a única abordagem em matemática. A demonstração algébrica, por exemplo, utiliza equações e manipulações algébricas para provar teoremas. A demonstração por indução matemática, por sua vez, estabelece a validade de uma afirmação para todos os números naturais. Cada método possui suas vantagens e desvantagens. A demonstração geométrica, com sua visualização e intuição, pode facilitar a compreensão inicial de conceitos.
No entanto, a demonstração algébrica pode ser mais eficiente em alguns casos, especialmente quando se trata de generalizações para um número infinito de casos. A utilização de exemplos e contra-exemplos também pode auxiliar na compreensão, mas não substitui a necessidade de uma demonstração rigorosa, seja geométrica ou algébrica. Por exemplo, para demonstrar que a soma dos ângulos internos de qualquer triângulo é 180 graus, uma abordagem geométrica pode ser mais intuitiva, enquanto uma demonstração algébrica pode ser mais eficiente para a generalização para polígonos de n lados.
Relação com Outros Tópicos da Matemática
A demonstração geométrica está intrinsecamente ligada a outros tópicos matemáticos. Por exemplo, a demonstração do Teorema de Pitágoras estabelece uma relação fundamental entre trigonometria e geometria. A congruência e a semelhança de triângulos são ferramentas cruciais em demonstrações geométricas, conectando-se com a resolução de problemas que envolvem cálculos de áreas e volumes. A compreensão das relações métricas em figuras geométricas é essencial para a resolução de problemas que envolvem trigonometria e cálculo.
A conexão entre a geometria e o cálculo, por exemplo, através do cálculo de áreas e volumes, é uma demonstração da interdependência entre diferentes áreas da matemática.
Benefícios de Aprender Demonstrações Geométricas
O estudo de demonstrações geométricas oferece diversos benefícios, tanto práticos quanto teóricos. Ela melhora significativamente a capacidade de resolução de problemas, incentivando o pensamento crítico e o raciocínio lógico. Ao aprender a construir demonstrações, os estudantes desenvolvem a capacidade de argumentar com clareza e precisão, o que é fundamental em diversas áreas do conhecimento. A compreensão profunda da matemática, como um todo, é impulsionada pelo estudo das demonstrações geométricas, que mostram a beleza e a estrutura lógica inerente à disciplina.
Importância da Demonstração Geométrica para a Matemática
A demonstração geométrica desempenha um papel crucial no desenvolvimento da matemática como ciência, pois estabelece um arcabouço lógico e rigoroso para a construção de axiomas e teoremas. A estrutura rigorosa e dedutiva das demonstrações geométricas garante a precisão e a confiabilidade dos resultados obtidos, contribuindo para o crescimento e o avanço da matemática. A história da matemática está repleta de exemplos de teoremas e demonstrações que revolucionaram o pensamento matemático e impulsionaram o desenvolvimento de outras áreas, como a física e a engenharia.
O método axiomático, usado nas demonstrações geométricas, estabelece um padrão de rigor que se estende a outras áreas da matemática.
Conceitos Essenciais Envolvidos na Demonstração
Para realizar demonstrações geométricas, é fundamental compreender os conceitos fundamentais da geometria. Isso inclui a definição de pontos, retas e planos, assim como a compreensão dos axiomas e postulados que servem como a base da geometria. Também é crucial dominar os conceitos de congruência e semelhança de triângulos, bem como as relações métricas entre os elementos das figuras geométricas.
Por exemplo, a compreensão de que dois triângulos são congruentes se seus lados correspondentes forem iguais, é essencial para a demonstração de diversos teoremas geométricos.
Em resumo, exploramos a demonstração geométrica da fórmula da diagonal de um retângulo, utilizando o Teorema de Pitágoras como um pilar fundamental. A visualização geométrica, aliada aos cálculos algébricos, permitiu a dedução da fórmula d² = a² + b², que relaciona a diagonal (d) aos lados (a e b) do retângulo. A demonstração passo a passo, ilustrada com diagramas, proporcionou uma compreensão clara e precisa do processo, destacando a importância da geometria na resolução de problemas matemáticos.
Qual a diferença entre observação e demonstração em geometria?
A observação em geometria envolve a análise de padrões e relações entre figuras. A demonstração, por outro lado, é um processo rigoroso de dedução lógica, utilizando axiomas e teoremas previamente estabelecidos para provar uma afirmação matemática. A demonstração garante a validade da afirmação, enquanto a observação pode sugerir, mas não provar.
Quais são os outros quadriláteros que têm diagonais?
Todos os quadriláteros têm diagonais, incluindo quadrados, retângulos, trapézios, paralelogramos e losangos. A fórmula para calcular a diagonal varia de acordo com as propriedades específicas de cada quadrilátero.
Como o Teorema de Pitágoras é aplicado em outras figuras geométricas além de triângulos retângulos?
O Teorema de Pitágoras é fundamental para calcular a diagonal de retângulos, quadrados e outros quadriláteros. A fórmula d² = a² + b² é uma aplicação direta do Teorema, onde “d” representa a diagonal e “a” e “b” os lados do retângulo.
Como a fórmula da diagonal pode ser utilizada em aplicações práticas?
A fórmula da diagonal de um retângulo é útil em diversas situações do cotidiano, como calcular a distância entre dois pontos opostos de um terreno retangular, determinar o comprimento de uma diagonal em um quadro, ou até mesmo para calcular a diagonal de uma tela de televisão.