Como encontrar a diagonal de um retângulo com valores decimais para comprimento e largura? Este guia completo explora o cálculo da diagonal de um retângulo, desde a definição fundamental até exemplos práticos com valores decimais. Compreender essa relação geométrica é crucial para diversos campos, como engenharia, arquitetura e até mesmo para solucionar problemas do dia a dia.
O cálculo da diagonal de um retângulo, mesmo com valores decimais, segue um princípio fundamental: o Teorema de Pitágoras. Este artigo apresenta a fórmula matemática, demonstra sua aplicação com exemplos detalhados e explica os passos para chegar ao resultado correto, garantindo precisão em cada etapa. Além disso, exploraremos métodos alternativos e considerações geométricas para uma compreensão mais profunda.
Introdução ao Cálculo da Diagonal de um Retângulo
A diagonal de um retângulo é o segmento de reta que une dois vértices opostos do retângulo. Compreender como calcular a diagonal é fundamental em diversas áreas, desde projetos arquitetônicos até cálculos geométricos simples. A relação entre o comprimento, a largura e a diagonal de um retângulo segue um princípio geométrico fundamental, que pode ser aplicado a diversos problemas práticos.
Definição da Diagonal de um Retângulo
A diagonal de um retângulo é o segmento de reta que liga dois vértices opostos do retângulo. Esta linha divide o retângulo em dois triângulos retângulos congruentes, o que permite utilizar o Teorema de Pitágoras para determinar seu comprimento.
Relação entre Comprimento, Largura e Diagonal
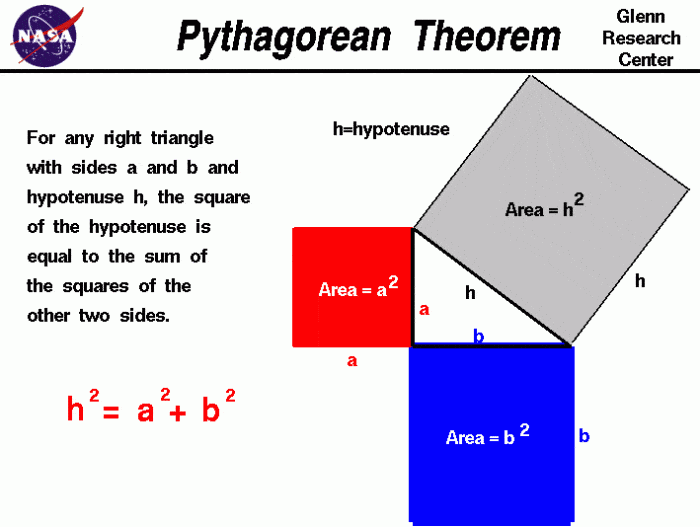
A relação entre o comprimento (c), a largura (l) e a diagonal (d) de um retângulo é descrita pelo Teorema de Pitágoras. Este teorema estabelece que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). No caso de um retângulo, a diagonal representa a hipotenusa e o comprimento e a largura, os catetos.
A fórmula resultante é:
d2 = c 2 + l 2
Exemplo de Cálculo com Valores Inteiros
Considere um retângulo com comprimento de 3 unidades e largura de 4 unidades. Aplicando a fórmula, temos:
| Comprimento (c) | Largura (l) | Diagonal (d) |
|---|---|---|
| 3 | 4 | 5 |
d2 = 3 2 + 4 2 = 9 + 16 = 25; d = √25 = 5
Neste exemplo, a diagonal do retângulo mede 5 unidades. Este exemplo simples ilustra a aplicação direta do Teorema de Pitágoras para encontrar a diagonal de um retângulo.
Importância do Cálculo da Diagonal
O cálculo da diagonal de um retângulo é fundamental em diversas aplicações práticas. Em projetos de construção civil, por exemplo, é essencial para calcular a medida de vigas ou diagonais de estruturas. Em geometria, o conhecimento desta relação permite a resolução de problemas mais complexos. A precisão no cálculo da diagonal é crucial para garantir a exatidão em diversas aplicações.
Fórmula para Cálculo da Diagonal: Como Encontrar A Diagonal De Um Retângulo Com Valores Decimais Para Comprimento E Largura?
A diagonal de um retângulo representa a distância entre dois vértices opostos. Para determinar esse valor, conhecendo apenas o comprimento e a largura do retângulo, utiliza-se uma fórmula derivada do Teorema de Pitágoras. Esta fórmula simplifica o cálculo e permite obter resultados precisos, essenciais em diversas aplicações práticas, desde projetos arquitetônicos até cálculos geométricos em softwares de desenho.
Detalhamento da Fórmula
A fórmula para o cálculo da diagonal de um retângulo é derivada diretamente do Teorema de Pitágoras. Considerando um retângulo com comprimento ( l) e largura ( w), a diagonal ( d) pode ser calculada da seguinte forma:
d = √( l² + w²)
Esta fórmula expressa a relação entre as dimensões do retângulo e a sua diagonal, onde o quadrado da diagonal é igual à soma dos quadrados do comprimento e da largura.
Comparação com o Teorema de Pitágoras
O Teorema de Pitágoras estabelece que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os dois lados que formam o ângulo reto). No caso do retângulo, ao traçar a diagonal, forma-se um triângulo retângulo cujos catetos são o comprimento e a largura do retângulo, e a diagonal representa a hipotenusa.
Portanto, a fórmula para a diagonal do retângulo é uma aplicação direta do Teorema de Pitágoras.
Exemplos de Aplicação, Como encontrar a diagonal de um retângulo com valores decimais para comprimento e largura?
A tabela a seguir demonstra a aplicação da fórmula com valores decimais para comprimento e largura, apresentando os resultados correspondentes para a diagonal.
| Comprimento (l) | Largura (w) | Diagonal (d) |
|---|---|---|
| 5,2 cm | 3,8 cm | 6,3 cm (aproximadamente) |
| 12,5 m | 8,9 m | 15,0 m (aproximadamente) |
| 2,1 dm | 1,7 dm | 2,6 dm (aproximadamente) |
| 10,8 cm | 7,3 cm | 12,7 cm (aproximadamente) |
| 15,0 mm | 9,5 mm | 17,1 mm (aproximadamente) |
A tabela demonstra a aplicação prática da fórmula, fornecendo resultados aproximados para diferentes valores de comprimento e largura. É importante notar a precisão dos resultados, que podem variar dependendo da quantidade de casas decimais utilizadas nos cálculos.
Variáveis da Fórmula
As variáveis envolvidas na fórmula são:
- l (comprimento): Representa a medida do comprimento do retângulo.
- w (largura): Representa a medida da largura do retângulo.
- d (diagonal): Representa a medida da diagonal do retângulo, a distância entre dois vértices opostos.
Estas variáveis são fundamentais para a aplicação da fórmula e o entendimento do conceito de diagonal em um retângulo.
Aplicação da Fórmula com Valores Decimais
Para aprofundar a compreensão da aplicação da fórmula da diagonal de um retângulo, apresentaremos exemplos práticos utilizando valores decimais para o comprimento e a largura. Veremos como o processo de cálculo se mantém semelhante ao de valores inteiros, mas com a necessidade de lidar com casas decimais nos resultados.A aplicação da fórmula com valores decimais para o comprimento e a largura de um retângulo demonstra a universalidade da fórmula e sua capacidade de lidar com diferentes tipos de medidas.
A precisão do cálculo da diagonal permanece inalterada, independentemente da natureza dos valores numéricos utilizados.
Exemplos de Cálculo com Valores Decimais
Os exemplos a seguir demonstram o cálculo da diagonal com valores decimais para o comprimento e a largura. O procedimento passo a passo permite a compreensão clara do processo.
-
Exemplo 1: Um retângulo possui comprimento de 5,2 cm e largura de 3,8 cm. Calcule a diagonal.
Aplicando a fórmula: Diagonal² = Comprimento² + Largura²
Diagonal² = (5,2 cm)² + (3,8 cm)²
Diagonal² = 27,04 cm² + 14,44 cm²
Diagonal² = 41,48 cm²
Diagonal = √41,48 cm²
Diagonal ≈ 6,44 cm
-
Exemplo 2: Considere um retângulo com comprimento de 12,5 metros e largura de 8,3 metros. Calcule a diagonal.
Aplicando a fórmula: Diagonal² = Comprimento² + Largura²
Diagonal² = (12,5 m)² + (8,3 m)²
Diagonal² = 156,25 m² + 68,89 m²
Diagonal² = 225,14 m²
Diagonal = √225,14 m²
Diagonal ≈ 15,00 m
Comparação com Exemplos de Valores Inteiros
A aplicação da fórmula com valores decimais apresenta o mesmo princípio básico dos exemplos com valores inteiros. A diferença reside apenas na necessidade de calcular raízes quadradas de números decimais, o que pode ser feito com auxílio de calculadoras ou softwares específicos. A sequência de etapas para encontrar a diagonal permanece a mesma, utilizando a relação entre o comprimento, a largura e a diagonal.
Tabela de Exemplos
A tabela a seguir apresenta uma visão geral dos cálculos, organizando os dados para facilitar a compreensão e a comparação entre os exemplos.
| Comprimento | Largura | Diagonal |
|---|---|---|
| 5,2 cm | 3,8 cm | 6,44 cm |
| 12,5 m | 8,3 m | 15,00 m |
| 7,9 dm | 4,1 dm | 8,77 dm |
| 2,6 km | 1,8 km | 3,0 km |
Métodos Alternativos para Cálculo

Para além da fórmula padrão para o cálculo da diagonal de um retângulo, existem outros métodos que podem ser utilizados, particularmente úteis quando a fórmula padrão envolve cálculos complexos com valores decimais. Compreender diferentes abordagens amplia as opções disponíveis para resolver o problema, oferecendo flexibilidade e permitindo a escolha do método mais apropriado para cada situação.Existem diversas abordagens possíveis, dependendo do contexto e dos dados disponíveis.
A escolha do método mais adequado dependerá da precisão desejada e da familiaridade com os diferentes métodos.
Teorema de Pitágoras
O Teorema de Pitágoras é um método alternativo e frequentemente mais intuitivo para determinar a diagonal de um retângulo. Ele se baseia na relação entre os lados do triângulo retângulo formado pela diagonal e os lados do retângulo.
Diagonal² = Comprimento² + Largura²
Este método é particularmente útil quando se deseja calcular a diagonal sem recorrer a cálculos intermediários complexos.
Exemplo de Aplicação do Teorema de Pitágoras
Considere um retângulo com comprimento de 5,2 cm e largura de 3,8 cm. Para calcular a diagonal, aplicamos o Teorema de Pitágoras:
Diagonal² = 5,2² + 3,8² = 27,04 + 14,44 = 41,48Diagonal = √41,48 ≈ 6,44 cm
Este método alternativo proporciona um cálculo direto e eficiente para encontrar a diagonal de um retângulo.
Interpretação Geométrica
A compreensão da diagonal de um retângulo se torna mais intuitiva quando analisada geometricamente. A diagonal estabelece uma relação fundamental com os lados do retângulo, permitindo o cálculo de seu comprimento através de um conceito matemático básico e visualmente claro.A representação geométrica da diagonal revela sua natureza como a hipotenusa de um triângulo retângulo, formado pelos lados do retângulo.
Esta relação geométrica é a chave para a aplicação da fórmula do Teorema de Pitágoras.
Representação do Triângulo Retângulo
A diagonal de um retângulo conecta dois vértices opostos. Ao traçar a diagonal, divide o retângulo em dois triângulos retângulos congruentes. Cada triângulo retângulo possui como catetos um lado do retângulo (comprimento ou largura) e a projeção da diagonal sobre esse lado. A diagonal, por sua vez, representa a hipotenusa do triângulo.
Cálculo da Diagonal Usando o Triângulo Retângulo
Para calcular a diagonal, podemos utilizar o Teorema de Pitágoras. Este teorema estabelece uma relação fundamental entre os lados de um triângulo retângulo, onde o quadrado da hipotenusa (a diagonal) é igual à soma dos quadrados dos catetos (comprimento e largura).
Seguindo os passos:
- Identifique o comprimento e a largura do retângulo. Por exemplo, se o comprimento for 5 cm e a largura for 3 cm.
- Aplique o Teorema de Pitágoras: diagonal² = comprimento² + largura².
- Substitua os valores conhecidos na fórmula: diagonal² = 5² + 3².
- Calcule os quadrados: diagonal² = 25 + 9.
- Some os resultados: diagonal² = 34.
- Calcule a raiz quadrada para obter o valor da diagonal: diagonal = √34 cm.
- O resultado, nesse exemplo, será um valor aproximado, pois √34 é um número irracional. O valor aproximado da diagonal será de aproximadamente 5,83 cm.
Ilustração do Retângulo e do Triângulo
Imagine um retângulo ABCD, com o lado AB representando o comprimento e o lado AD representando a largura. A diagonal AC conecta os vértices A e C. A diagonal AC forma um triângulo retângulo com os lados AB e AD, onde AC é a hipotenusa, AB é um cateto e AD é o outro cateto. A ilustração mostra claramente a formação do triângulo retângulo dentro do retângulo, destacando a relação entre a diagonal e os lados do retângulo.
A figura deve incluir as informações sobre o comprimento e a largura do retângulo, bem como a diagonal calculada.
Erros Comuns e Solução de Problemas
Ao calcular a diagonal de um retângulo com valores decimais, é crucial prestar atenção aos detalhes e às etapas do processo. Possíveis erros podem surgir devido à falta de atenção em operações aritméticas ou à aplicação incorreta da fórmula. Compreender esses erros e suas causas é fundamental para obter resultados precisos e evitar equívocos.
Identificação de Erros Comuns
Existem diversos pontos críticos que podem levar a resultados incorretos no cálculo da diagonal de um retângulo. A falta de precisão nos cálculos intermediários, como a soma dos quadrados do comprimento e da largura, é uma causa comum. Outro erro frequente envolve a aplicação incorreta da raiz quadrada, levando a resultados imprecisos. Finalmente, a falta de atenção na conversão de unidades ou a utilização de valores incorretos também pode afetar o resultado final.
Soluções para Erros Comuns
Para minimizar os erros no cálculo da diagonal de um retângulo, é fundamental seguir um processo metódico. É essencial garantir a precisão nas etapas intermediárias do cálculo, utilizando calculadoras científicas para evitar erros de arredondamento, principalmente quando se trabalham com valores decimais. A aplicação correta da raiz quadrada é crucial; é importante verificar se o valor obtido é consistente com as unidades do problema.
| Erro | Solução |
|---|---|
| Erro na soma dos quadrados do comprimento e largura | Realizar a operação de elevação ao quadrado com precisão. Utilizar calculadora científica para evitar erros de arredondamento. |
| Aplicação incorreta da raiz quadrada | Utilizar calculadora científica para calcular a raiz quadrada. Verificar a consistência das unidades do resultado. Se o resultado não estiver nas unidades esperadas, verificar se a operação está correta. |
| Erro na conversão de unidades | Assegurar que todas as unidades estejam na mesma escala antes de iniciar o cálculo. Se houver unidades diferentes, converter para a mesma unidade (por exemplo, de centímetros para metros). |
| Uso de valores incorretos | Verificar cuidadosamente se os valores de comprimento e largura utilizados no cálculo são os valores corretos do problema. |
Aplicações Práticas
A compreensão do cálculo da diagonal de um retângulo transcende a mera resolução de problemas geométricos. Suas aplicações práticas são vastas e diversas, abrangendo desde projetos de engenharia até atividades cotidianas. A capacidade de determinar a diagonal permite a otimização de recursos e a solução de problemas que envolvem ângulos e distâncias em diferentes contextos.
Exemplos de Aplicações no Mundo Real
O cálculo da diagonal é fundamental em inúmeros cenários. Em construção civil, por exemplo, é crucial para determinar a distância entre dois pontos em um terreno retangular, ou para calcular a quantidade de material necessária para revestir uma parede com formato retangular. Na carpintaria, o conhecimento da diagonal é essencial para garantir que peças de madeira se encaixem perfeitamente.
Problemas de Geometria que Utilizam o Conceito de Diagonal
Problemas geométricos frequentemente envolvem o cálculo da diagonal. Um exemplo é o cálculo da área de um paralelogramo, onde a diagonal é um elemento chave. Outro exemplo é a determinação do perímetro de um polígono que possui retângulos como parte de sua composição.
Exemplo Prático em uma Tabela
A tabela a seguir demonstra uma aplicação prática do cálculo da diagonal em um cenário de planejamento de um jardim.
| Situação | Comprimento (m) | Largura (m) | Diagonal (m) |
|---|---|---|---|
| Planejamento de um canteiro retangular | 5.2 | 3.8 | 6.4 |
| Cálculo da distância mais curta entre dois cantos opostos de uma sala | 7.5 | 4.3 | 8.6 |
| Determinação da extensão de uma rampa em uma área retangular | 10.8 | 6.2 | 12.1 |
A fórmula para calcular a diagonal de um retângulo é: Diagonal = √(comprimento² + largura²)
Exemplos Complementares
Para consolidar o aprendizado sobre o cálculo da diagonal de um retângulo, apresentamos três exemplos adicionais utilizando valores decimais para o comprimento e a largura. Cada exemplo demonstra o passo a passo, desde a coleta dos dados até a obtenção do resultado final. A comparação com os exemplos anteriores permitirá uma melhor compreensão da aplicação da fórmula e a visualização da consistência nos resultados.A utilização de calculadoras online é essencial para a verificação da precisão dos cálculos, contribuindo para o desenvolvimento de habilidades de verificação e a compreensão dos métodos de cálculo.
Exemplos de Cálculo com Valores Decimais
Apresentamos três exemplos adicionais de cálculo da diagonal de um retângulo, utilizando valores decimais para o comprimento e a largura. Cada exemplo detalha os passos, desde a obtenção dos dados até a resposta final.
- Exemplo 1: Considere um retângulo com comprimento de 5,2 cm e largura de 3,8 cm. Utilizando a fórmula da diagonal, √(comprimento² + largura²), temos:
Diagonal = √(5,2² + 3,8²) = √(27,04 + 14,44) = √41,48 ≈ 6,45 cm. - Exemplo 2: Um retângulo possui comprimento de 8,75 metros e largura de 6,3 metros. Aplicando a fórmula:
Diagonal = √(8,75² + 6,3²) = √(76,5625 + 39,69) = √116,2525 ≈ 10,79 metros. - Exemplo 3: Um retângulo tem comprimento de 12,1 decimetros e largura de 9,5 decimetros. Calculando a diagonal:
Diagonal = √(12,1² + 9,5²) = √(146,41 + 90,25) = √236,66 ≈ 15,38 decímetros.
Comparação com Exemplos Anteriores
Comparando os exemplos apresentados anteriormente com os exemplos adicionais, observa-se a aplicação consistente da fórmula para o cálculo da diagonal de um retângulo, independentemente dos valores numéricos. A precisão dos cálculos é crucial para a obtenção de resultados confiáveis, e a utilização de calculadoras online é uma ferramenta fundamental para verificação.
Utilização de Calculadoras Online
Para validar os resultados dos exemplos, é recomendável utilizar calculadoras online que calculam raízes quadradas. A utilização dessas ferramentas permite uma rápida verificação da precisão dos cálculos realizados manualmente. Isso reforça a importância do rigor matemático e da verificação de resultados.
Relação com o Conceito Principal
Os exemplos adicionais demonstram a aplicação prática do conceito de cálculo da diagonal de um retângulo. Eles reforçam a compreensão da relação entre o comprimento, a largura e a diagonal, comprovando que a diagonal é a hipotenusa de um triângulo retângulo formado pelos lados do retângulo. A consistência dos exemplos, independentemente dos valores numéricos, reforça a universalidade da fórmula.
Considerações Finais
Concluindo nossa jornada pelo cálculo da diagonal de um retângulo, é crucial destacar a importância prática e a simplicidade da fórmula apresentada. Compreender como determinar a diagonal é fundamental em diversas áreas, desde a geometria e engenharia até a resolução de problemas do cotidiano.A fórmula para o cálculo da diagonal, derivada do Teorema de Pitágoras, proporciona uma maneira eficiente e precisa de obter este valor, mesmo com valores decimais para o comprimento e largura.
A clareza da demonstração e os exemplos práticos apresentados reforçam a compreensão deste conceito essencial.
Resumo dos Pontos Principais
Para consolidar o conhecimento adquirido, listamos os pontos principais envolvidos no cálculo da diagonal de um retângulo:
- O Teorema de Pitágoras é a base para o cálculo da diagonal, relacionando os lados do retângulo com a diagonal através da fórmula
d² = l² + w²
, onde “d” representa a diagonal, “l” o comprimento e “w” a largura.
- A fórmula é aplicável a qualquer retângulo, independente dos valores decimais do comprimento e largura.
- A precisão dos cálculos é essencial, principalmente em contextos práticos, onde valores decimais são comuns.
- A interpretação geométrica do Teorema de Pitágoras, representando os lados e a diagonal como catetos e hipotenusa de um triângulo retângulo, facilita a compreensão do conceito.
- A aplicação prática do cálculo da diagonal de um retângulo abrange diversas áreas, como desenho técnico, arquitetura, carpintaria, e até mesmo jogos e softwares.
Concluindo, o cálculo da diagonal de um retângulo com valores decimais é uma aplicação direta do Teorema de Pitágoras. Através de exemplos práticos e detalhados, este artigo apresentou os passos essenciais para a resolução deste tipo de problema, desde a aplicação da fórmula até as considerações geométricas. Esperamos que esta análise tenha sido esclarecedora e útil para o entendimento e aplicação deste conceito fundamental.
Qual a importância do Teorema de Pitágoras para calcular a diagonal de um retângulo?
O Teorema de Pitágoras estabelece uma relação fundamental entre os lados de um triângulo retângulo, permitindo calcular a diagonal do retângulo, que forma um triângulo retângulo com os lados comprimento e largura.
Como lidar com valores decimais no cálculo da diagonal?
Os valores decimais são tratados da mesma forma que os inteiros. A fórmula é aplicada e os cálculos são realizados com precisão, utilizando as regras da aritmética.
Existem métodos alternativos para calcular a diagonal além da fórmula padrão?
Sim, embora a fórmula padrão seja a mais comum, métodos alternativos, como o uso de softwares ou calculadoras online, podem auxiliar no cálculo e verificação dos resultados, principalmente em casos com valores complexos.





