Relação entre comprimento, largura e diagonal de um retângulo. Esta relação fundamental em geometria, explorada neste artigo, revela a intrincada ligação entre as dimensões de um retângulo e seu elemento diagonal. Compreender essa relação é crucial para diversas aplicações práticas, desde a construção civil até cálculos em carpintaria. A seguir, iremos desvendar as fórmulas matemáticas, as aplicações práticas, as variações e casos especiais, bem como as representações geométricas e gráficas que fundamentam essa relação.
A tabela a seguir ilustra os elementos fundamentais para compreensão da relação entre comprimento, largura e diagonal de um retângulo, apresentando uma organização clara e concisa para facilitar a compreensão.
Introdução à Relação: Relação Entre Comprimento, Largura E Diagonal De Um Retângulo.
Um retângulo é um quadrilátero com quatro ângulos retos. Suas propriedades geométricas são fundamentais em diversas áreas, desde a arquitetura até a engenharia. Compreender a relação entre seu comprimento, largura e diagonal é crucial para cálculos e aplicações práticas.A relação entre comprimento, largura e diagonal de um retângulo é baseada no Teorema de Pitágoras. Este teorema estabelece uma relação fundamental entre os lados de um triângulo retângulo, e o retângulo pode ser visto como formado por dois triângulos retângulos congruentes.
Definição de Termos
O retângulo é um polígono plano com quatro lados, sendo opostos congruentes e paralelos, e quatro ângulos internos retos (90 graus). O comprimento é a medida do lado maior do retângulo, enquanto a largura é a medida do lado menor. A diagonal é o segmento de reta que une dois vértices opostos do retângulo.
Relação entre Comprimento, Largura e Diagonal
A relação entre comprimento, largura e diagonal de um retângulo pode ser expressa através do Teorema de Pitágoras. Se ‘c’ representa o comprimento, ‘l’ a largura e ‘d’ a diagonal, então a relação é expressa pela seguinte equação:
d² = c² + l²
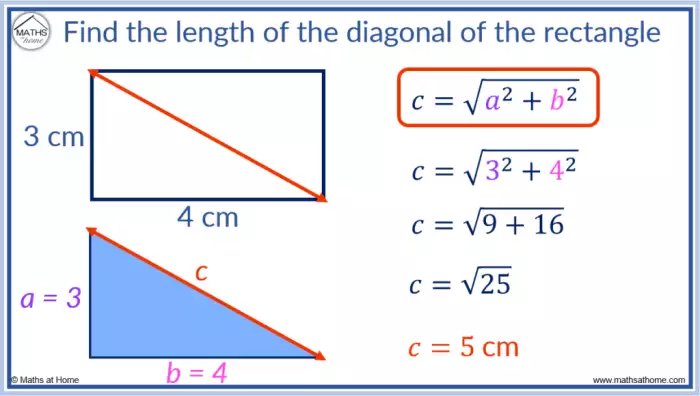
Esta equação permite calcular a diagonal conhecendo o comprimento e a largura, ou vice-versa. Por exemplo, se um retângulo possui comprimento de 3 cm e largura de 4 cm, a diagonal será √(3² + 4²) = √25 = 5 cm.
Tabela de Relação
Esta tabela ilustra a relação entre comprimento, largura e diagonal em diferentes retângulos:
| Comprimento (c) | Largura (l) | Diagonal (d) |
|---|---|---|
| 3 cm | 4 cm | 5 cm |
| 5 cm | 12 cm | 13 cm |
| 8 cm | 6 cm | 10 cm |
A tabela acima demonstra alguns exemplos de retângulos e suas respectivas medidas. Observa-se que a relação entre as medidas é fundamental para a determinação das dimensões do retângulo.
Relação Matemática
A relação entre o comprimento, a largura e a diagonal de um retângulo é fundamental para diversos cálculos geométricos e aplicações práticas. Compreender essa relação permite determinar qualquer um dos três elementos conhecendo os outros dois.A matemática fornece uma fórmula precisa para calcular a diagonal de um retângulo, utilizando o Teorema de Pitágoras. Esta relação, baseada em princípios geométricos, possibilita a solução de problemas em engenharia, arquitetura e outras áreas.
Fórmula da Diagonal
A fórmula que relaciona o comprimento (c), a largura (l) e a diagonal (d) de um retângulo é derivada do Teorema de Pitágoras. Aplicando o teorema a um triângulo retângulo formado pela diagonal, comprimento e largura, obtemos a seguinte relação:
d2 = c 2 + l 2
Esta fórmula demonstra a relação pitagórica entre os lados e a diagonal de um retângulo. A diagonal é a hipotenusa do triângulo retângulo formado pelos lados.
Expressões Alternativas
Existem diferentes formas de expressar a relação entre os elementos, dependendo da variável que se deseja calcular. Para encontrar o comprimento ou a largura, é necessário aplicar a operação inversa, a raiz quadrada.
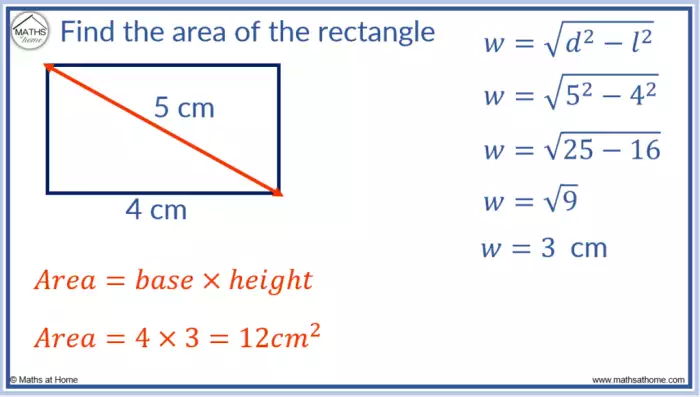
- Para calcular a diagonal (d): d = √(c 2 + l 2)
- Para calcular o comprimento (c): c = √(d 2
-l 2) - Para calcular a largura (l): l = √(d 2
-c 2)
Estas expressões equivalentes são úteis para encontrar qualquer um dos três elementos, desde que os outros dois sejam conhecidos.
Exemplo Numérico
Considere um retângulo com comprimento de 6 cm e largura de 8 cm. Para calcular a diagonal, substituímos os valores na fórmula:
d2 = 6 2 + 8 2 = 36 + 64 = 100
d = √100 = 10 cm
A diagonal do retângulo mede 10 cm.
Tabela de Exemplos
A tabela a seguir apresenta exemplos de cálculo da diagonal, demonstrando a aplicação prática da fórmula.
| Comprimento (cm) | Largura (cm) | Cálculo da Diagonal | Diagonal (cm) |
|---|---|---|---|
| 6 | 8 | √(62 + 82) | 10 |
| 12 | 5 | √(122 + 52) | 13 |
| 10 | 10 | √(102 + 102) | 14,14 |
Aplicações Práticas
A relação entre comprimento, largura e diagonal de um retângulo possui aplicações práticas em diversas áreas, como construção civil, carpintaria, design de interiores, e até mesmo em jogos e cálculos de distâncias. Compreender essa relação permite otimizar projetos e garantir precisão em medições. Esta relação matemática fundamental facilita a resolução de problemas práticos envolvendo geometria.A capacidade de calcular a diagonal de um retângulo é crucial para determinar a distância entre dois pontos opostos, como calcular o comprimento de uma escada apoiada em uma parede ou a distância entre dois cantos opostos de uma sala retangular.
Em projetos de construção, por exemplo, a diagonal pode ser usada para calcular o comprimento de vigas, o ângulo de inclinação de telhados e o posicionamento preciso de materiais.
Construção Civil
A aplicação mais evidente da relação em projetos de construção é a determinação da diagonal. Imagine a necessidade de calcular o comprimento de uma viga que se estende entre dois pontos opostos de uma parede retangular. Conhecendo o comprimento e a largura da parede, a fórmula permite calcular a diagonal, garantindo o corte preciso da viga.
Exemplos de Cálculo da Diagonal
Considere um projeto de construção de um banheiro com 2 metros de largura e 3 metros de comprimento. Para calcular a diagonal, podemos utilizar o Teorema de Pitágoras, que é uma aplicação da relação entre comprimento, largura e diagonal. A fórmula é: diagonal² = comprimento² + largura².
Exemplo Detalhado de Aplicação em Projeto de Construção
Imagine um projeto para a construção de um telhado. A inclinação do telhado deve ser de 30 graus. A largura do telhado é de 5 metros. Para determinar o comprimento da estrutura do telhado, precisamos calcular a diagonal. Sabendo a inclinação, podemos utilizar trigonometria para obter a relação entre a diagonal e a largura.
Cálculo Detalhado (Código HTML)
<div>
<p>Cálculo da diagonal de um retângulo</p>
<p>Comprimento: 5 metros</p>
<p>Largura: 3 metros</p>
<p>Diagonal² = Comprimento² + Largura²</p>
<p>Diagonal² = 5² + 3²</p>
<p>Diagonal² = 25 + 9</p>
<p>Diagonal² = 34</p>
<p>Diagonal = √34 metros</p>
<p>Diagonal ≈ 5,83 metros</p>
</div>
A fórmula para calcular a diagonal de um retângulo, baseada no Teorema de Pitágoras, é: diagonal² = comprimento² + largura².
Variações e Casos Especiais
A relação entre comprimento, largura e diagonal de um retângulo é fundamental para diversas aplicações práticas. Entender como essa relação se modifica em casos específicos, como o do quadrado, e como ela responde a mudanças nos valores de comprimento e largura, é crucial para a compreensão e aplicação correta dos princípios envolvidos. Neste tópico, aprofundaremos a discussão sobre esses aspectos.
Um entendimento detalhado das variações e casos especiais permite a resolução de problemas mais complexos e a aplicação da relação em contextos práticos, como engenharia, arquitetura e design. A compreensão das particularidades do quadrado, por exemplo, simplifica consideravelmente o cálculo da diagonal, o que tem implicações significativas em diversos campos de estudo.
Caso do Quadrado
O quadrado é um caso particular de retângulo, onde os lados possuem a mesma medida. Neste caso específico, a relação entre comprimento, largura e diagonal se simplifica consideravelmente. A diagonal de um quadrado pode ser calculada utilizando o Teorema de Pitágoras, resultando numa relação direta e precisa entre os lados e a diagonal.
Diagonal = Lado
– √2
Esta fórmula demonstra a relação direta entre a diagonal e o lado de um quadrado. Comparando com a fórmula geral para a diagonal de um retângulo, a simplicidade da fórmula do quadrado é evidente. A diagonal de um quadrado é sempre √2 vezes maior que a medida de um dos seus lados.
Comparação com Retângulos Genéricos
A relação entre comprimento, largura e diagonal em um retângulo genérico é mais complexa do que no caso do quadrado. A diagonal é calculada utilizando o Teorema de Pitágoras, considerando os comprimentos dos lados como catetos. A diferença fundamental reside na variação dos valores de comprimento e largura, que afetam diretamente o valor da diagonal.
Diagonal = √(Comprimento² + Largura²)
Esta fórmula demonstra a relação entre os lados e a diagonal em um retângulo genérico. A medida da diagonal é sempre maior que a medida do lado maior do retângulo, mas a relação exata depende da proporção entre comprimento e largura. Quanto maior a diferença entre comprimento e largura, maior a diferença entre a diagonal e o maior lado.
Modificações com Mudanças nos Valores de Comprimento e Largura
A relação entre comprimento, largura e diagonal de um retângulo sofre variações diretamente proporcionais às mudanças nos valores de comprimento e largura. Aumentando ou diminuindo o comprimento e/ou largura, a diagonal também se modifica, mantendo uma relação matemática específica.
A mudança nos valores de comprimento e largura altera a proporção do retângulo, o que, consequentemente, influencia o valor da diagonal. Um aumento no comprimento e largura, por exemplo, resulta em um aumento proporcional na diagonal.
Tabela Comparativa
| Comprimento | Largura | Diagonal | Proporção (C/L) |
|---|---|---|---|
| 10 | 5 | √(10² + 5²) = 11.18 | 2 |
| 8 | 8 | √(8² + 8²) = 11.31 | 1 |
| 12 | 6 | √(12² + 6²) = 13.42 | 2 |
| 15 | 10 | √(15² + 10²) = 18.03 | 1.5 |
A tabela acima demonstra a variação da diagonal em retângulos com diferentes proporções. Observa-se que, para uma mesma proporção, a diagonal cresce proporcionalmente aos lados. No caso do quadrado (proporção 1), a diagonal é sempre √2 vezes maior que o lado.
Relação Geométrica
A relação entre o comprimento, a largura e a diagonal de um retângulo é fundamentalmente geométrica, encontrando sua base nos princípios da geometria euclidiana. Compreender essa relação permite resolver problemas práticos e aplicar conceitos matemáticos em diversas áreas. A diagonal do retângulo, como segmento de reta que conecta dois vértices opostos, estabelece uma ligação crucial entre os lados do retângulo.
A relação geométrica entre os três elementos, comprimento, largura e diagonal, pode ser visualizada e demonstrada através do Teorema de Pitágoras. Este teorema, um pilar da geometria euclidiana, estabelece uma relação fundamental entre os lados de um triângulo retângulo.
Teorema de Pitágoras
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). No caso de um retângulo, a diagonal atua como a hipotenusa de um triângulo retângulo formado pelos lados do retângulo.
c² = a² + b²
Onde:
- c representa o comprimento da diagonal;
- a representa o comprimento do retângulo;
- b representa a largura do retângulo.
Geometria Euclidiana
A geometria euclidiana, desenvolvida por Euclides, é um sistema axiomático que descreve as propriedades do espaço e das figuras geométricas. A relação entre comprimento, largura e diagonal de um retângulo é um exemplo direto da aplicação dos conceitos da geometria euclidiana, especialmente o Teorema de Pitágoras. Os axiomas e teoremas da geometria euclidiana fornecem as ferramentas para demonstrar e aplicar a relação geométrica entre os elementos.
Relação entre os Elementos, Relação entre comprimento, largura e diagonal de um retângulo.
A relação geométrica entre comprimento, largura e diagonal de um retângulo é definida pela aplicação do Teorema de Pitágoras. A diagonal conecta dois vértices opostos do retângulo, formando um triângulo retângulo com os lados do retângulo como catetos e a diagonal como hipotenusa. Esta relação permite calcular qualquer um dos três elementos, conhecendo os outros dois.
Ilustração Geométrica
A figura a seguir ilustra um retângulo ABCD, com lados AB e BC medindo, respectivamente, a e b. A diagonal AC é representada como c. A figura demonstra claramente a formação do triângulo retângulo ABC, onde AC é a hipotenusa.
O retângulo ABCD possui lados AB e BC, e a diagonal AC. A diagonal AC é a hipotenusa do triângulo retângulo ABC, com os lados AB e BC como catetos.
Representação Gráfica
A visualização gráfica da relação entre comprimento, largura e diagonal de um retângulo é crucial para compreender e aplicar as propriedades geométricas envolvidas. Ela permite uma interpretação mais intuitiva e facilita a compreensão da variação da diagonal em função das mudanças nas dimensões do retângulo. A representação gráfica permite a identificação de padrões e a extrapolação de resultados para diferentes casos.A representação gráfica da relação entre as três variáveis (comprimento, largura e diagonal) pode ser elaborada em um sistema de coordenadas cartesianas.
O gráfico demonstra como a diagonal varia conforme o comprimento e a largura do retângulo são alterados. Pontos específicos no gráfico correspondem a retângulos particulares, permitindo a visualização da influência de cada variável na diagonal.
Gráfico da Diagonal em Função do Comprimento e Largura
Um gráfico que ilustra a relação entre o comprimento, a largura e a diagonal de um retângulo pode ser apresentado como uma superfície tridimensional. O eixo horizontal representaria o comprimento, o eixo vertical a largura, e a altura representaria o valor da diagonal. Cada ponto da superfície corresponde a um retângulo específico, com sua respectiva diagonal.
Exemplo Gráfico Interativo
Para facilitar a compreensão da relação, um exemplo gráfico interativo em HTML pode ser desenvolvido. O usuário pode ajustar o comprimento e a largura do retângulo utilizando controles deslizantes ou campos de entrada. O gráfico se atualiza dinamicamente, mostrando a diagonal correspondente aos valores inseridos. Esse recurso permite que o usuário explore diferentes retângulos e observe a variação da diagonal em tempo real.
A visualização dinâmica permite a observação dos padrões da relação.
Exemplo de Implementação (Conceitual)
Imagine um gráfico 3D. Os eixos x e y representam o comprimento e a largura do retângulo, respectivamente. O eixo z representa o valor da diagonal. Ao ajustar o comprimento e a largura em controles deslizantes, o gráfico atualiza a diagonal correspondente, permitindo uma visualização dinâmica da relação. A superfície do gráfico demonstra a variação da diagonal em função das dimensões do retângulo.
A inclinação da superfície representa a relação entre a diagonal e as dimensões.
Propriedades Geométricas
Os retângulos, figuras geométricas planas, possuem características específicas que definem sua forma e influenciam diretamente a relação entre seus lados (comprimento e largura) e sua diagonal. Compreender essas propriedades geométricas é fundamental para analisar e calcular a relação entre essas medidas.
Ângulos Retos
Os retângulos são quadriláteros com quatro ângulos internos retos, ou seja, medindo 90 graus cada. Essa característica é crucial na determinação da relação entre os lados e a diagonal. A perpendicularidade dos lados opostos garante uma relação específica entre as medidas.
Lados Paralelos
Os lados opostos de um retângulo são paralelos entre si. Essa propriedade geométrica garante que a distância entre os lados opostos seja constante e influencia diretamente na forma como a diagonal conecta os vértices opostos. A constância da distância entre os lados paralelos é uma condição necessária para a relação entre os lados e a diagonal.
Relação entre Lados e Diagonal
A relação entre o comprimento, a largura e a diagonal de um retângulo é estabelecida pelo Teorema de Pitágoras. Dado um retângulo com comprimento “c” e largura “l”, a diagonal “d” pode ser calculada pela seguinte fórmula:
d2 = c 2 + l 2
. Esta relação matemática demonstra como a diagonal é a hipotenusa de um triângulo retângulo formado pelos lados adjacentes do retângulo.
Outras Propriedades Geométricas
Além das propriedades já mencionadas, os retângulos possuem outras características relevantes à relação entre suas dimensões.
| Propriedade | Descrição |
|---|---|
| Centro de Simetria | O ponto de interseção das diagonais representa o centro de simetria do retângulo. Este ponto é equidistante de todos os vértices, influenciando a forma como as medidas são relacionadas. |
| Bissetriz das Diagonais | As diagonais de um retângulo dividem-se mutuamente ao meio, criando quatro triângulos congruentes. Esta propriedade contribui para a precisão dos cálculos envolvendo a relação entre as medidas. |
| Congruência dos Lados Opostos | Os lados opostos de um retângulo possuem o mesmo comprimento. Essa propriedade simplifica os cálculos envolvendo a relação entre as medidas. |
Técnicas de Cálculo Alternativas
Para além do método tradicional de Pitágoras, existem outras abordagens para calcular a diagonal de um retângulo, cada uma com suas próprias vantagens em termos de precisão e eficiência. Compreender essas alternativas amplia as possibilidades de cálculo e permite escolher a melhor estratégia dependendo do contexto e da disponibilidade de recursos.A escolha do método mais apropriado para o cálculo da diagonal de um retângulo depende de fatores como a precisão desejada, a complexidade dos cálculos envolvidos e a presença de dados adicionais, como as medidas dos lados.
Algumas técnicas, embora mais complexas, podem resultar em maior precisão em situações onde se requer maior exatidão.
Comparação de Métodos para Cálculo da Diagonal
Existem diferentes métodos para calcular a diagonal de um retângulo, cada um com suas próprias características. A comparação desses métodos permite uma avaliação mais profunda de suas vantagens e desvantagens.
- Método de Pitágoras: Este método, baseado no Teorema de Pitágoras, é o mais comum e geralmente o mais simples para calcular a diagonal. Ele se baseia na relação entre os lados do retângulo e a diagonal, formando um triângulo retângulo. A fórmula é direta e intuitiva: diagonal² = comprimento² + largura². A principal vantagem é a sua simplicidade, o que facilita a aplicação em situações cotidianas.
No entanto, sua precisão depende da exatidão das medidas dos lados.
- Método Trigonométrico: Utilizando funções trigonométricas, como seno, cosseno ou tangente, este método pode ser empregado quando se conhecem ângulos específicos relacionados ao retângulo. A escolha do método trigonométrico depende do contexto e das informações disponíveis. Por exemplo, se o ângulo entre um lado e a diagonal for conhecido, a trigonometria fornece uma alternativa eficaz para o cálculo da diagonal. Sua precisão é afetada pela precisão dos dados de ângulo.
- Métodos Numéricos: Técnicas numéricas, como métodos iterativos ou algoritmos de aproximação, podem ser utilizadas para calcular a diagonal quando as medidas dos lados não são exatas ou quando a precisão desejada é muito alta. Métodos como o método da bissecção ou Newton-Raphson podem ser empregados para refinar as aproximações. A precisão depende da escolha do algoritmo e do número de iterações.
São mais adequados para problemas com resultados complexos ou cálculos com medidas incertas.
Eficiência e Precisão dos Métodos
A eficiência e a precisão de cada método dependem da situação específica. O método de Pitágoras é geralmente eficiente para cálculos rápidos, enquanto os métodos trigonométricos e numéricos podem ser mais precisos em situações que exigem maior exatidão.
| Método | Eficiência | Precisão | Aplicabilidade |
|---|---|---|---|
| Pitágoras | Alta | Média | Cálculos simples e rápidos |
| Trigonométrico | Média | Alta (se ângulos precisos) | Quando ângulos são conhecidos |
| Numérico | Baixa (em geral) | Alta | Cálculos complexos ou alta precisão |
Implementação do Método de Pitágoras (Exemplo em HTML)
O método de Pitágoras é o mais direto e frequentemente o mais eficiente para cálculos simples. A implementação deste método em HTML, usando JavaScript, é uma forma de visualizar sua aplicação prática.
diagonal² = comprimento² + largura²diagonal = √(comprimento² + largura²)
<!DOCTYPE html>
<html>
<head>
<title>Cálculo da Diagonal</title>
</head>
<body>
<label for="comprimento">Comprimento:</label>
<input type="number" id="comprimento"><br>
<label for="largura">Largura:</label>
<input type="number" id="largura"><br>
<button onclick="calcularDiagonal()">Calcular</button>
<p id="resultado"></p>
<script>
function calcularDiagonal()
let comprimento = parseFloat(document.getElementById("comprimento").value);
let largura = parseFloat(document.getElementById("largura").value);
let diagonal = Math.sqrt(comprimento
- comprimento + largura
- largura);
document.getElementById("resultado").innerHTML = "Diagonal: " + diagonal.toFixed(2);
</script>
</body>
</html>
Limitantes e Considerações
A relação entre comprimento, largura e diagonal de um retângulo, embora fundamental na geometria, apresenta limitações e situações específicas em que sua aplicação não é direta ou precisa. Compreender esses aspectos é crucial para a utilização correta da relação em diferentes contextos. É fundamental reconhecer que a aplicação da relação depende da precisão dos dados fornecidos e das suposições feitas.
A relação matemática, por si só, não garante a precisão dos resultados quando aplicada a situações práticas. A precisão dos cálculos depende da precisão dos valores medidos para comprimento, largura e, consequentemente, da diagonal. Valores aproximados introduzem erros que podem se acumular, levando a resultados imprecisos. É essencial considerar o nível de precisão requerido para cada aplicação específica.
Limitações da Relação
A relação entre comprimento, largura e diagonal de um retângulo é baseada no Teorema de Pitágoras. Este teorema, por sua vez, pressupõe um triângulo retângulo. A relação só se aplica a figuras que apresentem ângulos retos (90°) entre os lados. Retângulos são figuras geométricas específicas, não aplicáveis a qualquer quadrilátero ou polígono.
Situações em que a Relação Não é Aplicável
A relação entre comprimento, largura e diagonal não é aplicável a figuras que não sejam retângulos, como trapézios, paralelogramos ou quaisquer outras formas geométricas que não apresentem ângulos retos. A relação também não é válida para objetos tridimensionais, como cubos ou paralelepípedos retângulos, onde o conceito de diagonal tem uma dimensão diferente.
Considerações ao Aplicar a Relação em Contextos Diferentes
Ao aplicar a relação em contextos reais, como a construção de estruturas ou a medição de objetos, é crucial considerar as limitações dos instrumentos de medição. Erros de medição podem afetar a precisão do cálculo da diagonal. A utilização de valores arredondados, em contextos de engenharia, pode impactar significativamente o resultado final, necessitando de análises de tolerância e margem de erro.
A utilização de um nível de precisão apropriado para a situação específica é fundamental.
Limitações dos Cálculos com Valores Aproximados
A utilização de valores aproximados para comprimento e largura em cálculos da diagonal leva a resultados aproximados. A margem de erro pode ser determinada e controlada, usando métodos estatísticos, para garantir um resultado aceitável. Um exemplo prático seria a medição de um terreno retangular com instrumentos com uma margem de erro de 0,5 cm. O resultado da diagonal seria aproximado, considerando essa margem de erro.
É importante reconhecer a limitação intrínseca dos cálculos aproximados e ajustar o grau de precisão exigido com base nas necessidades do contexto.
A precisão dos resultados é diretamente proporcional à precisão dos dados de entrada.
Exemplos e Contraexemplos
A compreensão da relação entre comprimento, largura e diagonal de um retângulo é essencial para diversas aplicações práticas. Neste tópico, serão apresentados exemplos que demonstram a validade da relação, bem como contraexemplos que ilustram situações em que a relação não se aplica ou se manifesta de forma distinta. A análise de casos especiais e a apresentação de exemplos práticos em código HTML permitirão uma melhor assimilação dos conceitos.
Exemplos da Relação Válida
A relação fundamental entre comprimento, largura e diagonal de um retângulo é descrita pelo Teorema de Pitágoras. Para retângulos com lados conhecidos, a diagonal pode ser calculada com precisão.
- Considere um retângulo com comprimento de 3 unidades e largura de 4 unidades. Aplicando o Teorema de Pitágoras (diagonal² = comprimento² + largura²), a diagonal será √(3² + 4²) = √25 = 5 unidades. Este exemplo demonstra a validade da relação.
- Outro exemplo: um retângulo com comprimento de 6 cm e largura de 8 cm. A diagonal será √(6² + 8²) = √100 = 10 cm.
Contraexemplos e Casos Especiais
Embora a relação seja válida para retângulos, ela não se aplica a figuras geométricas que não sejam retângulos. Casos especiais, como quadrados (retângulos com lados iguais), também merecem atenção.
- Um triângulo não possui uma relação direta e simples entre seus lados correspondentes à diagonal de um retângulo. A relação entre os lados de um triângulo é determinada por outros teoremas geométricos.
- Um círculo não possui comprimento e largura definidos da mesma forma que um retângulo. O conceito de diagonal também não se aplica diretamente a um círculo.
- Quadrados: Como caso especial, os quadrados são retângulos onde os lados têm a mesma medida. A relação se mantém, mas a fórmula simplifica, pois comprimento e largura são iguais. Por exemplo, um quadrado com lado de 5 cm terá uma diagonal de √(5² + 5²) = √50 = 5√2 cm.
Exemplos Práticos em HTML
A seguir, um exemplo em código HTML que demonstra o cálculo da diagonal de um retângulo.
| Comprimento | Largura | Diagonal |
|---|---|---|
| 3 | 4 | 5 |
| 6 | 8 | 10 |
| 5 | 5 | 5√2 |
“`html
Exemplo 1: Retângulo com comprimento 3 e largura 4.
Diagonal = √(3² + 4²) = 5
Exemplo 2: Retângulo com comprimento 6 e largura 8.
Diagonal = √(6² + 8²) = 10
“`
Em resumo, a relação entre comprimento, largura e diagonal de um retângulo é um conceito fundamental em geometria, com aplicações práticas em diversas áreas. Vimos como a fórmula matemática, baseada no Teorema de Pitágoras, permite calcular a diagonal conhecendo as outras duas dimensões. Exploramos casos especiais, como o quadrado, e as variações na relação conforme as dimensões mudam.
Além disso, analisamos a importância da geometria euclidiana e as propriedades geométricas dos retângulos. Com isso, obtivemos uma compreensão completa e abrangente sobre esta relação.
Qual a fórmula para calcular a diagonal de um retângulo?
A fórmula para calcular a diagonal (d) de um retângulo é dada por d² = c² + l², onde “c” representa o comprimento e “l” a largura.
Existe alguma diferença na relação entre comprimento, largura e diagonal de um retângulo e de um quadrado?
Sim, no quadrado, como os lados são iguais, a fórmula simplifica para d = c√2.
Quais são as aplicações práticas da relação comprimento, largura e diagonal em construção civil?
Essa relação é fundamental para cálculos de inclinação de telhados, medições em estruturas e em projetos que envolvam ângulos e comprimentos.
Como o Teorema de Pitágoras se relaciona com a diagonal de um retângulo?
O Teorema de Pitágoras (a² + b² = c²) é a base matemática para calcular a diagonal de um retângulo, onde “a” e “b” são os lados e “c” é a diagonal.





