Como calcular a diagonal de um retângulo? Este guia completo aborda o cálculo da diagonal de um retângulo, desde a definição do conceito até as aplicações práticas. Compreender as propriedades dos retângulos e o Teorema de Pitágoras é fundamental para dominar esse cálculo. Acompanhe exemplos práticos, casos especiais, como o cálculo da diagonal de um quadrado, e explore as diferentes aplicações em arquitetura, engenharia e design.
A diagonal de um retângulo representa a distância entre dois vértices opostos. O cálculo da diagonal é crucial em diversos contextos, pois permite determinar a medida de um segmento que conecta pontos opostos em um retângulo. Este guia fornecerá as ferramentas necessárias para calcular a diagonal de um retângulo, utilizando o Teorema de Pitágoras e explorando casos especiais.
Introdução ao cálculo da diagonal de um retângulo
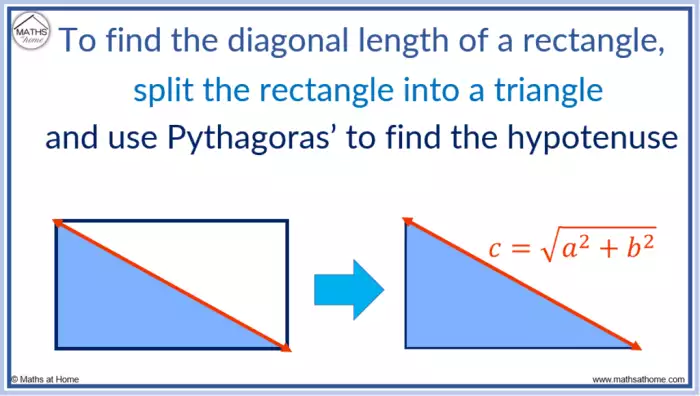
O cálculo da diagonal de um retângulo é uma operação fundamental em geometria, com aplicações práticas em diversas áreas, desde a arquitetura até a engenharia. Compreender como determinar a medida da diagonal é essencial para a resolução de problemas que envolvem figuras retangulares. Este conhecimento permite a obtenção de medidas diagonais em situações diversas, garantindo precisão nos cálculos.A diagonal de um retângulo é o segmento de reta que une dois vértices não adjacentes do retângulo.
A sua importância reside na sua utilização para determinar a distância entre pontos opostos do retângulo, facilitando a visualização e o cálculo de áreas e perímetros. A aplicação prática é evidente em projetos de construção, onde a medição precisa de diagonais é crucial para garantir a forma e as dimensões corretas de estruturas retangulares.
Conceito de Diagonal de um Retângulo
A diagonal de um retângulo é o segmento de reta que liga dois vértices não adjacentes do polígono. Ela divide o retângulo em dois triângulos retângulos congruentes, o que permite o uso do Teorema de Pitágoras para calcular o seu comprimento.
Propriedades Fundamentais do Retângulo
Um retângulo é um quadrilátero com quatro ângulos retos e lados opostos congruentes. Essas propriedades são cruciais para o cálculo da diagonal, pois permitem a aplicação do Teorema de Pitágoras. Lembre-se que os lados opostos de um retângulo são paralelos e congruentes. Esta característica é fundamental para o entendimento do cálculo da diagonal.
Relação entre Lados e Diagonal
O Teorema de Pitágoras estabelece uma relação fundamental entre os lados e a diagonal de um retângulo. Dado um retângulo com lados de comprimento a e b, e uma diagonal de comprimento d, a relação é expressa pela fórmula:
d² = a² + b²
. Essa fórmula permite calcular a diagonal conhecendo os comprimentos dos lados, ou vice-versa. A relação demonstra a conexão direta entre as medidas dos lados e a medida da diagonal.
Tabela Comparativa de Retângulos
A tabela a seguir demonstra como a diagonal varia em função das dimensões dos lados dos retângulos.
| Retângulo | Comprimento (a) | Largura (b) | Diagonal (d) |
|---|---|---|---|
| Retângulo 1 | 3 cm | 4 cm | 5 cm |
| Retângulo 2 | 5 cm | 12 cm | 13 cm |
| Retângulo 3 | 6 cm | 8 cm | 10 cm |
Os valores da tabela ilustram a aplicação prática da fórmula, mostrando como a diagonal aumenta proporcionalmente ao aumento das dimensões dos lados. A precisão nos cálculos garante a exatidão nas medidas, sendo crucial para aplicações práticas.
Métodos para calcular a diagonal
Para determinar a distância entre dois vértices opostos de um retângulo, precisamos de um método eficaz. A diagonal representa essa ligação, e o Teorema de Pitágoras provê a ferramenta ideal para o cálculo. Neste tópico, exploraremos esse método, além de comparar sua eficiência com outros potenciais métodos.
O Teorema de Pitágoras como Método Principal
O Teorema de Pitágoras é fundamental na geometria e, em particular, para calcular a diagonal de um retângulo. Ele estabelece uma relação entre os lados e a hipotenusa de um triângulo retângulo. Em um retângulo, podemos visualizar a diagonal como a hipotenusa de um triângulo retângulo cujos catetos são os lados do retângulo.
Fórmula para o Cálculo da Diagonal
Para calcular a diagonal (d) de um retângulo com lados a e b, utilizamos a seguinte fórmula, derivada do Teorema de Pitágoras:
d = √(a² + b²)
Onde:* d representa o comprimento da diagonal.
a e b representam os comprimentos dos lados do retângulo.
Aplicação Prática do Teorema de Pitágoras
Vamos considerar um exemplo prático. Imagine um retângulo com um lado de 3 cm e outro de 4 cm. Para encontrar a diagonal, aplicamos a fórmula:d = √(3² + 4²)d = √(9 + 16)d = √25d = 5 cmPortanto, a diagonal do retângulo mede 5 cm.
Comparação com Outros Métodos, Como calcular a diagonal de um retângulo
Além do Teorema de Pitágoras, não existem métodos amplamente utilizados para calcular a diagonal de um retângulo. Outras abordagens geométricas podem ser possíveis em casos específicos, mas o Teorema de Pitágoras proporciona uma solução geral e eficiente para a maioria das situações.
Demonstração da Dedução da Fórmula
A fórmula da diagonal (d = √(a² + b²)) é deduzida diretamente do Teorema de Pitágoras. Considere um retângulo com lados a e b. A diagonal forma um triângulo retângulo com os lados a e b como catetos e a diagonal como hipotenusa. O Teorema de Pitágoras afirma que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa, o que resulta na fórmula apresentada.
Exemplos de Cálculo: Como Calcular A Diagonal De Um Retângulo
Para ilustrar o cálculo da diagonal de um retângulo, apresentaremos alguns exemplos práticos. Cada exemplo utilizará diferentes unidades de medida e valores, demonstrando a aplicação da fórmula em situações reais e com valores decimais.A compreensão desses exemplos facilitará a aplicação da fórmula para calcular a diagonal de qualquer retângulo, independentemente das medidas dos seus lados.
Exemplos Numéricos com Diferentes Unidades de Medida
Os exemplos a seguir demonstram o cálculo da diagonal em diferentes retângulos, utilizando centímetros (cm), metros (m) e outras unidades.
- Exemplo 1 (cm): Considere um retângulo com lados medindo 6 cm e 8 cm. Para calcular a diagonal, utilizaremos o Teorema de Pitágoras. A fórmula para calcular a diagonal de um retângulo é a raiz quadrada da soma dos quadrados dos lados.
d = √(a² + b²)
Onde:
– d representa a diagonal.
– a e b representam os lados do retângulo.Seguindo os passos:
- d = √(6² + 8²) = √(36 + 64) = √100
- d = 10 cm
A diagonal do retângulo mede 10 cm.
- Exemplo 2 (m): Um retângulo possui lados de 1,5 m e 2,5 m. Qual o valor da diagonal?
d = √(a² + b²)
Calculando:
- d = √(1,5² + 2,5²) = √(2,25 + 6,25) = √8,5
- d ≈ 2,92 m
A diagonal do retângulo mede aproximadamente 2,92 m.
- Exemplo 3 (ft): Um terreno retangular possui lados de 12 pés e 5 pés. Qual a medida da diagonal?
d = √(a² + b²)
Calculando:
- d = √(12² + 5²) = √(144 + 25) = √169
- d = 13 ft
A diagonal do terreno mede 13 pés.
Exemplos com Valores Decimais
Os exemplos a seguir mostram como aplicar a fórmula com valores decimais.
- Exemplo 4: Um retângulo possui lados de 3,2 cm e 5,8 cm. Calcule a diagonal.
d = √(a² + b²)
- d = √(3,2² + 5,8²) = √(10,24 + 33,64) = √43,88
- d ≈ 6,62 cm
A diagonal do retângulo mede aproximadamente 6,62 cm.
Casos Especiais
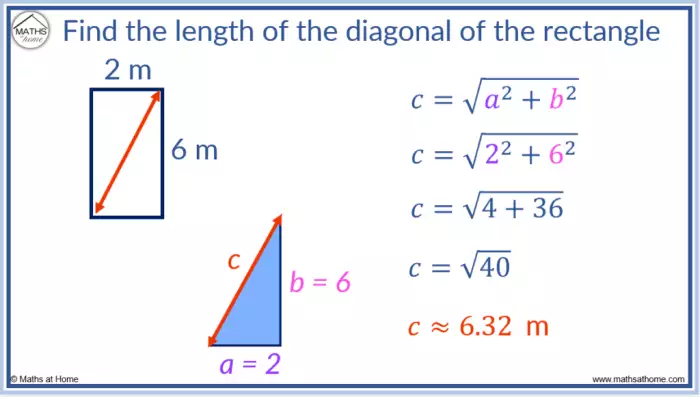
Um caso particular e bastante frequente ao calcular a diagonal de um retângulo é quando o retângulo é, na verdade, um quadrado. Neste caso, a fórmula simplifica-se, tornando o cálculo ainda mais direto e intuitivo. Compreender como a diagonal de um quadrado é calculada em relação à sua forma especial é fundamental para aplicar esses conhecimentos em problemas práticos.
Quadrados: Um Caso Especial de Retângulos
Um quadrado é um caso particular de um retângulo, onde todos os quatro lados possuem a mesma medida. Essa característica singular influencia diretamente no cálculo da diagonal.
Relação entre Lado e Diagonal de um Quadrado
A relação entre o lado e a diagonal de um quadrado é definida pela conhecida relação pitagórica. Imagine um quadrado com lado ‘l’. A diagonal ‘d’ divide o quadrado em dois triângulos retângulos congruentes. Aplicando o Teorema de Pitágoras, podemos estabelecer uma relação direta entre o lado e a diagonal.
d² = l² + l² => d = √(2l²) => d = l√2
A fórmula simplificada para calcular a diagonal de um quadrado é obtida a partir da aplicação do Teorema de Pitágoras, demonstrando a relação direta entre a medida do lado e a medida da diagonal. Note que a diagonal de um quadrado é sempre √2 vezes maior que a medida de seu lado.
Comparação com o Cálculo da Diagonal de um Retângulo Padrão
Para um retângulo padrão, com lados ‘a’ e ‘b’, a fórmula para calcular a diagonal ‘d’ é dada por:
d² = a² + b² => d = √(a² + b²)
Em um quadrado, ‘a’ e ‘b’ são iguais, resultando na simplificação da fórmula para d = l√2. Essa diferença demonstra a particularidade do cálculo para quadrados.
Exemplo de Cálculo em um Quadrado
Se um quadrado possui um lado com medida de 5 cm, sua diagonal será calculada da seguinte forma:
d = 5√2 cm
Este resultado corresponde a aproximadamente 7,07 cm. Este exemplo ilustra a aplicação da fórmula simplificada para o caso específico de um quadrado.
Aplicações Práticas
O cálculo da diagonal de um retângulo, aparentemente um conceito geométrico, possui aplicações práticas em diversas áreas, desde a arquitetura até o design de produtos. Compreender como calcular a diagonal permite resolver problemas concretos e otimizar projetos. A precisão neste cálculo é crucial para garantir a adequação e a funcionalidade dos elementos envolvidos.A aplicação do teorema de Pitágoras, a base para o cálculo da diagonal, permite a determinação da distância entre dois pontos opostos em um retângulo.
Essa distância, representada pela diagonal, é fundamental em situações onde a dimensão total, ou a inclinação, precisa ser considerada.
Aplicações em Arquitetura e Engenharia
O cálculo da diagonal é essencial em projetos arquitetônicos e de engenharia civil para determinar comprimentos de vigas, inclinações de telhados, e dimensões de espaços. Por exemplo, ao projetar uma escada, é crucial calcular a diagonal do vão para determinar o comprimento da rampa e a inclinação adequada. A diagonal também auxilia no cálculo da área de cobertura e na verificação da estabilidade de estruturas.
Aplicações em Design de Produtos
O conhecimento do cálculo da diagonal é útil na concepção de produtos com formas retangulares ou que envolvam ângulos retos. Em design de móveis, por exemplo, o cálculo da diagonal é fundamental para o projeto de peças com bases retangulares e inclinações específicas. No desenvolvimento de displays ou painéis retangulares, a diagonal influencia a escolha da resolução e do tamanho ideal para o produto.
Aplicações em Projetos de Design Gráfico
Em projetos gráficos, o cálculo da diagonal auxilia na composição visual e na disposição dos elementos. A diagonal pode ser usada para criar um efeito de profundidade, direção e movimento na imagem, impactando a percepção do espectador. Um bom exemplo é a utilização de diagonais para a estruturação de layouts em design de sites e revistas.
Situações onde é necessário calcular a diagonal
A diagonal de um retângulo é necessária em inúmeras situações, das mais simples às mais complexas.
- Projeto de escadas: Para determinar o comprimento da rampa e a inclinação adequada.
- Construção de telhados: Para calcular o comprimento das telhas e a inclinação do telhado.
- Design de móveis: Para projetar peças com bases retangulares e inclinações específicas.
- Construção de estruturas: Para calcular a estabilidade e a resistência de elementos estruturais.
- Design de displays e painéis: Para determinar a resolução e o tamanho ideal do produto.
Comparação da Necessidade em Diferentes Áreas
A necessidade de calcular a diagonal varia de acordo com a área de atuação. Na arquitetura e engenharia, a precisão é crucial para a segurança e a funcionalidade das estruturas. No design de produtos, a diagonal influencia o design estético e a usabilidade do produto. Em design gráfico, a diagonal é uma ferramenta para composição e percepção visual.
Em cada área, a diagonal é um elemento essencial para a resolução de problemas e a criação de soluções eficazes.
Diagramas e Ilustrações
Para compreendermos melhor como calcular a diagonal de um retângulo, é fundamental visualizar a relação geométrica entre os seus lados e a diagonal. Os diagramas e ilustrações tornam o conceito mais acessível e facilitam a compreensão das etapas envolvidas no cálculo. A representação gráfica permite a visualização da aplicação do Teorema de Pitágoras, elemento chave para a determinação da diagonal.Os diagramas e ilustrações apresentados a seguir demonstram, de forma clara e concisa, a aplicação do Teorema de Pitágoras a retângulos de diferentes proporções.
Cada ilustração, acompanhada de uma descrição detalhada, ajuda a consolidar o entendimento da relação entre os lados e a diagonal de um retângulo.
Aplicação do Teorema de Pitágoras em um Retângulo
O Teorema de Pitágoras estabelece uma relação fundamental entre os lados de um triângulo retângulo. Em um retângulo, ao traçarmos a diagonal, formamos dois triângulos retângulos congruentes. A diagonal representa a hipotenusa desses triângulos, e os lados do retângulo correspondem aos catetos. A fórmula do Teorema de Pitágoras, a² + b² = c², pode ser aplicada diretamente para encontrar o valor da diagonal (c), conhecendo os valores dos lados (a e b).
A diagonal de um retângulo é a hipotenusa de um triângulo retângulo cujos catetos são os lados do retângulo.
Ilustrações de Retângulos com Diferentes Proporções
As ilustrações seguintes demonstram a aplicação do Teorema de Pitágoras em retângulos com diferentes proporções. Cada retângulo apresenta seus lados e a diagonal, facilitando a visualização da relação entre as medidas.
- Um retângulo com lados de 3 cm e 4 cm terá uma diagonal de 5 cm.
- Um retângulo com lados de 5 cm e 12 cm terá uma diagonal de 13 cm.
- Um retângulo com lados de 6 cm e 8 cm terá uma diagonal de 10 cm.
- Um retângulo com lados de 7 cm e 24 cm terá uma diagonal de 25 cm.
Estas ilustrações exemplificam a aplicação do Teorema de Pitágoras em situações práticas, onde os lados do retângulo são representados graficamente, bem como a diagonal.
Construção de um Diagrama para o Cálculo da Diagonal
Para construir um diagrama para calcular a diagonal de um retângulo, seguem as etapas:
- Desenhe um retângulo com lados de comprimento ‘a’ e ‘b’.
- Trace a diagonal do retângulo, dividindo-o em dois triângulos retângulos.
- Identifique os catetos como ‘a’ e ‘b’ e a diagonal como ‘c’.
- Aplique o Teorema de Pitágoras: a² + b² = c².
- Resolva a equação para encontrar o valor de ‘c’.
Estas etapas detalhadas demonstram como construir um diagrama e aplicar o Teorema de Pitágoras para encontrar a diagonal de um retângulo.
Relação Geométrica entre os Lados e a Diagonal
A relação geométrica entre os lados e a diagonal de um retângulo é descrita pelo Teorema de Pitágoras. O quadrado da diagonal é igual à soma dos quadrados dos lados.
a² + b² = c²
onde:
- a e b são os comprimentos dos lados do retângulo.
- c é o comprimento da diagonal.
Este esquema ilustra a relação fundamental entre as medidas dos lados e da diagonal de um retângulo.
Fórmulas Alternativas (se aplicável)
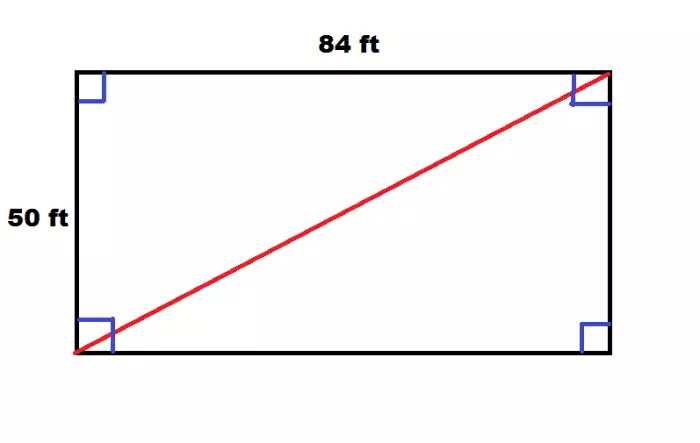
Para além da fórmula mais comum para o cálculo da diagonal de um retângulo, existem outras abordagens possíveis, dependendo das informações disponíveis. Essas fórmulas alternativas podem simplificar o cálculo em determinadas situações. Compreender essas diferentes opções permite uma maior flexibilidade na resolução de problemas relacionados à geometria.Existem situações em que aplicar fórmulas alternativas pode ser mais eficiente do que utilizar a fórmula principal, especialmente quando já se conhecem valores específicos, como a área ou um dos lados do retângulo.
O entendimento das condições de aplicação e das vantagens/desvantagens de cada fórmula alternativa torna o processo de resolução mais estratégico.
Relação entre Diagonal, Área e Lados
Compreender a relação entre a diagonal, a área e os lados de um retângulo permite explorar fórmulas alternativas. Se conhecemos a área e um dos lados, podemos determinar o outro lado e, consequentemente, a diagonal.
- Se a área (A) e um dos lados (l) do retângulo são conhecidos, a fórmula para o cálculo do outro lado (L) é L = A/l. Conhecendo L e l, podemos calcular a diagonal (d) usando a fórmula de Pitágoras, d² = l² + L².
Exemplo de Aplicação
Considere um retângulo com área de 24 cm² e um lado com 4 cm de comprimento. Para encontrar o outro lado, dividimos a área pelo lado conhecido: L = 24 cm²/4 cm = 6 cm. Aplicando a fórmula de Pitágoras, encontramos a diagonal: d² = 4² + 6² = 16 + 36 = 52. Portanto, d = √52 cm ≈ 7,21 cm.
Fórmula Utilizando o Teorema de Pitágoras
O Teorema de Pitágoras é fundamental para o cálculo da diagonal. A fórmula principal, d² = l² + L², é uma aplicação direta desse teorema em um triângulo retângulo formado pela diagonal e os lados do retângulo.
d² = l² + L²
Essa fórmula é universalmente aplicável, pois qualquer retângulo pode ser decomposto em um triângulo retângulo com a diagonal como hipotenusa.
Considerações sobre Vantagens e Desvantagens
As fórmulas alternativas, baseadas na área e em um dos lados, podem ser mais convenientes se esses valores forem previamente conhecidos. No entanto, a fórmula principal, usando os dois lados, é mais direta e geralmente mais fácil de aplicar. A escolha da fórmula dependerá dos dados disponíveis.
Erros Comuns e Solução
Os cálculos da diagonal de um retângulo, embora geralmente simples, podem apresentar erros se não forem seguidos os passos corretos. Compreender os erros comuns e suas causas permite uma resolução mais eficaz e garante resultados precisos. Este tópico detalha os possíveis erros e oferece soluções para evitar e corrigir tais problemas.A precisão nos cálculos geométricos é fundamental em diversas áreas, desde projetos de engenharia até aplicações cotidianas.
Identificar e corrigir erros precocemente evita problemas mais complexos e garante a confiabilidade dos resultados.
Identificação de Erros na Medição
As medidas dos lados do retângulo são a base para o cálculo da diagonal. Erros na medição podem levar a resultados incorretos. É crucial garantir que as medidas estejam corretas, utilizando instrumentos de medição calibrados e técnicas adequadas. A utilização de instrumentos imprecisos ou a falta de atenção durante a medição são causas comuns de erros. Para garantir precisão, utilize instrumentos de medição precisos e realize medições múltiplas, verificando a consistência dos valores.
Erros na Aplicação da Fórmula
A fórmula para calcular a diagonal de um retângulo, √(lado1² + lado2²), é crucial. Erros na aplicação desta fórmula podem levar a resultados incorretos. É importante garantir que os valores corretos dos lados do retângulo sejam substituídos na fórmula, bem como que as operações matemáticas sejam executadas corretamente. Um erro comum é esquecer de elevar os lados ao quadrado ou realizar a operação de raiz quadrada de forma incorreta.
Para evitar este tipo de erro, é fundamental verificar a fórmula passo a passo, garantindo que cada etapa esteja correta. Recomenda-se anotar os passos do cálculo para facilitar a verificação.
Erros de Cálculo
√(lado1² + lado2²)
Após a substituição dos valores dos lados na fórmula, os cálculos devem ser realizados com precisão. Erros aritméticos, como erros na adição, subtração, multiplicação ou divisão, podem levar a resultados incorretos. Erros de arredondamento, ao usar aproximações, também podem afetar a precisão. Para minimizar erros de cálculo, utilize uma calculadora científica ou uma ferramenta de cálculo online, garantindo que os cálculos sejam feitos corretamente.
Verifique se a calculadora está configurada para exibir resultados com precisão suficiente.
Dicas para Evitar Erros
- Utilize instrumentos de medição calibrados e confiáveis para garantir medidas precisas dos lados do retângulo.
- Anote os passos do cálculo para facilitar a verificação.
- Substitua os valores dos lados na fórmula com atenção.
- Verifique cuidadosamente cada etapa do cálculo, garantindo que as operações matemáticas estejam corretas.
- Utilize uma calculadora científica ou uma ferramenta de cálculo online para minimizar erros de cálculo.
- Verifique a precisão da calculadora utilizada.
- Arredonde os resultados de forma apropriada, considerando o nível de precisão necessário.
Como Reconhecer e Corrigir Erros
Para reconhecer erros, verifique se as unidades das medidas dos lados estão consistentes. Se o resultado da diagonal for negativo, isso indica um erro no cálculo. Em caso de resultados absurdos ou inconsistentes, reveja todo o processo, verificando cada passo e procurando por possíveis erros. Verifique se as fórmulas foram aplicadas corretamente e se as operações aritméticas foram realizadas de forma correta.
Se o resultado não for plausível, verifique os cálculos e as medidas novamente.
Tabelas e Resumos
As tabelas a seguir resumem as informações essenciais para o cálculo da diagonal de um retângulo, organizando as fórmulas, exemplos, casos especiais e aplicações práticas de forma concisa e acessível. A compreensão dessas tabelas permitirá uma melhor assimilação dos conceitos e facilitará a aplicação prática do conhecimento.
Fórmulas e Métodos para o Cálculo da Diagonal
Esta tabela apresenta as fórmulas e métodos mais comuns para determinar a diagonal de um retângulo.
| Método | Fórmula | Descrição |
|---|---|---|
| Teorema de Pitágoras | d = √(a² + b²) | Onde ‘d’ representa a diagonal, ‘a’ e ‘b’ representam os lados do retângulo. |
Exemplos de Cálculo com Diferentes Resultados
A tabela abaixo ilustra exemplos de cálculos de diagonais com diferentes medidas para os lados do retângulo.
| Retângulo | Lado a (cm) | Lado b (cm) | Diagonal (cm) |
|---|---|---|---|
| Retângulo 1 | 3 | 4 | 5 |
| Retângulo 2 | 5 | 12 | 13 |
| Retângulo 3 | 6 | 8 | 10 |
Etapas para o Cálculo da Diagonal
Esta tabela detalha as etapas para calcular a diagonal de um retângulo, utilizando o Teorema de Pitágoras.
| Etapa | Descrição |
|---|---|
| 1 | Identificar as medidas dos lados do retângulo (a e b). |
| 2 | Substituir os valores de ‘a’ e ‘b’ na fórmula d = √(a² + b²). |
| 3 | Calcular o quadrado de ‘a’ e ‘b’. |
| 4 | Somar os quadrados de ‘a’ e ‘b’. |
| 5 | Calcular a raiz quadrada do resultado da soma. |
| 6 | O resultado obtido é a medida da diagonal do retângulo. |
Casos Especiais de Retângulos
A tabela a seguir apresenta casos especiais de retângulos, como o quadrado, e como calcular a diagonal nesses casos.
| Caso Especial | Características | Fórmula da Diagonal |
|---|---|---|
| Quadrado | Todos os lados possuem a mesma medida. | d = a√2 |
Aplicações Práticas do Cálculo da Diagonal
Esta tabela ilustra algumas aplicações práticas do cálculo da diagonal de um retângulo.
| Aplicação | Descrição |
|---|---|
| Construção | Cálculo de comprimentos de vigas, diagonais de telhados e outros elementos estruturais. |
| Design | Cálculo de diagonais em projetos de móveis, decoração e artes visuais. |
| Engenharia | Determinação de distâncias em projetos de tubulações, instalações elétricas e outros sistemas. |
Ao longo deste guia, exploramos o cálculo da diagonal de um retângulo, abordando diferentes aspectos, desde a teoria até a prática. Apresentamos o Teorema de Pitágoras como ferramenta essencial, e demonstramos como ele se aplica em exemplos práticos, incluindo retângulos com diferentes dimensões e casos especiais, como quadrados. Com exemplos, fórmulas e ilustrações, este guia fornece uma compreensão abrangente do tema, facilitando a aplicação do conhecimento em situações do dia a dia.
Qual a fórmula para calcular a diagonal de um retângulo?
A fórmula para calcular a diagonal (d) de um retângulo com lados a e b é: d = √(a² + b²).
Como o cálculo da diagonal de um retângulo se aplica na arquitetura?
Em arquitetura, o cálculo da diagonal é utilizado em projetos de pisos, paredes e estruturas, para garantir a estabilidade e a precisão das medidas.
Existe diferença no cálculo da diagonal de um retângulo e de um quadrado?
Sim, no quadrado, os lados são iguais (a = b), simplificando a fórmula para d = √(a² + a²) = √2a² = a√2.
Quais são os erros mais comuns ao calcular a diagonal de um retângulo?
Erros comuns incluem a confusão entre os lados e a diagonal, a aplicação incorreta do Teorema de Pitágoras e a utilização de unidades de medida incorretas.





