Dicas e truques para calcular a diagonal de um retângulo de forma eficiente. Este guia aborda o cálculo da diagonal de retângulos, desde a compreensão do conceito fundamental até técnicas avançadas e o uso de ferramentas tecnológicas. Aprofundaremos o Teorema de Pitágoras e exploraremos métodos alternativos, exemplificando sua aplicação em situações práticas e focando em precisão e eficiência.
Compreender como calcular a diagonal de um retângulo é crucial em diversas áreas, desde a geometria até a engenharia. Este conteúdo oferece um panorama completo sobre o assunto, abordando os fundamentos matemáticos e a aplicação prática em cenários reais.
Introdução ao cálculo da diagonal de um retângulo
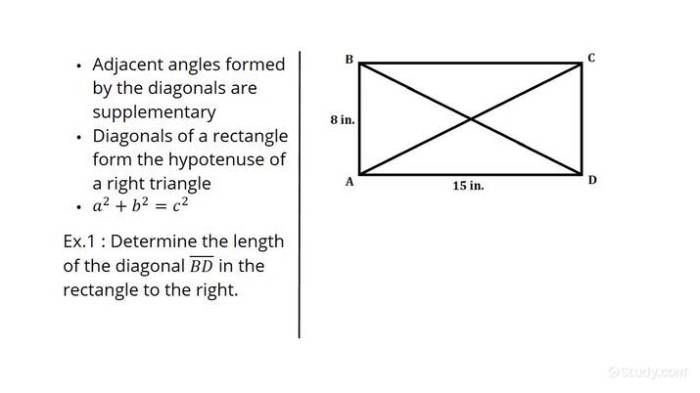
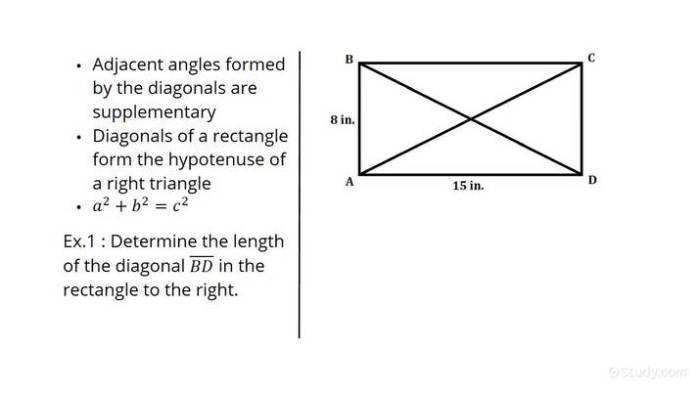
A diagonal de um retângulo é o segmento de reta que une dois vértices opostos do retângulo. Compreender como calcular a diagonal é fundamental em diversas áreas, desde a engenharia até a geometria cotidiana. A aplicação prática vai da construção de estruturas à resolução de problemas em informática e design gráfico, demonstrando a importância da geometria em nosso dia a dia.O cálculo da diagonal de um retângulo se baseia no Teorema de Pitágoras, um conceito matemático de grande importância histórica.
A capacidade de determinar essa medida permite otimizar o uso de materiais, calcular distâncias e garantir a precisão em projetos. Para isso, precisamos entender as variáveis envolvidas: o comprimento e a largura do retângulo.
Variáveis Envolvidas
O cálculo da diagonal de um retângulo depende diretamente do comprimento e da largura do mesmo. Essas medidas são essenciais para aplicar o Teorema de Pitágoras e obter a diagonal.
O Teorema de Pitágoras: Uma Breve História
O Teorema de Pitágoras, atribuído ao matemático grego Pitágoras, descreve a relação entre os lados de um triângulo retângulo. Embora atribuído a ele, a compreensão da relação entre os lados de triângulos retângulos era conhecida por culturas anteriores, como a babilônica. A formulação formal e a demonstração rigorosa, atribuídas a Pitágoras, tornaram-se um marco fundamental na história da matemática, fornecendo uma base para o cálculo de distâncias e comprimentos em diversas situações.
Comparativo entre Tipos de Retângulos
A fórmula para o cálculo da diagonal se mantém consistente, independentemente do tipo de retângulo. No entanto, há particularidades em relação aos quadrados. Um quadrado é um caso especial de retângulo, onde todos os lados têm a mesma medida.
| Tipo de Retângulo | Fórmula da Diagonal | Características |
|---|---|---|
| Retângulo Comum | Diagonal = √(comprimento² + largura²) | Lados opostos iguais e paralelos, ângulos internos retos. |
| Quadrado | Diagonal = √(lado² + lado²) = lado√2 | Todos os lados têm a mesma medida, ângulos internos retos e diagonais congruentes. |
O quadro acima demonstra a relação entre as fórmulas e as características dos retângulos e quadrados, destacando a simplificação da fórmula para o caso específico do quadrado.
O Teorema de Pitágoras
O Teorema de Pitágoras é um princípio fundamental da geometria que estabelece uma relação entre os lados de um triângulo retângulo. Essa relação é crucial para calcular a diagonal de um retângulo, pois a diagonal forma, juntamente com os lados do retângulo, um triângulo retângulo. Compreendendo o teorema, podemos determinar a medida da diagonal com precisão e eficiência.O teorema de Pitágoras afirma que, em qualquer triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados).
Esta relação permite determinar um lado desconhecido quando os outros dois são conhecidos.
Aplicação ao Cálculo da Diagonal
Um retângulo pode ser decomposto em dois triângulos retângulos congruentes, utilizando a sua diagonal como hipotenusa. Aplicando o teorema de Pitágoras, podemos encontrar o comprimento da diagonal.
Passos para a Resolução
Para calcular a diagonal de um retângulo, siga os passos abaixo, utilizando as medidas dos lados do retângulo como catetos:
- Identifique os lados do retângulo como catetos do triângulo retângulo formado pela diagonal.
- Eleve ao quadrado os valores dos lados do retângulo (a e b). Por exemplo, se os lados medem 3 cm e 4 cm, teremos 3² = 9 cm² e 4² = 16 cm².
- Some os quadrados dos catetos obtidos no passo anterior. No exemplo, 9 cm² + 16 cm² = 25 cm².
- Calcule a raiz quadrada da soma obtida no passo anterior. No exemplo, √25 cm² = 5 cm.
- O resultado obtido é o comprimento da diagonal do retângulo.
Fórmula Geral: d = √(a² + b²)
Onde:
d = comprimento da diagonal
a = comprimento de um lado do retângulo
b = comprimento do outro lado do retângulo
Eficiência do Método
O método utilizando o Teorema de Pitágoras é considerado eficiente para o cálculo da diagonal de um retângulo, pois é direto e baseado em um princípio fundamental da geometria. Comparado a métodos alternativos que envolvem trigonometria, por exemplo, o método de Pitágoras é mais simples e requer menos etapas. A simplicidade e a precisão do método o tornam uma ferramenta valiosa para cálculos rápidos e eficazes.
Métodos Alternativos para Cálculo
Além do Teorema de Pitágoras, existem outros métodos para calcular a diagonal de um retângulo, cada um com suas próprias vantagens e desvantagens em termos de precisão e complexidade. Compreender esses métodos alternativos amplia as opções disponíveis para resolver esse problema matemático fundamental.A escolha do método mais adequado dependerá das informações disponíveis e das necessidades específicas da aplicação. Alguns métodos podem ser mais eficientes para cálculos manuais, enquanto outros podem ser mais convenientes em contextos computacionais.
Considerações sobre Precisão e Complexidade
A precisão e a complexidade dos métodos para calcular a diagonal de um retângulo são fatores cruciais a serem considerados. Métodos mais precisos podem exigir cálculos mais complexos, o que pode levar a resultados mais acurados, mas com um custo computacional maior. Métodos mais simples, por outro lado, podem oferecer resultados razoáveis, mas com uma precisão menor, dependendo da aplicação.
Método Utilizando Trigonometria
Este método se baseia na relação entre os lados do retângulo e o ângulo reto. Sabendo os comprimentos dos lados do retângulo, podemos utilizar as funções trigonométricas (seno, cosseno ou tangente) para determinar o valor da diagonal. Este método é útil em contextos onde se conhece um ângulo além dos lados.
Por exemplo, se um retângulo tem lados de 3 cm e 4 cm, o valor da diagonal pode ser calculado usando o Teorema de Pitágoras, resultando em 5 cm. Se o ângulo entre um lado e a diagonal for conhecido, a trigonometria pode ser usada para determinar a diagonal.
Método Utilizando a Relação entre Lados e Diagonal
Este método é uma aplicação direta do Teorema de Pitágoras. A diagonal de um retângulo é a hipotenusa de um triângulo retângulo formado pelos dois lados do retângulo.
A fórmula para calcular a diagonal (d) é: d² = a² + b², onde ‘a’ e ‘b’ são os comprimentos dos lados do retângulo.
Este método é amplamente utilizado devido à sua simplicidade e precisão.
Comparativo dos Métodos
| Método | Passos | Exemplo | Precisão | Complexidade |
|---|---|---|---|---|
| Teorema de Pitágoras | 1. Identificar os lados do retângulo (a e b). 2. Calcular d² = a² + b². 3. Calcular a raiz quadrada de d² para obter d. | Se a = 3 e b = 4, então d² = 3² + 4² = 9 + 16 = 25, logo d = 5. | Alta | Baixa |
| Trigonometria | 1. Identificar os lados do retângulo (a e b) e o ângulo entre um lado e a diagonal. 2. Utilizar a função trigonométrica apropriada (seno, cosseno ou tangente) para determinar a diagonal. | Se a = 3, b = 4 e o ângulo for 45°, então d = a/cos(45°) = b/sen(45°). | Alta | Média |
A tabela acima apresenta um comparativo simplificado dos métodos, destacando suas principais características. A escolha do método mais adequado dependerá da informação disponível e do contexto da aplicação.
Exemplos Práticos e Aplicações
A compreensão teórica do cálculo da diagonal de um retângulo é fundamental, mas a sua aplicação prática em situações do dia a dia torna este conhecimento ainda mais valioso. Neste tópico, serão apresentados exemplos práticos que demonstram como o cálculo da diagonal é utilizado em diversas áreas, desde a construção até a resolução de problemas cotidianos. Além disso, serão propostos exercícios para consolidar os conhecimentos adquiridos.A aplicação do Teorema de Pitágoras para determinar a diagonal de um retângulo é crucial em diversas áreas, desde a engenharia até a geometria diária.
A capacidade de calcular a diagonal permite otimizar processos, projetar estruturas e solucionar problemas que envolvem distâncias em duas dimensões.
Problemas Práticos e Aplicações Diárias
O cálculo da diagonal de um retângulo é essencial em diversas situações do dia a dia, como na construção civil e em projetos de design. Por exemplo, ao construir um cômodo retangular, a diagonal do piso é fundamental para determinar a quantidade de material necessário para o revestimento, ou a distância entre dois pontos opostos.
- Construção de Paredes: Imagine a necessidade de construir uma parede diagonal em um cômodo retangular. Para determinar a quantidade de material necessária, o cálculo da diagonal do cômodo é crucial. A diagonal indica a medida real do espaço a ser coberto, e não apenas a soma das medidas dos lados.
- Design de Móveis: Um designer precisa calcular a diagonal de um painel retangular para determinar o melhor ângulo de inclinação de uma prateleira, ou a capacidade de acomodar objetos em um móvel retangular.
- Navegação: Em um mapa, a diagonal de um retângulo pode representar a distância mais curta entre dois pontos opostos de um terreno retangular. Isso é útil para determinar a melhor rota de viagem.
- Eletrônicos: A diagonal da tela de um televisor ou computador é um parâmetro fundamental para a classificação e comparação dos modelos. Este valor indica a dimensão visual da tela.
Exercícios com Soluções
Para consolidar os conhecimentos, são apresentados alguns exercícios com soluções detalhadas. A resolução de problemas é fundamental para a compreensão prática dos conceitos matemáticos.
| Problema | Solução |
|---|---|
| Um terreno retangular possui 8 metros de largura e 15 metros de comprimento. Qual a medida da diagonal do terreno? | Aplicando o Teorema de Pitágoras (diagonal² = largura² + comprimento²), temos: diagonal² = 8² + 15² = 64 + 225 = 289. Portanto, a diagonal é √289 = 17 metros. |
| Um quadro retangular tem 20 cm de largura e 30 cm de comprimento. Qual a medida da diagonal do quadro? | Aplicando o Teorema de Pitágoras: diagonal² = 20² + 30² = 400 + 900 = 1300. Portanto, a diagonal é √1300 ≈ 36,06 cm. |
Considerações sobre Precisão e Erros
A precisão é fundamental ao calcular a diagonal de um retângulo, pois erros podem levar a resultados incorretos em aplicações práticas. Compreender as fontes potenciais de erro e como avaliá-las é crucial para garantir a confiabilidade dos cálculos. Neste tópico, discutiremos a importância da precisão, as fontes de erro em diferentes métodos de cálculo e como estimar a margem de erro.A precisão no cálculo da diagonal afeta diretamente a exatidão do resultado final.
Pequenos erros nas medidas dos lados do retângulo podem propagar-se e resultar em erros significativos na diagonal calculada. Por exemplo, em projetos de engenharia, arquitetura ou manufatura, uma pequena imprecisão na diagonal pode levar a problemas estruturais ou dimensionais indesejáveis.
Importância da Precisão no Cálculo
A precisão no cálculo da diagonal é vital para garantir a exatidão em diversas aplicações. A confiabilidade dos resultados é essencial para evitar problemas em projetos de engenharia, arquitetura, ou até mesmo em cálculos de áreas de terrenos. Um erro de cálculo pode resultar em custos adicionais ou em problemas de compatibilidade em sistemas.
Fontes de Erro em Cálculos Manuais
Erros em cálculos manuais podem surgir de várias formas. A utilização de aproximações ou arredondamentos incorretos em etapas intermediárias é uma fonte comum de imprecisão. A falta de atenção aos dígitos significativos e à correta utilização de regras de arredondamento pode gerar erros cumulativos. A manipulação manual de valores numéricos também está sujeita a erros de digitação, o que pode levar a resultados totalmente imprecisos.
A exatidão dos cálculos depende fortemente da habilidade e da atenção do operador.
Fontes de Erro em Ferramentas e Softwares
As ferramentas e softwares de cálculo, embora geralmente mais precisos que os cálculos manuais, também podem apresentar erros. A precisão da ferramenta está relacionada à sua capacidade de representar números decimais. Limitações na precisão da representação dos números decimais podem levar a erros de arredondamento, especialmente em cálculos complexos ou com números muito grandes ou muito pequenos. Também é importante verificar se a ferramenta utilizada está configurada para o nível de precisão necessário.
Avaliação da Margem de Erro em Diferentes Métodos
Para avaliar a margem de erro em diferentes métodos de cálculo, é necessário considerar as fontes de erros inerentes a cada método. Em cálculos manuais, a margem de erro depende da precisão das medidas dos lados do retângulo e das operações aritméticas realizadas. Em métodos computacionais, a margem de erro é influenciada pela precisão da representação dos números e pelas limitações do hardware e software.
Modelo para Avaliação de Margem de Erro
Um modelo para avaliação da margem de erro pode incluir:
- Definição do nível de precisão desejado para o resultado final.
- Identificação das fontes potenciais de erro em cada etapa do cálculo.
- Estimação da margem de erro para cada fonte identificada.
- Combinação das margens de erro individuais para obter uma margem de erro total.
- Consideração do erro nas medidas iniciais dos lados do retângulo.
Utilizando este modelo, podemos ter uma estimativa da margem de erro em diferentes métodos e garantir resultados mais confiáveis em aplicações práticas. O modelo deve ser adaptado a cada caso específico, considerando as características dos cálculos e as necessidades de precisão da aplicação.
Fatores de Escalonamento e Proporção
Compreender como o comprimento e a largura de um retângulo afetam o comprimento da sua diagonal é crucial para aplicações práticas, desde o desenho técnico até a engenharia. Neste tópico, exploraremos a relação entre as dimensões do retângulo e o seu valor diagonal, destacando a influência da proporção entre comprimento e largura.A relação entre as dimensões do retângulo e a diagonal é fundamental.
Alterações em um ou ambos os valores afetam diretamente o comprimento da diagonal, e a proporção entre as dimensões influencia significativamente o resultado final. Analisaremos como estas variações ocorrem e demonstraremos exemplos concretos para facilitar a compreensão.
Influência do Escalonamento nas Dimensões
A alteração de uma ou ambas as dimensões de um retângulo resulta em uma mudança proporcional na diagonal. Se o comprimento e a largura forem aumentados ou diminuídos em uma determinada proporção, a diagonal também será afetada na mesma proporção. Isso demonstra a interdependência entre as dimensões e a diagonal.
Variações da Diagonal em Função das Dimensões
A diagonal de um retângulo é calculada através do Teorema de Pitágoras. A fórmula √(comprimento² + largura²) demonstra a relação entre as dimensões e a diagonal. Observe que qualquer alteração no comprimento ou largura impactará diretamente o valor da diagonal. Por exemplo, dobrar o comprimento de um retângulo duplicará a diagonal em relação ao retângulo original, mantendo a mesma proporção.
Analogamente, ao dobrar a largura, a diagonal também será duplicada, mantendo a proporção.
Exemplos Práticos de Escalonamento e Proporção
Considere um retângulo com comprimento de 3 cm e largura de 4 cm. A sua diagonal será √(3² + 4²) = 5 cm. Se o comprimento for duplicado para 6 cm, mantendo a largura em 4 cm, a nova diagonal será √(6² + 4²) = √52 ≈ 7,21 cm. Observe que o aumento do comprimento resultou em um aumento proporcional da diagonal.
Analogamente, se a largura for duplicada para 8 cm, a nova diagonal será √(3² + 8²) = √73 ≈ 8,54 cm.
Análise da Proporção entre as Dimensões
A proporção entre o comprimento e a largura do retângulo desempenha um papel fundamental na determinação do valor da diagonal. Um retângulo com comprimento e largura iguais (um quadrado) terá uma diagonal que se relaciona com as dimensões de forma mais direta. Retângulos com proporções diferentes (por exemplo, um retângulo muito mais comprido que largo) terão diagonais mais afetadas por mudanças no comprimento do que em mudanças na largura.
Essa análise da proporção entre as dimensões permite prever o impacto de mudanças em cada dimensão sobre o valor da diagonal.
Utilização de Ferramentas e Tecnologias: Dicas E Truques Para Calcular A Diagonal De Um Retângulo De Forma Eficiente.
A utilização de softwares e aplicativos pode simplificar e acelerar o cálculo da diagonal de um retângulo, especialmente em situações que envolvem cálculos repetitivos ou quando se precisa de alta precisão. Diversas ferramentas, desde calculadoras científicas até aplicativos online, oferecem recursos para esse tipo de cálculo, eliminando a necessidade de cálculos manuais e minimizando a possibilidade de erros.As ferramentas tecnológicas disponibilizam métodos rápidos e eficientes para determinar a diagonal, tornando o processo mais prático e acessível.
A precisão dos resultados também é aprimorada, reduzindo a margem de erros inerente aos cálculos feitos manualmente.
Calculadoras Científicas
As calculadoras científicas, comumente encontradas em lojas de informática ou em versões online, oferecem funcionalidades para o cálculo de raízes quadradas e, consequentemente, para a aplicação do Teorema de Pitágoras. Estas calculadoras facilitam a obtenção de resultados com grande precisão e agilidade. O uso de calculadoras científicas pode ser particularmente útil em contextos onde é necessária a repetição de cálculos, como em projetos de engenharia ou arquitetura.
Calculadoras Online
A internet disponibiliza diversas calculadoras online dedicadas a cálculos geométricos, incluindo o cálculo da diagonal de um retângulo. Essas ferramentas são acessíveis gratuitamente e em diversos idiomas, facilitando o acesso a estudantes e profissionais.
Passo a Passo para Uso de Ferramentas Online
Para utilizar calculadoras online, geralmente é suficiente fornecer as medidas dos lados do retângulo. Seguindo os passos abaixo, é possível calcular a diagonal com precisão:
- Acesse um site com uma calculadora online para cálculo de diagonais de retângulos.
- Insira os valores correspondentes aos lados do retângulo nas caixas de entrada.
- Clique no botão “calcular” ou “calcular diagonal”.
- O resultado, com a diagonal do retângulo, será exibido na tela.
Comparação de Precisão e Velocidade
A precisão e a velocidade dos cálculos variam entre as diferentes ferramentas. Calculadoras científicas, em geral, oferecem alta precisão, mas podem exigir o conhecimento prévio de como utilizar suas funções. Calculadoras online são convenientes e rápidas, geralmente fornecendo resultados em segundos. A escolha da ferramenta dependerá do contexto específico e das necessidades do usuário.
Dicas e Truques para Cálculo Eficiente
Ao calcular a diagonal de um retângulo, a escolha do método mais eficiente pode significar ganho de tempo e precisão. Compreender as diferentes abordagens e as potenciais armadilhas nos cálculos é fundamental para obter resultados confiáveis e otimizar o processo. Este tópico apresenta dicas e truques para tornar o cálculo da diagonal de um retângulo mais eficaz.A eficiência no cálculo da diagonal de um retângulo está intrinsecamente ligada à escolha do método mais apropriado, levando em consideração as características dos dados e a necessidade de precisão.
Identificar atalhos e evitar erros comuns são essenciais para obter resultados corretos e economizar tempo.
Comparação de Métodos de Cálculo, Dicas e truques para calcular a diagonal de um retângulo de forma eficiente.
Os métodos para calcular a diagonal de um retângulo podem variar em complexidade e eficiência. O Teorema de Pitágoras é o método mais comum e geralmente o mais eficiente. Outros métodos, como o uso de proporções ou a utilização de fórmulas específicas para determinados tipos de retângulos, podem ser mais adequados em situações específicas.
- O Teorema de Pitágoras, baseado no relacionamento entre os lados e a diagonal, é a abordagem mais generalizada e frequentemente a mais eficiente. A sua aplicação é ampla, abrangendo diversos tipos de retângulos. Para calcular a diagonal, utilizamos a seguinte fórmula:
d = √(a² + b²)
onde d representa a diagonal, a e b representam os lados do retângulo.
- Para retângulos especiais, como quadrados, onde os lados são iguais ( a = b), a fórmula simplifica para:
d = a√2
Esta simplificação proporciona um cálculo mais rápido e direto.
- Métodos baseados em proporções podem ser aplicados quando se conhece a relação entre os lados do retângulo e a diagonal. Essa abordagem, embora útil em certas situações, não é tão amplamente aplicável como o Teorema de Pitágoras.
Identificação de Atalhos e Técnicas de Otimização
A identificação de atalhos e técnicas para otimizar o processo de cálculo é crucial para maximizar a eficiência.
- Utilizar calculadoras ou softwares apropriados pode acelerar o processo de cálculo, especialmente em casos com números complexos ou cálculos repetitivos. A precisão dos resultados deve ser verificada, independentemente da ferramenta utilizada.
- Utilizar fórmulas simplificadas quando possível, como a fórmula para a diagonal de um quadrado, permite um cálculo mais rápido e eficiente. Essa simplificação reduz o número de etapas e minimiza potenciais erros.
- Desenvolver o hábito de estimar os resultados antes de calcular, permitindo identificar possíveis desvios ou erros de cálculo. Essa prática pode ajudar a verificar a plausibilidade dos resultados obtidos.
Dicas para Evitar Erros Comuns
A atenção aos detalhes e a verificação dos cálculos são essenciais para evitar erros comuns.
- Verificar cuidadosamente as unidades de medida dos lados do retângulo para garantir a consistência nas operações e a correção do resultado final.
- Reduzir a chance de erros ao registrar os dados corretamente antes de iniciar o cálculo.
- Utilizar a verificação cruzada de cálculos, seja por meio de um método alternativo ou da verificação manual, para minimizar potenciais erros.
Guia Passo a Passo para Cálculo Eficiente
Um guia passo a passo facilita a aplicação dos conceitos.
- Identifique as medidas dos lados do retângulo.
- Escolha o método mais adequado para o cálculo da diagonal (Teorema de Pitágoras ou fórmula simplificada para quadrados).
- Substitua os valores das medidas dos lados na fórmula escolhida.
- Realize os cálculos e obtenha o resultado da diagonal.
- Verifique a plausibilidade do resultado e as unidades de medida.
Ilustrações e Visualizações
A visualização é crucial para a compreensão de conceitos abstratos, como o cálculo da diagonal de um retângulo. Imagens e diagramas tornam o processo mais intuitivo, permitindo a assimilação rápida das relações geométricas envolvidas. Através de representações visuais, é possível identificar padrões e conexões entre os elementos, facilitando a aplicação do Teorema de Pitágoras e outros métodos alternativos.Ilustrações claras e bem elaboradas, com anotações precisas, ajudam a consolidar o entendimento, promovendo a retenção de informações e a aplicação prática dos conceitos.
As representações visuais podem ser adaptadas a diferentes níveis de complexidade, desde exemplos simples até situações mais elaboradas, tornando o aprendizado mais acessível e eficaz.
Representação do Teorema de Pitágoras em um Retângulo
Para ilustrar o Teorema de Pitágoras no contexto de um retângulo, imagine um retângulo ABCD. Desenhe os lados do retângulo, representando-os como segmentos de reta com comprimentos específicos (por exemplo, AB = 3 cm e BC = 4 cm). Em seguida, trace a diagonal AC, que representa a hipotenusa do triângulo retângulo formado pelos lados do retângulo. Anotações importantes devem ser incluídas para indicar que os ângulos formados pelos lados do retângulo são retos (90°).
Isso demonstra visualmente a relação entre os lados e a diagonal. O triângulo retângulo formado pela diagonal e os lados permite aplicar o Teorema de Pitágoras, como segue:
a² + b² = c²
onde ‘a’ e ‘b’ são os comprimentos dos lados e ‘c’ é o comprimento da diagonal.
Diagramas e Análises
Para melhor compreensão, é fundamental criar diagramas detalhados que mostrem a aplicação prática do Teorema de Pitágoras. Um diagrama pode ilustrar um retângulo com dimensões específicas, por exemplo, 5 cm de largura e 12 cm de comprimento. A diagonal é traçada, e os valores de cada lado são rotulados no diagrama. O quadrado dos lados (5² e 12²) é calculado separadamente, e a soma desses quadrados é comparada ao quadrado da diagonal (c²).
Este exemplo prático demonstra como o Teorema de Pitágoras relaciona os lados e a diagonal do retângulo. O diagrama deve ser acompanhado de anotações que expliquem cada etapa do cálculo.
Importância das Visualizações
As visualizações, através de diagramas e ilustrações, desempenham um papel fundamental na compreensão do cálculo da diagonal de um retângulo. Elas tornam o conceito mais tangível, permitindo a visualização das relações geométricas envolvidas. A representação gráfica ajuda a identificar padrões, a entender a lógica por trás do Teorema de Pitágoras e a aplicar o conhecimento em diferentes contextos.
Através de exemplos práticos, as visualizações demonstram a aplicabilidade do conceito em situações do mundo real. As visualizações facilitam a compreensão dos conceitos e a aplicação prática, o que é essencial para a aprendizagem eficaz.
Em resumo, este guia forneceu uma visão abrangente sobre o cálculo da diagonal de um retângulo, desde os conceitos básicos até métodos avançados e a utilização de ferramentas. Esperamos que você tenha compreendido os diferentes métodos e suas aplicações práticas, otimizando seus cálculos e evitando erros comuns. A combinação de conhecimento teórico e prático, aliada a dicas para o cálculo eficiente, o tornará mais confiante e preciso em suas próximas medições.
Qual a importância do cálculo da diagonal de um retângulo?
O cálculo da diagonal é fundamental em diversas áreas, como arquitetura, engenharia, carpintaria e design, permitindo a determinação de comprimentos e ângulos em projetos e construções.
Quais as fórmulas para calcular a diagonal de um retângulo?
A fórmula mais comum é a baseada no Teorema de Pitágoras: diagonal² = comprimento² + largura².
Como evitar erros comuns no cálculo da diagonal?
Atenção aos sinais ao elevar ao quadrado e à correta aplicação da raiz quadrada. Verificar se as unidades de medida estão consistentes.
Existe algum software que auxilie no cálculo da diagonal de um retângulo?
Sim, existem calculadoras científicas, softwares de desenho vetorial e planilhas eletrônicas que facilitam o cálculo da diagonal, garantindo maior precisão e rapidez.