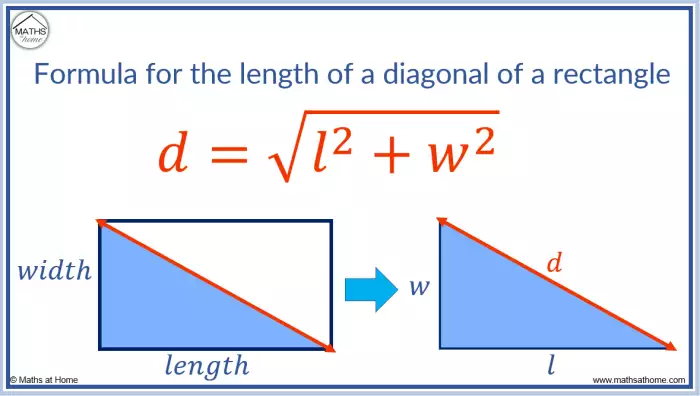
A Fórmula da diagonal de um retângulo em termos de comprimento e largura. descreve a relação entre as dimensões de um retângulo e o comprimento de sua diagonal. Compreender essa fórmula é fundamental para resolver problemas geométricos, permitindo calcular a diagonal de um retângulo conhecendo apenas seu comprimento e largura. Esta fórmula, derivada do Teorema de Pitágoras, encontra aplicações práticas em diversas áreas, desde o cálculo da diagonal de uma tela de computador até a medição de objetos retangulares em projetos de engenharia e arquitetura.
A fórmula da diagonal de um retângulo é uma ferramenta poderosa que permite determinar o comprimento da diagonal conhecendo o comprimento e a largura do retângulo. Ela surge como uma consequência direta do Teorema de Pitágoras, relacionando esses três elementos de forma precisa e eficiente. O uso prático desta fórmula vai desde a medição de objetos até a resolução de problemas mais complexos, demonstrando sua importância no campo da geometria.
Introdução à Fórmula da Diagonal de um Retângulo
A diagonal de um retângulo é um segmento de reta que une dois vértices opostos do retângulo. Compreender a relação entre a diagonal, o comprimento e a largura do retângulo é fundamental para diversas aplicações em geometria e em áreas como engenharia e arquitetura. Esta fórmula permite calcular a medida da diagonal conhecendo as dimensões do retângulo, simplificando cálculos e resolvendo problemas de forma eficiente.A fórmula da diagonal de um retângulo baseia-se no Teorema de Pitágoras.
Geometricamente, a diagonal forma um triângulo retângulo com os lados do retângulo, onde a diagonal é a hipotenusa e os lados são os catetos. Este triângulo retângulo permite aplicar diretamente o Teorema de Pitágoras para determinar o comprimento da diagonal.
Definição da Fórmula
A fórmula da diagonal de um retângulo relaciona a diagonal (d) ao comprimento (l) e à largura (w) do retângulo. A fórmula é expressa como:
d = √(l² + w²)
onde:
- d representa o comprimento da diagonal;
- l representa o comprimento do retângulo;
- w representa a largura do retângulo.
Relação Geométrica entre Lados e Diagonal
A relação entre os lados e a diagonal de um retângulo é fundamental para entender a fórmula. A diagonal é a hipotenusa de um triângulo retângulo cujos catetos correspondem ao comprimento e à largura do retângulo. A aplicação do Teorema de Pitágoras, neste contexto, demonstra que o quadrado da diagonal é igual à soma dos quadrados do comprimento e da largura.
Importância da Fórmula
A fórmula da diagonal é crucial para a resolução de problemas geométricos que envolvem retângulos. Por exemplo, ao projetar estruturas, calcular áreas de terrenos ou analisar a capacidade de armazenamento em caixas retangulares, o conhecimento desta fórmula é essencial. Em cada caso, a fórmula permite determinar a medida da diagonal, que pode ser fundamental para a resolução do problema em questão.
Elementos Fundamentais da Fórmula
A tabela a seguir apresenta os elementos fundamentais da fórmula da diagonal de um retângulo, juntamente com suas descrições:
| Nome do Elemento | Descrição |
|---|---|
| d | Comprimento da diagonal do retângulo. |
| l | Comprimento do retângulo. |
| w | Largura do retângulo. |
Demonstração da Fórmula
Para determinar a medida da diagonal de um retângulo, podemos recorrer ao Teorema de Pitágoras. Este teorema estabelece uma relação fundamental entre os lados de um triângulo retângulo, permitindo calcular a medida de um lado desconhecido a partir das medidas dos outros dois. Aplicando o Teorema de Pitágoras a um retângulo, podemos deduzir a fórmula para a diagonal.
Demonstração Utilizando o Teorema de Pitágoras
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). Em um retângulo, podemos visualizar um triângulo retângulo utilizando a diagonal como hipotenusa e dois lados adjacentes como catetos.
| Etapa | Cálculo | Explicação |
|---|---|---|
| 1 | Considerando um retângulo com comprimento (l) e largura (w), a diagonal (d) forma um triângulo retângulo com os lados l e w. | Estabelecendo o contexto geométrico para a aplicação do Teorema de Pitágoras. |
| 2 | Aplicando o Teorema de Pitágoras: d² = l² + w² | A fórmula do Teorema de Pitágoras relaciona a hipotenusa (diagonal) ao quadrado dos catetos (comprimento e largura). |
| 3 | Isolando a variável d: d = √(l² + w²) | Para obter a medida da diagonal, calcula-se a raiz quadrada da soma dos quadrados do comprimento e da largura. |
A fórmula resultante, d = √(l² + w²), fornece a medida da diagonal de um retângulo em função do seu comprimento e largura.
Aplicações Práticas
A fórmula da diagonal de um retângulo encontra diversas aplicações em situações do dia a dia, indo desde cálculos simples até projetos mais complexos. Compreender como utilizá-la permite solucionar problemas práticos envolvendo formas retangulares.
Exemplos de Problemas
A fórmula da diagonal é fundamental para determinar o comprimento da diagonal em diversos objetos retangulares. A seguir, são apresentados exemplos que demonstram a aplicação prática da fórmula.
- Cálculo da diagonal de uma tela de computador: Imagine um monitor de 24 polegadas de largura e 18 polegadas de altura. Qual é o comprimento da diagonal da tela? Essa informação é útil para saber o tamanho real do monitor, um fator importante na experiência do usuário.
- Cálculo da diagonal de uma folha de papel: Uma folha de papel A4 possui dimensões de 21 cm de largura e 29,7 cm de comprimento. Qual é a diagonal dessa folha? O conhecimento da diagonal é útil para determinar o espaço necessário para armazenar ou manipular a folha.
- Cálculo da diagonal de um quadro: Um quadro tem 50 cm de largura e 70 cm de comprimento. Qual é o comprimento da diagonal? Essa informação é relevante para o enquadramento da obra de arte, o transporte e a organização do quadro na parede.
Cálculo Passo a Passo
A aplicação do Teorema de Pitágoras é fundamental para calcular a diagonal de um retângulo. Este teorema estabelece uma relação entre os lados de um triângulo retângulo, onde o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). No caso do retângulo, a diagonal representa a hipotenusa, e os lados do retângulo são os catetos.
- Exemplo 1: Considerando um retângulo com comprimento de 5 cm e largura de 12 cm.
1. Identificar as variáveis
comprimento = 5 cm, largura = 12 cm.
2. Aplicar o Teorema de Pitágoras
diagonal² = comprimento² + largura².
3. Substituir os valores
diagonal² = 5² + 12².
4. Calcular os quadrados
diagonal² = 25 +
-
5. Somar os quadrados
diagonal² =
6. Calcular a raiz quadrada
diagonal = √169 = 13 cm.
-
- Exemplo 2: Um retângulo com comprimento de 8 cm e largura de 6 cm.
1. Identificar as variáveis
comprimento = 8 cm, largura = 6 cm.
2. Aplicar o Teorema de Pitágoras
diagonal² = comprimento² + largura².
3. Substituir os valores
diagonal² = 8² + 6².
4. Calcular os quadrados
diagonal² = 64 +
-
5. Somar os quadrados
diagonal² =
6. Calcular a raiz quadrada
diagonal = √100 = 10 cm.
-
- Exemplo 3: Um retângulo com comprimento de 10 m e largura de 15 m.
1. Identificar as variáveis
comprimento = 10 m, largura = 15 m.
2. Aplicar o Teorema de Pitágoras
diagonal² = comprimento² + largura².
3. Substituir os valores
diagonal² = 10² + 15².
4. Calcular os quadrados
diagonal² = 100 +
-
5. Somar os quadrados
diagonal² =
6. Calcular a raiz quadrada
diagonal = √325 ≈ 18,03 m.
-
Tabela de Exemplos
A tabela a seguir apresenta diversos exemplos de cálculos de diagonais de retângulos, com suas respectivas interpretações.
| Comprimento | Largura | Diagonal Calculada | Interpretação do Resultado |
|---|---|---|---|
| 3 cm | 4 cm | 5 cm | A diagonal é a hipotenusa do triângulo retângulo formado pelos lados do retângulo. |
| 6 cm | 8 cm | 10 cm | A diagonal é maior que os lados do retângulo. |
| 10 cm | 15 cm | 18,03 cm | A diagonal é maior que os lados do retângulo. |
| 24 pol | 18 pol | 29,99 pol | Diagonal de um monitor de computador. |
| 21 cm | 29,7 cm | 35,65 cm | Diagonal de uma folha de papel A4. |
| 50 cm | 70 cm | 86,02 cm | Diagonal de um quadro. |
Aplicações em Situações do Mundo Real
A fórmula da diagonal é fundamental para diversas aplicações práticas. Considere os seguintes exemplos:
- Tela de computador (24 pol largura, 18 pol altura): A diagonal calculada (aproximadamente 29,99 polegadas) indica o tamanho real da tela, influenciando na experiência visual do usuário. Uma tela maior proporciona uma visão mais ampla e detalhada.
- Folha de papel A4 (21 cm largura, 29,7 cm comprimento): A diagonal (aproximadamente 35,65 cm) é útil para o armazenamento e manuseio da folha. Conhecendo a diagonal, é possível otimizar o espaço necessário para arquivamento ou transporte.
- Quadro (50 cm largura, 70 cm comprimento): A diagonal (aproximadamente 86,02 cm) é relevante para a composição da obra de arte e a percepção visual da mesma. O tamanho da diagonal afeta a maneira como a obra é vista e apreciada.
Comparação com outras figuras geométricas
A comparação entre as fórmulas das diagonais de retângulos e quadrados permite compreender melhor as relações entre as propriedades geométricas e as expressões matemáticas. Analisando as diferenças e semelhanças, podemos extrair conclusões importantes sobre a generalização dessas fórmulas para outros quadriláteros.
Comparação das fórmulas para retângulos e quadrados
Para determinar a diagonal de um retângulo ou de um quadrado, utilizamos o Teorema de Pitágoras. A demonstração para cada figura é apresentada a seguir.
Demonstração para o retângulo
Considere um retângulo com lados de comprimento `a` e largura `b`. A diagonal `d` divide o retângulo em dois triângulos retângulos congruentes, com catetos `a` e `b`. Aplicando o Teorema de Pitágoras, temos:
`d² = a² + b²`
`d = √(a² + b²) `
 Figura: Retângulo com diagonal. O retângulo é representado com lados a e b, e a diagonal é representada por d.
Figura: Retângulo com diagonal. O retângulo é representado com lados a e b, e a diagonal é representada por d.
Demonstração para o quadrado
Considere um quadrado com lado de comprimento `a`. A diagonal `d` divide o quadrado em dois triângulos retângulos isósceles congruentes, com catetos `a` e `a`. Aplicando o Teorema de Pitágoras, temos:
`d² = a² + a²`
`d² = 2a²`
`d = √(2a²) = a√2`
 Figura: Quadrado com diagonal. O quadrado é representado com lado a, e a diagonal é representada por d.
Figura: Quadrado com diagonal. O quadrado é representado com lado a, e a diagonal é representada por d.
Diferenças e semelhanças
As fórmulas demonstram que, enquanto a diagonal de um retângulo depende dos comprimentos de ambos os lados (`a` e `b`), a diagonal de um quadrado depende apenas do comprimento de um dos seus lados (`a`). Ambas as fórmulas são derivadas do Teorema de Pitágoras, o que demonstra a relação fundamental entre os lados e a diagonal de uma figura geométrica.
Tabela comparativa
A tabela a seguir resume as fórmulas e propriedades relevantes para as diagonais de retângulos e quadrados.
| Figura | Fórmula (LaTeX) | Propriedades |
|---|---|---|
 Retângulo Retângulo |
`d = √(a² + b²) ` | Lados opostos paralelos e congruentes, ângulos internos retos. |
 Quadrado Quadrado |
`d = a√2` | Lados congruentes, ângulos internos retos. |
Generalização para outros quadriláteros
A fórmula da diagonal não pode ser generalizada para todos os quadriláteros. Para derivar uma fórmula específica para um quadrilátero, é necessário conhecer as propriedades específicas desse quadrilátero, como a congruência dos lados, a paralelismo dos lados opostos, e as medidas dos ângulos. A fórmula da diagonal pode ser derivada para paralelogramos, trapézios isósceles e outros quadriláteros específicos, utilizando o Teorema de Pitágoras ou outras ferramentas geométricas.
Diferenças e semelhanças entre as diagonais
As diagonais de retângulos e quadrados, apesar de derivadas da mesma premissa (Teorema de Pitágoras), possuem características distintas. Retângulos, com lados opostos paralelos e congruentes, têm diagonais com comprimentos calculados pela soma dos quadrados dos lados, ao passo que quadrados, com lados congruentes, têm diagonais com comprimentos calculados pela multiplicação do lado por raiz quadrada de 2. A geometria desempenha um papel crucial na engenharia, arquitetura e outras áreas, fornecendo ferramentas para cálculos precisos, como os relacionados à determinação de diagonais.
Por exemplo, em arquitetura, o conhecimento das diagonais de um retângulo ou quadrado é fundamental para o cálculo de áreas e perímetros de superfícies. Em engenharia, a precisão em cálculos de diagonais é essencial para a construção de estruturas estáveis e eficientes.
Interpretação Geométrica
A compreensão da fórmula da diagonal de um retângulo ganha uma nova dimensão quando analisada sob a ótica da geometria analítica. Esta abordagem permite visualizar o retângulo em um sistema de coordenadas cartesianas, facilitando a demonstração e a aplicação da fórmula. A relação entre a diagonal e a distância entre dois pontos torna-se evidente, fornecendo uma interpretação mais profunda do conceito.
Representação dos Pontos em um Sistema de Coordenadas
Para aplicar a geometria analítica, representamos os vértices do retângulo em um sistema de coordenadas cartesianas. Suponha um retângulo com comprimento ‘l’ e largura ‘w’. Podemos posicioná-lo no plano cartesiano de forma que dois vértices estejam sobre o eixo x e dois sobre o eixo y. Por exemplo, os vértices podem ser (0, 0), (l, 0), (l, w) e (0, w).
Esta representação permite utilizar as ferramentas da geometria analítica para calcular a diagonal.
Fórmula da Distância entre Dois Pontos
A fórmula da distância entre dois pontos no plano cartesiano é fundamental para o cálculo da diagonal de um retângulo. Dado dois pontos A(x 1, y 1) e B(x 2, y 2), a distância entre eles é calculada pela fórmula:
d = √((x2
- x 1) 2 + (y 2
- y 1) 2)
Esta fórmula é derivada do Teorema de Pitágoras e representa a hipotenusa de um triângulo retângulo cujos catetos são as diferenças nas coordenadas x e y dos dois pontos.
Relação entre a Fórmula da Diagonal e a Distância entre Dois Pontos
A fórmula da diagonal de um retângulo é uma aplicação direta da fórmula da distância entre dois pontos. Considerando dois vértices opostos do retângulo, como (0, 0) e (l, w), podemos aplicar a fórmula da distância para calcular o comprimento da diagonal. Substituindo as coordenadas dos pontos na fórmula, obtemos:
d = √((l – 0)2 + (w – 0) 2) = √(l 2 + w 2)
Esta expressão coincide com a fórmula da diagonal que conhecemos, demonstrando a relação intrínseca entre os conceitos. A diagonal do retângulo representa a distância entre dois vértices opostos, calculada através da fórmula da distância entre dois pontos.
Problemas de Encontro e Aplicação
A fórmula da diagonal de um retângulo permite calcular a distância mais curta entre dois pontos opostos do retângulo. Esta aplicação se estende para problemas mais complexos, envolvendo encontros e trajetórias, onde a diagonal representa o caminho mais eficiente em um espaço retangular. Compreender a aplicação da fórmula em cenários práticos, desde encontrar a distância entre dois pontos até situações com obstáculos, é crucial para diversas áreas, como engenharia, arquitetura e até mesmo jogos.
Aplicações em Problemas de Encontro
A fórmula da diagonal pode ser aplicada para resolver problemas de encontro em retângulos, considerando diferentes tipos de encontros. Um encontro em um ponto específico do retângulo envolve calcular a distância diagonal para chegar a esse ponto. Já um encontro em um segmento de reta, dentro do retângulo, envolve a utilização da fórmula para determinar o ponto de encontro, considerando as coordenadas dos pontos iniciais e finais.
Distância entre Dois Pontos em Retângulos
A fórmula da diagonal é fundamental para calcular a distância mais curta entre dois pontos em um retângulo, seja ele horizontal, vertical ou inclinado. Considerando diferentes orientações do retângulo, a aplicação do Teorema de Pitágoras permite encontrar a distância diagonal, que representa o caminho mais curto entre os pontos.
Considerando Obstáculos
A fórmula da diagonal pode ser adaptada para situações com obstáculos dentro do retângulo. Para encontrar o caminho mais curto entre dois pontos, levando em conta a presença de obstáculos retangulares ou outros objetos, é necessário calcular a distância diagonal do retângulo original e comparar com o trajeto que passa pelos obstáculos. Neste caso, a otimização do caminho é essencial.
Exemplos de Aplicações
| Descrição do Problema | Etapas de Resolução | Resultado |
|---|---|---|
| Encontrar a distância entre dois pontos opostos de um retângulo horizontal. | 1. Identificar as coordenadas dos pontos. 2. Calcular a distância entre as coordenadas x e a distância entre as coordenadas y. 3. Utilizar o teorema de Pitágoras (diagonal² = lado x² + lado y²) para encontrar a distância da diagonal. | Valor numérico da distância. Por exemplo, se os pontos forem (0,0) e (3,4), a distância será 5. |
| Encontrar a distância entre dois pontos em um retângulo vertical, considerando um obstáculo retangular. | 1. Desenhar o retângulo e o obstáculo. 2. Calcular a distância entre os pontos considerando o caminho mais curto, que pode envolver passar pelo obstáculo. 3. Calcular a distância diagonal do retângulo, considerando a distância livre de obstáculos, caso exista um caminho mais curto. | Valor numérico da distância, considerando o caminho mais curto. Por exemplo, se o obstáculo bloquear parte do caminho, o resultado será a distância diagonal diminuída da distância ocupada pelo obstáculo. |
| Encontrar a distância entre dois pontos em um retângulo inclinado. | 1. Calcular as coordenadas dos pontos e a inclinação do retângulo. 2. Utilizar o teorema de Pitágoras para encontrar a distância na diagonal. 3. Descrever o método usado para encontrar a distância, considerando a inclinação do retângulo. É necessário projetar os pontos em um plano cartesiano para calcular a distância na diagonal. | Valor numérico da distância, incluindo a inclinação. |
| Encontrar a distância entre dois pontos em um retângulo, onde um ponto está fora do retângulo. | 1. Desenhar o retângulo e os pontos. 2. Calcular a distância entre o ponto externo e o ponto mais próximo no retângulo. 3. Utilizar o teorema de Pitágoras para encontrar a distância total, considerando o caminho mais curto, que pode envolver sair do retângulo para alcançar o ponto. | Valor numérico da distância, incluindo o caminho fora do retângulo. |
Código Python para Cálculo de Distância
“`pythonimport mathdef distancia_diagonal(x1, y1, x2, y2): “””Calcula a distância entre dois pontos em um retângulo.””” distancia = math.sqrt((x2 – x1) 2 + (y2 – y1)2) return distancia#Exemplo de uso:ponto1 = (0, 0)ponto2 = (3, 4)distancia = distancia_diagonal(ponto1[0], ponto1[1], ponto2[0], ponto2[1])print(f”A distância entre os pontos é: distancia”)“`Este código Python calcula a distância entre dois pontos, utilizando a fórmula da diagonal. É importante adaptar o código para lidar com situações mais complexas, como a presença de obstáculos.
Limitações da Fórmula
A fórmula da diagonal de um retângulo assume um espaço plano e sem obstáculos. Em situações com superfícies curvas, relevos ou dimensões não retangulares, a aplicação da fórmula pode ser imprecisa ou inapropriada. Além disso, a presença de obstáculos complexos pode dificultar a determinação do caminho mais curto.
Exemplos de Problemas
Para consolidar o aprendizado da fórmula da diagonal de um retângulo, apresentamos a seguir cinco problemas práticos. Cada um deles envolve diferentes contextos e solicitações, permitindo a aplicação da fórmula em situações do cotidiano.
Problemas de Aplicação da Fórmula
Os exemplos a seguir ilustram a aplicação da fórmula da diagonal de um retângulo em situações diversas. Cada problema fornece as dimensões do retângulo e requer o cálculo do comprimento da diagonal.
| Enunciado | Solução | Resposta |
|---|---|---|
| Uma sala retangular tem 3 metros de largura e 4 metros de comprimento. Qual o comprimento da diagonal da sala? | Aplicando a fórmula da diagonal de um retângulo, D = √(l² + w²), onde ‘l’ é o comprimento e ‘w’ é a largura. Neste caso, l = 4 metros e w = 3 metros. D = √(4² + 3²) = √(16 + 9) = √25 = 5 metros. | 5 metros |
| Um terreno retangular possui 12 metros de comprimento e 5 metros de largura. Qual o comprimento da diagonal do terreno? | Utilizando a fórmula D = √(l² + w²), com l = 12 metros e w = 5 metros. D = √(12² + 5²) = √(144 + 25) = √169 = 13 metros. | 13 metros |
| Um painel retangular de publicidade tem 8 metros de largura e a sua diagonal mede 10 metros. Qual o comprimento do painel? | Usando a fórmula D = √(l² + w²), temos D = 10 metros e w = 8 metros. 10² = l² + 8² 100 = l² + 64 l² = 36 l = 6 metros. | 6 metros |
| Uma porta retangular tem 2,5 metros de largura e 2 metros de altura. Qual o comprimento da diagonal da porta? | Aplicando a fórmula D = √(l² + w²), onde l = 2 metros e w = 2,5 metros. D = √(2² + 2,5²) = √(4 + 6,25) = √10,25 ≈ 3,20 metros. | Aproximadamente 3,20 metros |
| Um jardim retangular tem 6,4 metros de comprimento e 4,8 metros de largura. Calcule o comprimento da diagonal do jardim. | Aplicando a fórmula D = √(l² + w²), onde l = 6,4 metros e w = 4,8 metros. D = √(6,4² + 4,8²) = √(40,96 + 23,04) = √64 = 8 metros. | 8 metros |
Considerações Adicionais
A fórmula da diagonal de um retângulo, derivada do Teorema de Pitágoras, fornece uma relação fundamental entre o comprimento, a largura e a diagonal do retângulo. Entretanto, como qualquer fórmula matemática, ela possui limitações e condições específicas para sua aplicação. Analisaremos esses aspectos com precisão, garantindo a compreensão adequada de sua utilização prática.
Limitações da Fórmula
A fórmula da diagonal de um retângulo baseia-se em relações geométricas e não se aplica a todas as situações. É crucial compreender suas restrições para garantir o uso correto da fórmula.
- A fórmula presume que o objeto seja um retângulo. Se o objeto for um paralelogramo não-retângulo, a fórmula não será aplicável. Por exemplo, um losango, apesar de possuir lados iguais, não tem seus lados perpendiculares, assim a fórmula para a diagonal de um retângulo não é válida.
- A fórmula requer que as dimensões (comprimento e largura) sejam valores positivos. Valores negativos ou nulos não fazem sentido no contexto de medidas de comprimento e largura. Por exemplo, um comprimento de -5 cm não representa uma medida física válida.
- A fórmula pressupõe que o retângulo esteja no plano cartesiano. Se o retângulo for inclinado ou estiver em um espaço tridimensional, a fórmula necessita de adaptações.
Condições de Validade, Fórmula da diagonal de um retângulo em termos de comprimento e largura.
Para que a fórmula da diagonal seja válida, certas condições devem ser respeitadas. A aplicação da fórmula depende de sua conformidade com esses requisitos.
- As dimensões do retângulo (comprimento e largura) devem ser números reais positivos. A fórmula não se aplica a figuras com dimensões negativas ou nulas.
- A relação entre comprimento e largura deve ser a de um retângulo. Em outras palavras, os lados devem ser perpendiculares entre si. Isso é crucial para a aplicação do Teorema de Pitágoras, a base da fórmula.
Tabela de Limitações e Condições
| Condição | Explicação |
|---|---|
| Dimensões Positivas | A fórmula só é válida se o comprimento e a largura do retângulo forem números reais positivos. Exemplos de aplicação: retângulos com dimensões 5 cm e 10 cm; 2 m e 3 m. Exemplos de não-aplicação: retângulos com dimensões -3 cm e 4 cm; 0 m e 2 m. |
| Ângulos Retos | A fórmula pressupõe ângulos retos entre os lados do retângulo. Exemplos de aplicação: retângulos padrão. Exemplos de não-aplicação: paralelogramos que não são retângulos. |
| Objeto Bidimensional | A fórmula se aplica a retângulos no plano cartesiano. Em casos de retângulos em espaços tridimensionais, a fórmula precisa de adaptações. Exemplos de aplicação: retângulos no papel, em um desenho. Exemplos de não-aplicação: retângulos em um modelo 3D. |
| Definição de Retângulo | A fórmula pressupõe que o objeto seja um retângulo. Exemplos de aplicação: figuras com lados perpendiculares e comprimento e largura definidos. Exemplos de não-aplicação: objetos que não se encaixam na definição geométrica de um retângulo. |
Esclarecimentos Adicionais
- Restrições Numéricas: A fórmula aceita valores decimais e fracionários para comprimento e largura. Valores inteiros são um caso específico dentro desse conjunto maior.
- Domínio das Variáveis: O domínio das variáveis comprimento e largura é o conjunto dos números reais positivos.
- Contexto: A fórmula da diagonal de um retângulo é fundamental em geometria plana e tem aplicações em diversas áreas, como arquitetura, engenharia e design.
Fórmulas Relacionadas: Fórmula Da Diagonal De Um Retângulo Em Termos De Comprimento E Largura.
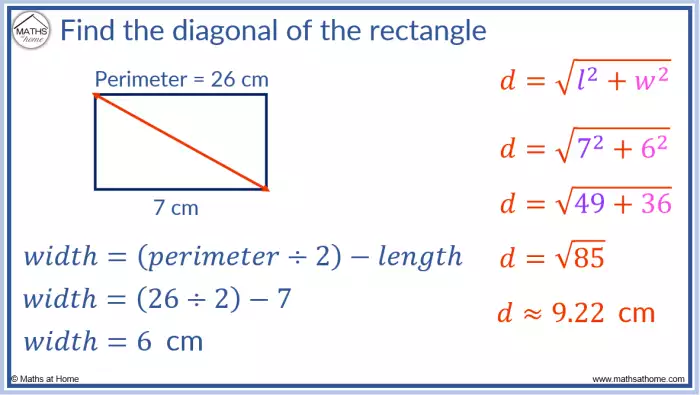
Além da fórmula da diagonal, outras fórmulas matemáticas são essenciais para o completo entendimento das propriedades dos retângulos. Compreender a relação entre o cálculo do perímetro, da área, e das propriedades dos ângulos com a diagonal permite uma análise mais profunda da geometria do retângulo. Nesta seção, serão apresentadas as fórmulas relacionadas ao retângulo, detalhando a influência da diagonal em cada uma delas.
Fórmulas Relacionadas ao Retângulo
Um retângulo é um quadrilátero com quatro ângulos retos. Suas propriedades geométricas permitem o cálculo de diversas medidas, como perímetro, área e diagonal. O Teorema de Pitágoras é fundamental para relacionar essas medidas.
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). No caso de um retângulo, a diagonal atua como a hipotenusa de um dos triângulos retângulos formados pelas suas arestas. A fórmula para calcular a diagonal (d) de um retângulo com comprimento (c) e largura (l) é: d 2 = c 2 + l 2.
| Fórmula | Descrição | Relação com a Diagonal |
|---|---|---|
Perímetro = 2
|
Soma dos lados do retângulo. | A diagonal não afeta diretamente o perímetro, mas o comprimento e a largura podem ser relacionados à diagonal usando o Teorema de Pitágoras. Por exemplo, se d = 10 cm, c = 6 cm, então l2 = 10 2
|
| Área = comprimento – largura | Área interna do retângulo. | A diagonal não afeta diretamente a área, mas o comprimento e a largura podem ser relacionados à diagonal usando o Teorema de Pitágoras. Por exemplo, se d = 10 cm, c = 8 cm, então l2 = 102
|
| Teorema de Pitágoras: diagonal2 = comprimento2 + largura2 | Relação entre a diagonal, comprimento e largura. | Essencial para relacionar as outras fórmulas com a diagonal. Se a diagonal for 10 cm, o comprimento e a largura podem variar, mas a relação sempre se manterá. Por exemplo, se c = 6 cm, então l2 = 102
|
| Ângulo entre a diagonal e o lado: arctg(largura/comprimento) | Cálculo do ângulo agudo formado pela diagonal e um lado. | A diagonal influencia diretamente nesse ângulo, pois o ângulo depende da relação entre a largura e o comprimento. Por exemplo, se d = 10 cm, e l = 6 cm, então c2 = 10 26 2 = 64, logo c = 8 cm. O ângulo será arctg(6/8) ≈ 36,87°. |
Exercícios Práticos
Para consolidar o aprendizado da fórmula da diagonal de um retângulo, apresentamos uma série de exercícios práticos. Estes problemas abrangem diferentes contextos e níveis de complexidade, permitindo que o aluno aplique a fórmula e desenvolva sua capacidade de resolução de problemas geométricos.
Problemas Envolvendo Cálculo da Diagonal
Nesta seção, serão apresentados problemas que exigem o cálculo da diagonal de um retângulo, dados o comprimento e a largura. É fundamental lembrar a fórmula da diagonal: d = √(l² + w²), onde d representa a diagonal, l o comprimento e w a largura.
- Um retângulo possui comprimento de 6 cm e largura de 8 cm. Qual o comprimento da diagonal?
- Um terreno retangular possui 12 metros de comprimento e 5 metros de largura. Qual o comprimento da diagonal do terreno?
- Uma sala retangular tem 10 pés de largura e 15 pés de comprimento. Determine o comprimento da diagonal da sala.
- Um retângulo possui diagonal medindo 17 cm e comprimento de 8 cm. Determine a largura do retângulo.
- Uma placa retangular possui diagonal de 25 cm e largura de 15 cm. Qual o comprimento da placa?
Problemas Envolvendo Aplicação em Contextos
Nesta seção, os problemas envolvem a aplicação da fórmula da diagonal em cenários do dia a dia, como encontrar a distância entre dois pontos opostos de um terreno ou a medida de uma escada apoiada em uma parede.
- Um pintor precisa calcular o comprimento da escada necessária para alcançar o topo de uma parede de 3 metros de altura, estando a base da escada a 4 metros da parede. Qual o comprimento mínimo da escada?
- Um fazendeiro precisa calcular a distância diagonal entre dois cantos opostos de um celeiro retangular com 20 metros de comprimento e 15 metros de largura. Calcule a distância diagonal.
- Uma pessoa precisa cortar uma prancha retangular de 24 cm de comprimento e 7 cm de largura em diagonal. Qual será o comprimento do corte diagonal?
Respostas aos Exercícios
| Exercício | Resposta |
|---|---|
| 1 | 10 cm |
| 2 | 13 metros |
| 3 | 18,03 pés (aproximadamente) |
| 4 | 15 cm |
| 5 | 20 cm |
| 6 | 5 metros |
| 7 | 25 metros |
| 8 | 25 cm |
Ilustrações
As ilustrações desempenham um papel crucial na visualização da fórmula da diagonal de um retângulo. Através de representações gráficas, diagramas e imagens, é possível compreender melhor a relação entre os lados do retângulo e a sua diagonal, tornando o conceito mais acessível e intuitivo. As imagens permitem visualizar a aplicação prática da fórmula em diferentes contextos e ajudar a consolidar o entendimento do tema.
Gráficos Cartesianos
Os gráficos cartesianos fornecem uma representação geométrica da fórmula da diagonal em um plano cartesiano. A disposição dos pontos dos vértices do retângulo (ou quadrado) sobre os eixos coordenados permite visualizar a relação entre as coordenadas dos pontos e a diagonal. A diagonal é representada como uma linha reta que conecta dois vértices opostos.
Um exemplo prático seria um gráfico com um retângulo cujos vértices são (0,0), (a,0), (a,b), e (0,b). A diagonal conectaria o ponto (0,0) ao ponto (a,b). Os eixos coordenados seriam claramente identificados, e os pontos dos vértices estariam posicionados e rotulados corretamente, facilitando a compreensão da relação entre as variáveis.
Diagramas de Retângulos/Quadrados
Diagramas de retângulos/quadrados são úteis para ilustrar as dimensões (lados) do retângulo de forma clara. As dimensões, comprimento (a) e largura (b), são explicitamente indicadas, seja por meio de variáveis ou valores numéricos. A diagonal é destacada com uma linha mais espessa ou de cor diferente, destacando a sua importância na relação com os lados.
Um exemplo seria um retângulo com as dimensões “a” e “b” marcadas. A diagonal seria representada com uma linha vermelha mais espessa, enfatizando a sua relação com os lados. Isso torna mais intuitivo o cálculo da diagonal, visto que o diagrama visualiza as relações entre os componentes da fórmula.
Imagens 3D (Opcional)
Imagens tridimensionais, como um prisma retangular ou cubo, oferecem uma perspectiva mais completa da diagonal. A imagem em perspectiva permite visualizar a diagonal no espaço tridimensional, facilitando a compreensão da relação entre os lados e a diagonal em um contexto mais abrangente.
A imagem de um prisma retangular, com as dimensões (comprimento, largura e altura) claramente indicadas, mostraria a diagonal como uma linha conectando vértices opostos. A representação tridimensional ajudaria a visualizar como a diagonal se relaciona com as três dimensões do retângulo.
Imagens com Animacões (Opcional)
Animações podem demonstrar dinamicamente a relação entre os lados e a diagonal. A animação mostraria como a diagonal se modifica em relação aos lados do retângulo à medida que as dimensões mudam. Essa visualização dinâmica destaca a relação matemática entre as variáveis.
Por exemplo, uma animação poderia mostrar um retângulo sendo alterado de tamanho, enquanto a diagonal é atualizada em tempo real, mostrando como a fórmula da diagonal se ajusta às novas dimensões.
Imagens com Variáveis
Ilustrações que utilizam variáveis demonstram como a fórmula da diagonal se adapta a diferentes valores dos lados. Ao mostrar diferentes valores para as variáveis (a e b), a ilustração demonstra o resultado correspondente da diagonal, permitindo visualizar a aplicação da fórmula em várias situações.
Um exemplo seria mostrar a diagonal de um retângulo com valores de “a” = 3 e “b” = 4, e a diagonal calculada. Em seguida, outra ilustração com “a” = 5 e “b” = 12, mostrando a diagonal calculada. Essas ilustrações ajudam a perceber a relação entre os valores das variáveis e o resultado da fórmula.
Símbolos e Notação
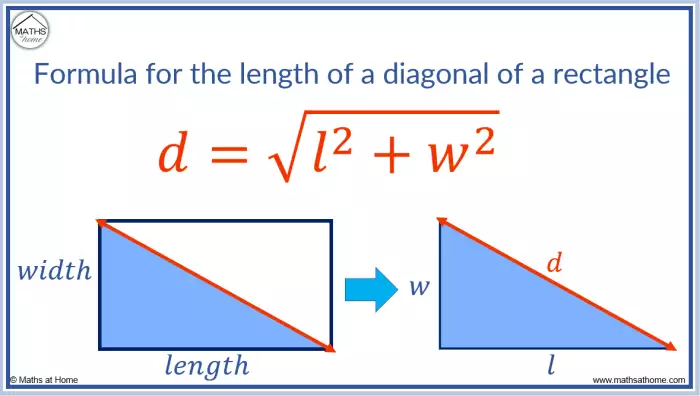
Para compreender e aplicar a fórmula da diagonal de um retângulo, é fundamental entender os símbolos e a notação utilizados. Cada símbolo representa uma grandeza específica do retângulo, permitindo uma interpretação clara e precisa da fórmula.
Definição dos Símbolos
A fórmula da diagonal de um retângulo envolve o comprimento, a largura e a diagonal. Compreender o significado de cada um desses elementos é crucial para aplicar corretamente a fórmula.
| Símbolo | Significado |
|---|---|
| d | Representa o comprimento da diagonal do retângulo. |
| l | Representa o comprimento do retângulo. |
| w | Representa a largura do retângulo. |
A diagonal de um retângulo é a linha que conecta dois vértices opostos do retângulo.
Os símbolos l e w, por exemplo, são utilizados para representar as medidas dos lados do retângulo. A utilização de símbolos específicos, como d, l e w, permite a generalização da fórmula, aplicando-a a qualquer retângulo, independente de suas dimensões. A diagonal d, então, pode ser calculada a partir das medidas do comprimento e largura. A escolha de letras específicas facilita a compreensão e a manipulação da fórmula em diferentes contextos.
Aplicações em Domínios Específicos
A fórmula da diagonal de um retângulo, apesar de parecer uma ferramenta simples, encontra aplicações relevantes em diversas áreas, auxiliando na resolução de problemas práticos e na otimização de projetos. Sua utilização abrange desde cálculos estruturais em engenharia até a determinação de dimensões em design gráfico, permitindo a visualização espacial e a resolução de problemas envolvendo formas retangulares.A compreensão da fórmula da diagonal e suas aplicações práticas permite a tomada de decisões mais assertivas em projetos que envolvem a geometria de retângulos, melhorando a eficiência e a precisão dos resultados.
Aplicações em Engenharia
A engenharia civil e mecânica frequentemente se deparam com situações que exigem o cálculo da diagonal de um retângulo. Em projetos de estruturas, como pontes e edifícios, é crucial determinar a estabilidade e a resistência das peças. A fórmula da diagonal auxilia na verificação de tensões e comprimentos, garantindo a segurança e a eficiência das construções. Por exemplo, o cálculo da diagonal de uma viga pode indicar se a estrutura está sujeita a esforços excessivos.
Além disso, na engenharia mecânica, a fórmula é útil para dimensionar peças e componentes, como parafusos e chapas metálicas. Um exemplo prático seria a determinação do comprimento de uma barra de reforço para um determinado espaço retangular.
Aplicações em Arquitetura
Na arquitetura, a fórmula da diagonal é essencial para o planejamento e execução de projetos. A criação de plantas baixas, a disposição de móveis e a otimização do espaço em ambientes retangulares se beneficiam do cálculo da diagonal. Por exemplo, a medição da diagonal de um cômodo auxilia no planejamento da disposição de móveis, evitando colisões ou falta de espaço.
O projeto de escadas, a definição de corredores e a criação de espaços internos com proporções harmoniosas também se beneficiam desta fórmula.
Aplicações em Design Gráfico
No design gráfico, a fórmula da diagonal é útil para criar composições equilibradas e proporções harmônicas em layouts. A diagonal pode ser usada como uma linha guia para a distribuição de elementos visuais, criando dinâmica e profundidade em uma página ou tela. A fórmula também pode ser usada para determinar as dimensões de imagens ou objetos retangulares para que se encaixem em um layout específico.
Por exemplo, ao criar um pôster retangular, a fórmula da diagonal auxilia na escolha de um tamanho que proporcione uma relação harmoniosa entre as partes.
Em resumo, a fórmula da diagonal de um retângulo em termos de comprimento e largura, baseada no Teorema de Pitágoras, fornece uma solução eficiente para determinar o comprimento da diagonal. Apresentamos exemplos práticos e abordamos a aplicação da fórmula em cenários reais, além de comparar com a diagonal de um quadrado e discutir suas limitações. Esperamos que este conteúdo tenha esclarecido e aprofundado a compreensão sobre este importante conceito geométrico.
Quais as unidades de medida mais comuns para calcular a diagonal de um retângulo?
As unidades de medida mais comuns são centímetros (cm), metros (m), polegadas (pol), milímetros (mm) e pés (ft), dependendo da aplicação.
Como a fórmula da diagonal se relaciona com o Teorema de Pitágoras?
A fórmula da diagonal é uma aplicação direta do Teorema de Pitágoras, onde a diagonal representa a hipotenusa de um triângulo retângulo formado pelos lados do retângulo.
É possível calcular a diagonal de um retângulo com lados negativos?
Não. A fórmula da diagonal utiliza o quadrado dos lados, tornando irrelevante o sinal negativo. As medidas de comprimento e largura devem ser valores positivos.
Quais as limitações da fórmula da diagonal?
A fórmula assume que o retângulo é um polígono plano. Ela não considera situações onde o retângulo pode estar em um espaço tridimensional ou ter alguma deformação.