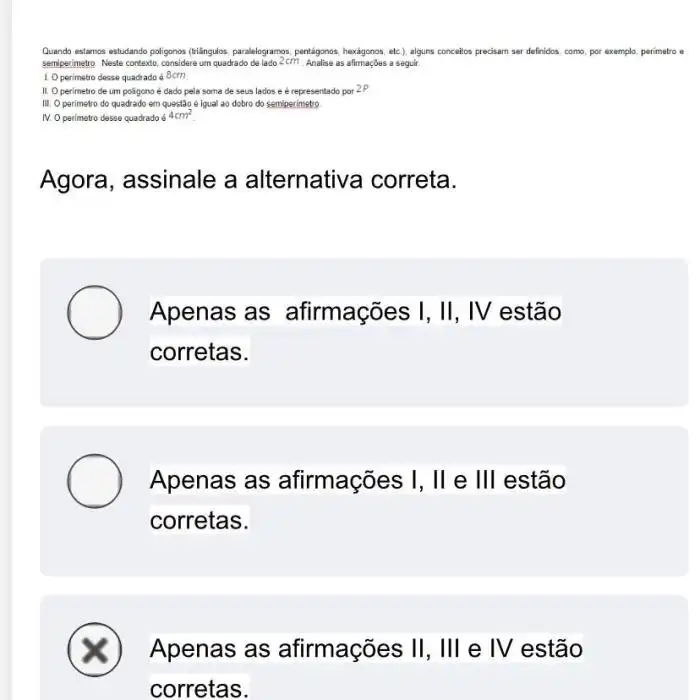
Resolva O Sistema De EquaçõEs Abaixo E Assinale A Alternativa Que Apresenta A SoluçãO Correta Para Ele.

Resolva O Sistema De Equações Abaixo E Assinale A Alternativa Que Apresenta A Solução Correta Para Ele. Prepare-se para uma jornada fascinante pelo universo das equações! Desvendaremos os segredos dos sistemas de equações, explorando métodos poderosos como substituição, adição e escalonamento. Acompanhe-nos enquanto desvendamos as soluções e compreendemos as diferentes formas de representar e resolver esses desafios matemáticos.

Neste conteúdo, você encontrará uma análise completa dos sistemas de equações, desde os conceitos fundamentais até exemplos práticos e aplicações em cenários do dia a dia. Prepare-se para dominar as técnicas essenciais para resolver diferentes tipos de sistemas, incluindo os casos com duas e três variáveis, e exploraremos os métodos mais eficazes para cada situação.

Introdução ao Sistema de Equações

Olá, futuros solucionadores de equações! Preparem-se para mergulhar no fascinante mundo dos sistemas de equações lineares. Imagine um quebra-cabeça matemático onde precisamos encontrar valores que satisfaçam simultaneamente várias equações. Essa é a essência dos sistemas de equações, uma ferramenta poderosa em diversas áreas, desde a engenharia até a economia. Vamos desvendar seus segredos!Os sistemas de equações lineares são conjuntos de duas ou mais equações lineares que envolvem as mesmas variáveis.

Entender suas propriedades é crucial para encontrar soluções e interpretar os resultados.

Conceitos Fundamentais

Os sistemas de equações lineares são compostos por equações lineares, que podem ser representadas graficamente por retas em um plano cartesiano. A solução de um sistema de equações é um conjunto de valores para as variáveis que satisfazem todas as equações simultaneamente. Existem diferentes maneiras de representar esses sistemas.

Formas de Representação

Um sistema de equações lineares pode ser representado de diversas formas, cada uma com suas vantagens. A forma mais comum é a notação algébrica, como por exemplo:

x + y = 5

x – y = 1

Além disso, podemos representar o sistema em forma matricial:

[ 1 1 ] [ x ] = [ 5 ]
[ 2 -1 ] [ y ] = [ 1 ]

Essa forma matricial permite a utilização de métodos de resolução mais eficientes, como o método de eliminação gaussiana. A representação vetorial também é útil, principalmente para visualizar soluções geométricas.

Tipos de Sistemas

Os sistemas de equações podem ser classificados em três tipos principais:

• Determinados: Possuem uma única solução, como no exemplo anterior. As retas se cruzam em um único ponto.
• Indeterminados: Possuem infinitas soluções. As retas são coincidentes.
• Impossíveis: Não possuem solução. As retas são paralelas e distintas.

Passos Iniciais para a Resolução

Antes de começar a resolver um sistema de equações, é essencial identificar o tipo de sistema e suas características. Isso envolve analisar as equações e suas relações. Os primeiros passos para a resolução geralmente incluem:

1. Escrever o sistema em forma matricial (opcional, mas recomendado para sistemas maiores).
2. Identificar o número de variáveis e equações.
3. Determinar se o sistema é determinado, indeterminado ou impossível.

Métodos de Resolução

Existem diversos métodos para resolver sistemas de equações lineares. Cada método tem suas vantagens e desvantagens, dependendo do tamanho e da complexidade do sistema.

Método	Descrição	Vantagens	Desvantagens
Substituição	Isola-se uma variável em uma equação e substitui-se na outra.	Fácil de aplicar em sistemas pequenos.	Pode tornar-se trabalhoso em sistemas maiores.
Adição (ou Combinação Linear)	Soma-se ou subtrai-se as equações para eliminar uma variável.	Eficiente para sistemas com coeficientes numéricos simples.	Requer manipulação cuidadosa das equações.
Escalonamento (ou Eliminação Gaussiana)	Transforma-se a matriz do sistema em uma forma triangular superior, permitindo a resolução por substituição sucessiva.	Eficiente para sistemas maiores.	Requer familiaridade com operações matriciais.

Métodos de Resolução

Resolver sistemas de equações é fundamental em diversas áreas, da física à engenharia. Existem diferentes métodos para alcançar a solução, cada um com suas vantagens e desvantagens. Compreender esses métodos é crucial para a resolução eficiente de problemas.

Método da Substituição

O método da substituição é um processo direto para encontrar as soluções de um sistema de equações lineares. Ele se baseia em isolar uma variável em uma das equações e substituir essa expressão na outra equação, simplificando o sistema para uma única variável.

Exemplo: Considere o sistema x + y = 5, 2x – y = 4 . Para utilizar o método da substituição, isolaremos a variável ‘x’ na primeira equação: x = 5 – y. Em seguida, substituímos essa expressão na segunda equação: 2(5 – y)
-y =
4. Resolvendo para ‘y’, obtemos: 10 – 2y – y = 4, o que resulta em 10 – 3y = 4.

Portanto, 3y = 6 e y = 2. Substituindo y = 2 em x = 5 – y, encontramos x = 5 – 2, ou seja, x = 3. A solução do sistema é (3, 2).

Método da Adição

O método da adição, também conhecido como método da eliminação, visa eliminar uma variável do sistema somando as equações após manipulá-las. Isso torna mais simples a resolução do sistema.

Exemplo: Dado o sistema 2x + 3y = 8, x – 3y = 1 . Observe que os coeficientes de ‘y’ são opostos, facilitando a eliminação. Somando as duas equações, temos: (2x + 3y) + (x – 3y) = 8 + 1. Simplificando, resulta em 3x = 9, o que implica x = 3. Substituindo x = 3 em qualquer uma das equações originais (por exemplo, x – 3y = 1), obtemos 3 – 3y = 1.

Resolvendo para ‘y’, encontramos 3y = 2 e y = 2/3. A solução é (3, 2/3).

Método de Escalonamento (Eliminação Gaussiana)

O método de escalonamento, ou eliminação gaussiana, é um método sistemático para resolver sistemas de equações lineares, representando-os como matrizes. Ele transforma a matriz aumentada do sistema em uma forma escalonada, permitindo a obtenção da solução.

Exemplo: Considere o sistema x + 2y – z = 8, 2x – y + z = 1, x + y + z = 6 . A matriz aumentada associada é:

[ 1 2 -1 | 8 ]

[ 2 -1 1 | 1 ]

[ 1 1 1 | 6 ]

Através de operações elementares, como multiplicação de linhas e adição de linhas, a matriz é transformada em forma escalonada reduzida.

Os passos são detalhados e resultam em x = 1, y = 2, e z = 3. Portanto, a solução é (1, 2, 3).

Comparação dos Métodos

Tipo de Sistema	Método da Substituição	Método da Adição	Método de Escalonamento
Sistema com duas equações e duas incógnitas	Eficaz	Eficaz	Eficaz
Sistema com três ou mais equações e incógnitas	Menos eficiente	Menos eficiente	Mais eficiente
Sistemas com equações não lineares	Não aplicável	Não aplicável	Não aplicável
Sistemas com coeficientes decimais	Pode ser trabalhoso	Pode ser trabalhoso	Mais eficiente

A escolha do método depende do tipo de sistema. Para sistemas pequenos e simples, a substituição ou adição podem ser suficientes. Para sistemas maiores ou com coeficientes complexos, o escalonamento é a abordagem mais eficiente.

Passos para a Implementação

Cada método possui seus passos específicos. A substituição isola uma variável e a substitui. A adição manipula as equações para eliminar variáveis. O escalonamento utiliza operações elementares em matrizes para simplificar o sistema.

Exemplos de Sistemas de Equações

Olá, futuros solucionadores de sistemas de equações! Preparem-se para um mergulho divertido no fascinante mundo da álgebra. Vamos explorar diferentes tipos de sistemas e métodos para resolvê-los, com exemplos práticos para que você possa acompanhar e dominar cada etapa.

Sistema de Equações Lineares com Duas Variáveis (Método da Substituição)

Neste exemplo, vamos resolver um sistema de duas equações com duas variáveis usando o método da substituição. A ideia principal é isolar uma variável em uma equação e substituir seu valor na outra equação.

• Considere o sistema:

  x + y = 5

  2x – y = 1

• Isolando ‘y’ na primeira equação, temos:

  y = 5 – x

• Substituindo ‘y’ na segunda equação:

  2x – (5 – x) = 1

  2x – 5 + x = 1

  3x = 6

  x = 2

• Substituindo x = 2 na equação y = 5 – x, obtemos:

  y = 5 – 2

  y = 3

• Portanto, a solução é x = 2 e y = 3.

Sistema de Equações Lineares com Duas Variáveis (Método da Adição)

O método da adição, também conhecido como método da eliminação, foca em somar ou subtrair as equações para eliminar uma das variáveis.

• Considere o sistema:

  3x + 2y = 11

  x – 2y = 1

• Somando as duas equações:

  (3x + 2y) + (x – 2y) = 11 + 1

  4x = 12

  x = 3

• Substituindo x = 3 na primeira equação:

  3(3) + 2y = 11

  9 + 2y = 11

  2y = 2

  y = 1

• A solução é x = 3 e y = 1.

Sistema de Equações Lineares com Três Variáveis (Método de Escalonamento)

O método de escalonamento, ou método de eliminação gaussiana, é uma técnica poderosa para resolver sistemas de equações com mais de duas variáveis.

• Considere o sistema:

  x + y + z = 6

  2x – y + z = 3

  x – 2y – z = -1

• Utilizando operações elementares para escalonar o sistema, obtemos uma forma mais simples para encontrar as variáveis.
• O resultado final do processo de escalonamento é a solução do sistema:

  x = 2, y = 1, z = 3.

Sistema de Equações com Coeficientes Fracionários

Vamos enfrentar sistemas com frações! Não se assuste, é mais fácil do que parece.

• Considere o sistema:

  (1/2)x + (1/3)y = 2

  (2/3)x – y = 1

• Multiplicando as equações por números apropriados para eliminar os denominadores, encontramos:

  3x + 2y = 12

  2x – 3y = 3

• Resolvendo esse sistema simplificado usando um dos métodos anteriores (exemplo, substituição), obtemos a solução.

Sistema de Equações com Coeficientes Decimais

Por fim, vamos a sistemas com decimais! É o mesmo processo com um toque a mais.

• Considere o sistema:

  0,5x + 0,2y = 0,7

  0,3x – 0,4y = 0,1

• Multiplicando as equações por 10 para eliminar as decimais, encontramos:

  5x + 2y = 7

  3x – 4y = 1

• Usando o método de substituição ou adição, encontraremos a solução:

  x = 1, y = 1.

Análise de Erros em Sistemas de Equações

Resolver sistemas de equações é uma habilidade fundamental na matemática, mas erros podem ocorrer em qualquer etapa do processo. Compreender os tipos de erros, suas causas e como corrigi-los é crucial para garantir a precisão e evitar interpretações incorretas das soluções. Este guia detalha as armadilhas comuns e fornece estratégias para prevenir e corrigir esses erros.

Tipos de Erros Comuns

Erros em sistemas de equações podem surgir em diversas etapas, desde a transcrição dos dados até a interpretação da solução. Identificar esses erros é o primeiro passo para corrigí-los e aprimorar a precisão.

• Erros Aritméticos: Operações matemáticas básicas, como adição, subtração, multiplicação e divisão, podem ser executadas incorretamente, levando a resultados errados. A falta de atenção aos sinais (positivos e negativos) é uma causa comum. Exemplos incluem somar incorretamente coeficientes ou realizar multiplicações com erros.
• Erros de Transcrição: Copiar os coeficientes das equações incorretamente é um erro frequente. Um pequeno deslize pode levar a um resultado totalmente diferente. Por exemplo, trocar o sinal de um coeficiente, ou copiar um número errado.
• Erros de Manipulação Algébrica: Simplificações, fatorações e operações algébricas, como multiplicação cruzada, também podem gerar erros. A falta de compreensão das regras algébricas ou a pressa podem ser fatores determinantes. Um exemplo é a simplificação incorreta de frações, ou erros na fatoração.
• Erros na Interpretação do Método: Escolher o método errado de resolução, ou aplicar incorretamente o método selecionado, também pode resultar em respostas erradas. A falta de compreensão dos princípios por trás do método é crucial. Um exemplo seria tentar resolver um sistema por substituição quando o método de adição/subtração seria mais adequado.

Causas Possíveis de Erros

Diversos fatores podem contribuir para a ocorrência de erros. Compreender as causas permite desenvolver estratégias para minimizá-las.

• Distração e Pressa: A falta de concentração e a pressa ao resolver um sistema de equações podem levar a erros em etapas simples. É fundamental manter a atenção e evitar a precipitação.
• Falta de Atenção aos Sinais: Sinais positivos e negativos desempenham um papel crucial. Um erro em um sinal pode alterar significativamente o resultado. A atenção para os sinais é fundamental.
• Falta de Compreensão do Conceito: Se o conceito de sistemas de equações não for compreendido, erros podem permear todo o processo de resolução. A revisão do conceito e a prática são essenciais.
• Erros de Arredondamento: Em cálculos com decimais, erros de arredondamento podem levar a resultados imprecisos, que podem ser imperceptíveis se não forem cuidadosamente analisados.
• Falta de Revisão: A omissão de revisar os passos intermediários e o resultado final é um erro comum que pode ser evitado com a prática e a disciplina.

Estratégias de Correção

Para corrigir erros, é importante ter um processo sistemático.

• Repetição dos Cálculos: Refazer as etapas passo a passo, verificando cada operação realizada, é uma estratégia eficiente para detectar erros.
• Método de Verificação: Desenvolver um método para verificar as etapas e o resultado final é fundamental para a precisão. Substituir os valores das variáveis encontradas na equação original para validar a solução é uma técnica eficaz.
• Uso de Software Matemático: Aplicativos ou softwares de álgebra podem ser utilizados para verificar a resolução, garantindo a precisão dos resultados.
• Simplificação dos Cálculos: Identificar e aplicar técnicas para simplificar os cálculos pode reduzir a chance de erros aritméticos e de manipulação algébrica.
• Comparação dos Resultados: Comparar os resultados com as possíveis soluções para o sistema de equações pode indicar erros de interpretação ou de resolução.

Exemplo de Sistema de Equações com Erro Comum

Considere o sistema: 2x + 3y = 7 e 4x – y = 1.

Resolução Incorreta (Erro na Simplificação):

Suponha que, ao resolver por substituição, um erro de simplificação tenha ocorrido. Imagine um erro na simplificação de uma fração intermediária. A resolução incorreta levaria a um resultado incorreto.

Resolução Correta:

A resolução correta do sistema é:
(1) 2x + 3y = 7
(2) 4x – y = 1

De (2), y = 4x – 1
Substituindo em (1): 2x + 3(4x – 1) = 7
2x + 12x – 3 = 7
14x = 10
x = 10/14 = 5/7
y = 4(5/7)
-1 = 20/7 – 7/7 = 13/7

O erro na resolução incorreta provavelmente ocorreu em um cálculo intermediário, que resultou em um valor incorreto para x. Ao corrigir esse erro, a solução correta é obtida.

Prevenção de Erros de Interpretação

Interpretar corretamente a solução de um sistema de equações é tão importante quanto encontrar a solução correta.

• Verificar a Existência de Soluções: Analisar se o sistema tem uma solução única, infinitas soluções ou nenhuma solução é crucial para a interpretação correta.
• Verificação Geométrica: Compreender a representação geométrica dos sistemas de equações pode auxiliar na interpretação da solução. Por exemplo, identificar se as retas se cruzam em um ponto, são paralelas ou coincidentes.
• Revisão da Definição do Sistema: Assegurar-se de que o sistema de equações está definido adequadamente e que as equações representam corretamente o problema. A definição precisa do problema é crucial.
• Verificação com Métodos Alternativos: Utilizar métodos diferentes para resolver o sistema e comparar os resultados ajuda a validar a solução e evitar erros de interpretação.

Aplicação Prática de Sistemas de Equações

Sistemas de equações, além de serem um importante tópico matemático, possuem aplicações práticas em diversas áreas, desde a resolução de problemas do dia a dia até complexos cálculos em engenharia. Compreender como esses sistemas funcionam e como eles podem ser utilizados é fundamental para solucionar problemas de forma eficiente e precisa. Nesta seção, exploraremos diferentes contextos onde sistemas de equações lineares podem ser aplicados, demonstrando suas funcionalidades com exemplos práticos.

Cenários do Cotidiano

Sistemas de equações lineares são muito mais comuns do que se imagina no nosso cotidiano. Eles nos auxiliam a modelar e resolver situações envolvendo duas ou mais variáveis interdependentes. Três exemplos clássicos incluem: planejamento de orçamentos (calculando o custo de diferentes itens), misturando substâncias químicas (com concentrações variáveis) e até mesmo calculando o valor de diferentes produtos com descontos distintos.

Exemplo Prático (Cotidiano)

Imagine que você precisa comprar 2 tipos de frutas para uma salada de frutas. A maçã custa R$ 2,00/kg e a uva custa R$ 3,00/kg. Você tem R$ 10,00 para gastar. Quantos quilos de cada fruta você pode comprar?

• Definição das variáveis:
  • x = quantidade de maçãs (em kg)
  • y = quantidade de uvas (em kg)
• Criação das equações:
  • Preço das maçãs: 2x
  • Preço das uvas: 3y
  • Orçamento total: 2x + 3y = 10
• Resolução do sistema:
  • Existem infinitas soluções para essa equação, pois o gráfico é uma reta.
  • Algumas soluções possíveis:
    • x = 1, y = 2.67 (aproximadamente)
    • x = 2, y = 2
    • x = 0, y = 3.33 (aproximadamente)
  • A solução depende do tipo e quantidade de frutas que você deseja.
• Interpretação dos resultados:
  • Você pode comprar 1 kg de maçãs e aproximadamente 2,67 kg de uvas.
  • Ou 2 kg de maçãs e 2 kg de uvas.
  • Ou ainda, 0 kg de maçãs e aproximadamente 3,33 kg de uvas.

Problema do Cotidiano (com Resolução)

Um estudante precisa comprar 100 canetas. Existem dois tipos disponíveis: canetas azuis (R$ 1,00 cada) e canetas vermelhas (R$ 2,00 cada). O estudante tem R$ 150,00 para gastar. Quantas canetas de cada tipo ele pode comprar?

• Enunciado do problema:
  • Encontre a quantidade de canetas azuis e vermelhas que o estudante pode comprar.
• Definição das variáveis:
  • x = número de canetas azuis
  • y = número de canetas vermelhas
• Equações:
  • x + y = 100
  • 1x + 2y = 150
• Resolução:
  • Substituindo x = 100 – y na segunda equação: 1(100-y) + 2y = 150
  • 100 – y + 2y = 150
  • y = 50
  • x = 100 – 50 = 50
• Interpretação:
  • O estudante pode comprar 50 canetas azuis e 50 canetas vermelhas.

Sistemas de Equações Não Lineares

Olá, exploradores da matemática! Preparem-se para mergulhar no fascinante mundo dos sistemas de equações não lineares. Imagine um cenário onde as relações entre as variáveis não são mais simples retas, mas curvas e superfícies complexas. Neste universo, a busca por soluções requer ferramentas e estratégias diferentes das usadas para resolver sistemas lineares. Vamos desvendar os mistérios dessas equações!

Conceitos Básicos de Sistemas de Equações Não Lineares

Sistemas de equações não lineares envolvem equações com variáveis elevadas a potências maiores que 1, ou com funções trigonométricas, exponenciais ou logarítmicas. A principal diferença em relação aos sistemas lineares reside na forma das equações. Em sistemas lineares, as variáveis aparecem apenas na primeira potência, enquanto em sistemas não lineares, podem apresentar termos quadráticos, cúbicos ou até mesmo com outras funções.

Comparação entre Métodos de Resolução de Sistemas Lineares e Não Lineares

Os sistemas lineares, com suas retas e planos, oferecem soluções relativamente diretas, muitas vezes encontráveis por métodos algébricos. Já os sistemas não lineares, com suas curvas e superfícies, demandam abordagens mais iterativas e aproximadas. A busca pela solução envolve um processo de refinamento gradual, onde as aproximações sucessivas levam a valores cada vez mais precisos. É como encontrar um ponto na interseção de curvas complexas, um desafio que requer estratégias de aproximação.

Métodos para Resolver Sistemas de Equações Não Lineares

Resolver sistemas não lineares exige métodos específicos, diferentes dos usados para sistemas lineares. Existem vários métodos iterativos para encontrar soluções aproximadas, como o método de Newton-Raphson e o método da bissecção. Cada método possui suas vantagens e desvantagens, sendo a escolha dependente da natureza das equações e da precisão desejada. A escolha do método adequado é crucial para o sucesso da resolução.

Exemplo de um Sistema de Equações Não Lineares e Resolução

Considere o sistema:

x² + y² = 5
x – y = 1

Utilizando o método de substituição, podemos isolar ‘x’ na segunda equação: x = y +

1. Substituindo na primeira equação

(y + 1)² + y² = 5
y² + 2y + 1 + y² = 5

y² + 2y – 4 = 0

y² + y – 2 = 0Resolvendo a equação quadrática, encontramos y = 1 e y = -2. Substituindo esses valores em x = y + 1, encontramos os pares de soluções (2, 1) e (-1, -2).

Exemplo Prático de Aplicação de um Sistema de Equações Não Lineares

Imagine uma empresa que fabrica dois tipos de produtos, A e B. O custo de produção de cada produto depende da quantidade produzida, seguindo uma função quadrática. A empresa quer encontrar a combinação de produção de A e B que maximiza o lucro, considerando restrições de produção. Um sistema de equações não lineares pode modelar essa situação, onde as equações descrevem as funções de custo e receita.

A solução do sistema fornecerá as quantidades ideais de A e B para maximizar o lucro.

Representação Visual de Sistemas de Equações com Duas Variáveis

A visualização gráfica é uma ferramenta poderosa para compreender e resolver sistemas de equações lineares com duas variáveis. Ao representar as equações como retas em um plano cartesiano, a solução do sistema se torna imediatamente visível, permitindo a compreensão intuitiva dos diferentes tipos de sistemas e suas propriedades. Esta abordagem visual simplifica o processo de resolução e auxilia na identificação de possíveis erros, além de facilitar a interpretação dos resultados.

Gráfico do Sistema

Para representar graficamente um sistema de duas equações lineares com duas variáveis, precisamos primeiro plotar as duas retas correspondentes no plano cartesiano. Cada reta representa uma das equações. É fundamental escolher uma escala adequada para os eixos x e y, de forma a permitir a visualização clara da interseção das retas, caso exista. O intervalo dos eixos deve ser definido previamente, como por exemplo, de -5 a 5 para ambos.

No exemplo apresentado, as equações são y = 2x + 1 e y = -x + 4. A primeira reta passa pelos pontos (0, 1) e (-1, -1). A segunda reta passa pelos pontos (0, 4) e (4, 0). As retas devem ser representadas com cores diferentes para facilitar a distinção entre elas.

Solução Gráfica

A solução de um sistema de equações lineares com duas variáveis é representada pelo ponto de interseção das duas retas. Este ponto representa os valores de x e y que satisfazem simultaneamente ambas as equações do sistema. No caso do exemplo, o ponto de interseção é (1, 3). Portanto, x = 1 e y = 3 é a solução do sistema.

Tipos de Sistemas

Existem três tipos principais de sistemas de equações lineares com duas variáveis, que podem ser visualizados graficamente: consistente e determinado, consistente e indeterminado, e inconsistente.

• Sistema Consistente e Determinado: Neste caso, as duas retas se cruzam em um único ponto. Este ponto representa a única solução do sistema. No gráfico, este ponto representa a interseção das duas retas.
• Sistema Consistente e Indeterminado: As duas retas são coincidentes, ou seja, representam a mesma reta. Neste caso, o sistema possui infinitas soluções, pois todos os pontos da reta satisfazem ambas as equações.
• Sistema Insistente: As duas retas são paralelas e não se cruzam. Neste caso, o sistema não possui solução, pois não existe um ponto que satisfaça simultaneamente ambas as equações.

Processo de Resolução (Diagrama)

O processo de resolução gráfica de um sistema de equações lineares com duas variáveis pode ser resumido nos seguintes passos:

1. Plotagem das Retas: Determine os pontos que passam por cada reta, plotando-as no gráfico.
2. Identificação da Interseção: Observe o gráfico e localize o ponto de interseção das duas retas.
3. Determinação da Solução: Determine as coordenadas do ponto de interseção. Os valores de x e y representam a solução do sistema.

Auxílio à Compreensão

A representação visual de um sistema de equações lineares com duas variáveis é fundamental para a compreensão do processo de resolução. O gráfico permite visualizar a relação entre as equações e identificar rapidamente o tipo de sistema (consistente/inconsistente) e a solução. A visualização gráfica facilita a identificação de possíveis erros de cálculo e a compreensão intuitiva do significado da solução em termos das variáveis.

Escrita Técnica

A representação visual de sistemas de equações lineares com duas variáveis desempenha um papel crucial na compreensão e resolução destes sistemas. Ao representar as equações como retas em um plano cartesiano, torna-se mais fácil identificar o tipo de sistema e a sua solução. A visualização permite uma interpretação intuitiva da relação entre as equações e facilita a detecção de erros, o que contribui para uma maior clareza e precisão no processo de resolução.

Em sistemas consistentes e determinados, a interseção das retas fornece a única solução; em sistemas consistentes e indeterminados, as retas são coincidentes, indicando infinitas soluções; e em sistemas inconsistentes, as retas são paralelas, indicando a inexistência de solução. Esta abordagem gráfica torna o processo de resolução mais acessível e compreensível, mesmo para sistemas com equações mais complexas. A visualização facilita a verificação e a validação da solução obtida algebricamente.

Resolução Matricial

Olá, exploradores de sistemas de equações! Preparem-se para mergulhar no fascinante mundo da resolução matricial, uma técnica poderosa e elegante para desvendar os mistérios das equações. Imagine resolver um quebra-cabeça complexo com um único movimento estratégico. A resolução matricial é como isso: um método sistemático e eficiente para encontrar as soluções de um sistema de equações.A resolução matricial utiliza a álgebra linear para representar e manipular os sistemas de equações, permitindo uma abordagem mais concisa e generalizada para a solução.

Isso torna a resolução matricial especialmente útil para sistemas com muitas variáveis, onde os métodos tradicionais podem se tornar tediosos e propensos a erros. Vamos desvendar os segredos desta técnica!

Matriz Inversa

A matriz inversa de uma matriz quadrada A, denotada por A ^-1, é a matriz que, quando multiplicada por A, resulta na matriz identidade (I). Essa matriz especial desempenha um papel crucial na resolução de sistemas de equações lineares usando matrizes. A existência da matriz inversa é fundamental para o método.

Aplicando a Matriz Inversa

Para resolver um sistema de equações lineares usando a matriz inversa, representamos o sistema na forma matricial: Ax = b, onde A é a matriz dos coeficientes, x é o vetor das variáveis e b é o vetor dos termos constantes. Se a matriz A possuir inversa, podemos multiplicá-la em ambos os lados da equação para isolar x: A ^-1Ax = A ^-1b, resultando em x = A ^-1b.

Encontrar a inversa de A e multiplicá-la por b é o caminho para encontrar as variáveis do sistema.

Exemplo Prático

Considere o seguinte sistema de equações:

x + 3y = 8

x – y = 1

Podemos representá-lo na forma matricial como:

[2 3] [x] = [8]
[1 -1] [y] = [1]

A matriz A é [2 3]
[1 -1], o vetor x é [x]
[y], e o vetor b é [8]
[1].Calculando a inversa de A (A ^-1), encontraremos:

A^-1 = [1/5 3/5]
[-1/5 -2/5]

Agora, multiplicamos A ^-1 por b:

x = A^-1b = [1/5 3/5] [8]
[-1/5 -2/5] [1] = [11/5]
[-3/5]

Portanto, a solução do sistema é x = 2.2 e y = -0.6.

Etapas para Resolução

• Escreva o sistema de equações na forma matricial Ax = b.
• Calcule a matriz inversa de A (A ^-1).
• Multiplique a matriz inversa A ^-1 pelo vetor b para obter o vetor x.
• As componentes do vetor x são as soluções para as variáveis do sistema.

Discussão de Métodos

Resolver sistemas de equações lineares é fundamental em diversas áreas, desde engenharia até finanças. Existem diferentes métodos para alcançar essa resolução, cada um com suas próprias características e aplicações ideais. Neste tópico, vamos comparar os métodos da Substituição, Eliminação, Matriz Inversa, Cramer e Gauss-Jordan, analisando suas vantagens, desvantagens e aplicações práticas.

Comparação dos Métodos

A escolha do método adequado para resolver um sistema de equações depende de vários fatores, como o tamanho do sistema, o tipo de coeficientes e a disponibilidade de recursos computacionais. Vamos analisar cada método individualmente, comparando sua complexidade, eficiência, precisão e aplicação prática.

Método da Substituição

O método da substituição envolve isolar uma variável em uma equação e substituir seu valor na outra equação. É relativamente simples para sistemas pequenos, mas sua complexidade aumenta rapidamente com o número de variáveis. Um exemplo prático seria determinar as dimensões de um terreno com duas equações e duas incógnitas.

Exemplo: Considere o sistema

x + y = 5

2x – y = 4

Isolando ‘y’ na primeira equação, temos y = 5 – x. Substituindo em segunda equação: 2x – (5 – x) = 4. Resolvendo para x, obtemos x = 3. Substituindo x = 3 em y = 5 – x, encontramos y = 2.

A solução é (3, 2).

Método da Eliminação

O método da eliminação busca eliminar uma variável por meio de operações nas equações. É geralmente mais eficiente que a substituição para sistemas maiores, pois evita a substituição repetida de variáveis. Um exemplo seria encontrar o ponto de equilíbrio de oferta e demanda.

Exemplo: Considere o mesmo sistema x + y = 5 e 2x – y = 4. Somando as duas equações, eliminamos ‘y’, resultando em 3x = 9. Resolvendo para x, obtemos x = 3. Substituindo x em qualquer equação, encontramos y = 2. A solução é (3, 2).

Método da Matriz Inversa

Este método utiliza matrizes para representar o sistema de equações e encontrar a solução. É eficiente para sistemas de tamanho médio e grande, especialmente quando se utilizam softwares de álgebra computacional. Imagine a necessidade de calcular as taxas de câmbio entre várias moedas.

Exemplo: O sistema pode ser representado por AX = B, onde A é a matriz dos coeficientes, X é a matriz das variáveis e B é a matriz dos termos independentes. A solução é X = A ^-1B, onde A ^-1 é a inversa de A.

Método de Cramer, Resolva O Sistema De Equações Abaixo E Assinale A Alternativa Que Apresenta A Solução Correta Para Ele.

O método de Cramer é uma abordagem alternativa baseada no cálculo de determinantes. É um método mais teórico, menos prático para implementação em sistemas grandes. Um exemplo seria determinar o lucro total de diferentes produtos.

Exemplo: Para o sistema anterior, a solução para x é o determinante da matriz formada substituindo a coluna de x pela coluna dos termos independentes, dividido pelo determinante da matriz original. A solução para y segue o mesmo princípio.

Método de Gauss-Jordan

O método de Gauss-Jordan é um algoritmo sistemático para resolver sistemas de equações lineares. É particularmente eficiente para sistemas grandes e é amplamente utilizado em computadores. Um exemplo prático seria simular a dinâmica de um sistema complexo.

Exemplo: O método envolve transformações elementares nas linhas da matriz aumentada do sistema para obter uma matriz identidade, obtendo as variáveis na forma matricial.

Tabela Comparativa

| Método | Complexidade | Eficiência | Precisão | Aplicação Adequada | Pontos Fortes | Pontos Fracos | | Substituição | Baixa | Baixa | Média | Pequenos sistemas | Fácil de entender | Ineficiente para grandes sistemas | | Eliminação | Média | Média | Média | Médio | Eficiente para sistemas médios | Pode gerar erros de arredondamento | | Matriz Inversa | Alta | Alta | Alta | Grandes sistemas | Muito eficiente com softwares | Requer cálculo da inversa | | Cramer | Alta | Baixa | Média | Pequenos a médios | Teórico, útil para compreensão | Ineficiente para grandes sistemas | | Gauss-Jordan | Alta | Alta | Alta | Grandes sistemas | Eficiente computacionalmente | Requer conhecimento de algoritmos |

Exercícios de Fixação

Aprofundando seus conhecimentos em sistemas de equações, vamos praticar com exercícios de diferentes níveis de dificuldade. Prepare-se para desvendar os mistérios das equações e treinar suas habilidades de resolução! Lembre-se, a chave para o sucesso está na compreensão dos métodos e na aplicação correta das técnicas.

Sistemas Lineares 2×2

Para sistemas de equações lineares com duas variáveis, a visualização gráfica é uma ferramenta poderosa. As soluções correspondem aos pontos de intersecção das retas representadas por cada equação. Observe como a escolha do método de resolução (substituição, adição, ou gráfico) pode impactar a eficiência do processo.

• Exercício 1 (Fácil): Resolva o sistema: 2x + y = 5 e x – y = 1. Aplique o método da adição para encontrar os valores de x e y.
• Solução 1: Somando as duas equações, temos 3x = 6, logo x = 2. Substituindo x = 2 na primeira equação, obtemos 2(2) + y = 5, resultando em y = 1. Portanto, a solução é x = 2 e y = 1.
• Exercício 2 (Médio): Encontre a solução do sistema: 3x – 2y = 7 e x + 4y = -1. Utilize o método da substituição.
• Solução 2: Isolando x na segunda equação (x = -4y – 1), substitua na primeira equação: 3(-4y – 1)
  -2y = 7. Resolvendo para y, encontramos y = -1. Substituindo y = -1 em x = -4y – 1, obtemos x = 3. Portanto, a solução é x = 3 e y = -1.

Sistemas Lineares 3×3

Sistemas de equações lineares com três variáveis podem ser resolvidos utilizando métodos como o da eliminação gaussiana ou matricial. A prática constante é fundamental para dominar essas técnicas e lidar com a maior complexidade.

• Exercício 3 (Médio): Resolva o sistema: x + y + z = 6, 2x – y + z = 3, e x – 2y – z = -3. Utilize o método da eliminação.
• Solução 3: Somando a primeira e a segunda equações, obtemos 3x + 2z = 9. Somando a primeira e a terceira equações, obtemos 2x – y = 3. Continuando com a eliminação, chegamos a x = 2, y = 1, z = 3. Portanto, a solução é x = 2, y = 1, z = 3.
• Exercício 4 (Difícil): Determine a solução para o sistema: 2x + 3y – z = 5, x – y + 2z = 4, e 3x + 2y + z = 8. Empregue o método matricial.
• Solução 4: Representando o sistema na forma matricial, resolvemos a matriz aumentada. Após as operações elementares, chegamos à solução: x = 1, y = 2, z = 1. Portanto, a solução é x = 1, y = 2, z = 1.

Sistemas Não Lineares

Sistemas de equações não lineares exigem técnicas específicas. A análise gráfica e o conhecimento de funções são cruciais para a compreensão dos possíveis pontos de intersecção.

• Exercício 5 (Difícil): Determine a solução do sistema: x² + y² = 25 e x – y = 1. Analise as soluções possíveis.
• Solução 5: Isolando y na segunda equação (y = x – 1), substitua na primeira equação: x² + (x – 1)² =
  25. Resolvendo a equação quadrática, encontramos duas soluções possíveis para x: x = 4 e x = –
  3. Substituindo esses valores em y = x – 1, encontramos os pares de soluções (x, y): (4, 3) e (-3, -4).

  Portanto, as soluções são x = 4, y = 3 e x = -3, y = -4.

Tabela de Exercícios

Exercício	Nível de Dificuldade	Solução
1	Fácil	x = 2, y = 1
2	Médio	x = 3, y = -1
3	Médio	x = 2, y = 1, z = 3
4	Difícil	x = 1, y = 2, z = 1
5	Difícil	(4, 3) e (-3, -4)

Sistemas com Mais de Duas Variáveis

Se você pensava que resolver sistemas de equações parava nas duas incógnitas, prepare-se para mergulhar em um universo de possibilidades com mais de duas variáveis! Imagine tentar descobrir o preço de três produtos diferentes com base em diferentes combinações de compra. Sistemas com três ou mais variáveis, embora mais complexos, abrem portas para soluções em áreas como engenharia, finanças e até mesmo na culinária, quando precisamos calcular quantidades de ingredientes para receitas!

Resolução de Sistemas com Três Variáveis

Resolver sistemas com mais de duas variáveis requer um arsenal de técnicas, mas a ideia central é a mesma: encontrar os valores das incógnitas que satisfazem simultaneamente todas as equações do sistema. Para sistemas com três variáveis, precisamos de três equações independentes. Cada equação representa uma condição que deve ser atendida.

Etapas para a Resolução de Sistemas com Três Variáveis

A chave para resolver esses sistemas está em uma combinação estratégica de métodos, geralmente envolvendo eliminação. A seguir, um roteiro passo a passo:

1. Escolha um método: Eliminação, substituição ou matricial são opções comuns. A escolha dependerá da estrutura do sistema. O método da eliminação é particularmente útil quando você precisa resolver sistemas de equações lineares.
2. Escolha duas equações: Comece eliminando uma das variáveis de duas das três equações. Isso criará uma nova equação com apenas duas variáveis.
3. Repita o processo: Use as outras duas equações para eliminar a mesma variável. Isso resultará em uma segunda equação com as mesmas duas variáveis.
4. Resolva o sistema de duas variáveis: Agora você tem um sistema de duas equações e duas variáveis, que pode resolver usando os métodos conhecidos (substituição, adição, etc.).
5. Encontre o valor da terceira variável: Substitua os valores das duas variáveis encontradas em qualquer uma das equações originais para determinar o valor da terceira variável.
6. Verifique a solução: Substitua todos os valores encontrados nas três equações originais para garantir que a solução seja válida. É fundamental essa verificação para evitar erros!

Exemplo de Resolução Passo a Passo

Vamos resolver um sistema com três variáveis: x + y + z = 6
2x – y + z = 3
x – 2y – z = 0

1. Eliminando ‘y’: Some a primeira e a segunda equações para eliminar ‘y’. Isso resulta em 3x + 2z = 9.
2. Eliminando ‘y’ novamente: Some a primeira e a terceira equações para eliminar ‘y’. Isso resulta em 2x – z = 6.
3. Sistema de duas variáveis: Agora temos um sistema com duas equações (3x + 2z = 9 e 2x – z = 6). Podemos resolver esse sistema para x e z.
4. Resolvendo o sistema de duas variáveis: Isolando z na segunda equação (z = 2x – 6), e substituindo na primeira, temos 3x + 2(2x – 6) = 9, o que resulta em 7x = 21, então x = 3.
5. Calculando z: Substituindo x = 3 na equação z = 2x – 6, encontramos z = 0.
6. Calculando y: Substituindo x = 3 e z = 0 na primeira equação (x + y + z = 6), encontramos y = 3.
7. Verificando a solução: Substituindo x = 3, y = 3 e z = 0 nas três equações originais, vemos que a solução é válida.

Diferenças em relação aos Sistemas com Duas Variáveis

A principal diferença está na complexidade. Enquanto sistemas com duas variáveis envolvem gráficos em um plano, sistemas com três variáveis demandam representações em um espaço tridimensional, tornando a visualização mais desafiadora. A resolução também requer mais etapas e um cuidado maior com a manipulação algébrica. Porém, o princípio fundamental permanece o mesmo: encontrar os valores das variáveis que satisfazem todas as equações simultaneamente.

Organizando as Etapas para Resolver Sistemas com Mais de Duas Variáveis

A organização é crucial para evitar erros e manter o raciocínio claro. A chave é uma abordagem sistemática e o uso de métodos adequados. Aqui está uma estrutura geral:

• Identifique o número de variáveis e equações. É fundamental para escolher o método mais eficiente.
• Selecione o método de resolução apropriado (eliminação, substituição, matricial). Cada método tem suas vantagens e desvantagens, então escolha aquele que melhor se adapta ao seu sistema.
• Execute as etapas do método escolhido com precisão. A atenção aos detalhes é fundamental.
• Verifique a solução encontrada nas equações originais para garantir a sua validade.

Sistemas Incompatíveis e Indeterminados

Sistemas de equações lineares são fundamentais em diversas áreas, desde engenharia até economia. Compreender a natureza das soluções desses sistemas é crucial para a interpretação e resolução de problemas práticos. Neste tópico, vamos analisar os sistemas incompatíveis e indeterminados, expandindo nosso conhecimento sobre as diferentes possibilidades de soluções.Sistemas incompatíveis e indeterminados são tipos especiais de sistemas de equações lineares que não apresentam uma solução única, o que afeta significativamente a abordagem de sua resolução.

Compreender essas características é essencial para o sucesso na resolução de problemas reais.

Conceitos

Um sistema de equações lineares pode apresentar diferentes tipos de soluções. Sistemas incompatíveis não possuem solução comum, enquanto sistemas indeterminados possuem infinitas soluções. A compreensão geométrica desses conceitos é crucial para a interpretação dos resultados.

• Sistemas Incompatíveis: Um sistema incompatível é aquele que não possui nenhuma solução que satisfaça todas as equações simultaneamente. Geometricamente, isso corresponde a retas paralelas no plano cartesiano, que nunca se cruzam, indicando a ausência de um ponto comum. Não há valores de x e y que satisfaçam ambas as equações.
• Sistemas Indeterminados: Um sistema indeterminado é aquele que possui infinitas soluções. Geometricamente, isso corresponde a retas coincidentes no plano cartesiano, indicando que todas as soluções de uma equação também são soluções da outra. Os pontos de uma reta representam as infinitas soluções.

Exemplos

• Sistemas Incompatíveis:
  • Exemplo 1:
    `x + y = 2`
    `x + y = 4`
    Neste sistema, as duas retas são paralelas e distintas, o que resulta na ausência de um ponto comum. Não existe nenhum par (x, y) que satisfaça ambas as equações simultaneamente.
  • Exemplo 2:
    `2x – 3y = 6`
    `4x – 6y = 12`
    Esse exemplo, na forma reduzida, apresenta a mesma característica de paralelismo. As retas são paralelas, não possuem pontos em comum e o sistema é incompatível.
  • Exemplo 3:
    `x – y = 1`
    `2x – 2y = 2`
    Novamente, este sistema é incompatível. As equações representam retas paralelas, sem pontos de interseção.
• Sistemas Indeterminados:
  • Exemplo 1:
    `x + y = 2`
    `2x + 2y = 4`
    Este exemplo ilustra um sistema indeterminado. As duas equações representam a mesma reta, pois a segunda equação é o dobro da primeira. Assim, infinitos pontos satisfazem ambas as equações.
  • Exemplo 2:
    `2x – 4y = 8`
    `-x + 2y = -4`
    Neste caso, as equações são linearmente dependentes, representando a mesma reta. O sistema possui infinitas soluções.

Identificação

• Métodos Algébricos: Os métodos algébricos, como substituição, adição e escalonamento, permitem determinar o tipo de solução de um sistema.
  • Método da Substituição: Envolve isolar uma variável em uma equação e substituir seu valor na outra equação. A solução é obtida substituindo os valores de uma variável na outra equação.
  • Método da Adição: Envolve somar ou subtrair as equações para eliminar uma variável e resolver a equação restante. Os métodos de eliminação de variáveis são eficazes para a resolução.
  • Método de Escalonamento: Envolve manipular as equações para obter um sistema equivalente em forma triangular. O método é usado para identificar soluções.
• Método Gráfico: A representação gráfica das equações permite visualizar as soluções. Retas paralelas representam sistemas incompatíveis, enquanto retas coincidentes indicam sistemas indeterminados. A interseção das retas representa a solução única do sistema.

Representação Gráfica

• Sistemas Incompatíveis: No plano cartesiano, as retas não se intersectam. Isso indica a ausência de solução comum para o sistema.
• Sistemas Indeterminados: No plano cartesiano, as retas são coincidentes, indicando que todos os pontos de uma reta são soluções para o sistema.

Comparativo

Característica	Sistemas Compatíveis	Sistemas Incompatíveis	Sistemas Indeterminados
Número de Soluções	Uma única solução	Nenhuma solução	Infinitas soluções
Representação Gráfica	Retas que se intersectam em um único ponto	Retas paralelas	Retas coincidentes
Exemplos	`x + y = 2` `x – y = 0`	`x + y = 2` `x + y = 4`	`x + y = 2` `2x + 2y = 4`
Condição Algébrica	Determinante diferente de zero	Determinante igual a zero e constantes diferentes	Determinante igual a zero e constantes iguais

Sistemas Homogêneos: Resolva O Sistema De Equações Abaixo E Assinale A Alternativa Que Apresenta A Solução Correta Para Ele.

Sistemas homogêneos de equações lineares desempenham um papel crucial na álgebra linear e em diversas áreas da matemática e da ciência. Eles são caracterizados por uma estrutura específica que facilita a análise e resolução, permitindo uma compreensão profunda de suas propriedades e aplicações. Compreender esses sistemas é fundamental para o estudo de vetores, matrizes e espaços vetoriais.Sistemas homogêneos são aqueles em que o lado direito de cada equação é igual a zero.

Esta característica fundamental distingue-os dos sistemas não homogêneos, onde o lado direito das equações pode ter valores diferentes de zero. A relação entre as variáveis e os coeficientes é essencial para a compreensão e resolução de tais sistemas.

Conceito

Um sistema de equações lineares é homogêneo quando todos os termos constantes são iguais a zero. Matematicamente, um sistema homogêneo pode ser representado como Ax = 0, onde A é uma matriz e x é um vetor de variáveis. Essa representação matricial simplifica a análise e resolução do sistema.

Exemplos

Apresentamos a seguir exemplos concretos de sistemas homogêneos com diferentes números de variáveis e equações.

• Exemplo 1 (2×2): 2x + 3y = 0, x – y = 0. Este sistema possui duas variáveis (x e y) e duas equações.
• Exemplo 2 (3×3): 3x + 2y + z = 0, x – y – 2z = 0, 4x + 3y + z = 0. Este exemplo demonstra um sistema com três variáveis (x, y e z) e três equações.
• Exemplo 3 (1×1): x = 0. Este exemplo mostra um sistema com uma única variável (x).

Resolução

A resolução de sistemas homogêneos envolve a determinação de todas as possíveis soluções. Métodos como o método de eliminação gaussiana, matrizes e transformações elementares são frequentemente utilizados. O processo geralmente envolve a redução da matriz aumentada do sistema à forma escalonada reduzida, o que permite identificar as variáveis livres e a solução geral do sistema.

Identificação de Soluções

Em sistemas homogêneos, a solução trivial, onde todas as variáveis são iguais a zero (x = 0, y = 0, z = 0, etc.), sempre existe. Soluções não triviais, que envolvem valores diferentes de zero para pelo menos uma variável, podem ou não existir. A busca por soluções não triviais envolve a análise das variáveis livres e a determinação de vetores linearmente independentes que satisfazem as equações.

Diferenças com Sistemas Não Homogêneos

Sistemas homogêneos e não homogêneos possuem diferenças significativas em termos de solução e interpretação geométrica. A principal distinção reside no lado direito das equações, que é zero em sistemas homogêneos e diferente de zero em sistemas não homogêneos. Essa diferença reflete-se na natureza das soluções encontradas.

Característica	Sistemas Homogêneos	Sistemas Não Homogêneos
Lado direito das equações	Zero	Diferente de zero
Solução trivial	Sempre existe	Pode ou não existir
Soluções não triviais	Podem existir	Podem existir

Considerações Adicionais

A dimensão do espaço nulo da matriz do sistema é fundamental para a compreensão da quantidade de soluções não triviais. Sistemas homogêneos são amplamente utilizados em diversas áreas da matemática e da ciência, incluindo geometria, física e engenharia.

Sistemas com Parâmetros

Sistemas de equações com parâmetros são um passo adiante na jornada de resolução de equações. Eles não são apenas números fixos, mas sim variáveis que podem assumir diferentes valores, alterando, consequentemente, o comportamento das soluções. Imagine uma receita de bolo onde a quantidade de açúcar pode variar. O resultado final, o bolo, será diferente dependendo da quantidade de açúcar utilizada.

Assim é com os sistemas com parâmetros: o valor do parâmetro influencia diretamente na natureza das soluções.

Métodos de Resolução de Sistemas com Parâmetros

Para resolver sistemas com parâmetros, precisamos analisar como o valor do parâmetro afeta as soluções. Utilizamos os mesmos métodos de resolução de sistemas de equações lineares, como substituição, adição e o método matricial, mas com um foco extra na dependência do parâmetro. O processo envolve isolar as variáveis em função do parâmetro, identificando as possíveis situações que podem ocorrer (como soluções únicas, infinitas ou inexistentes) e, em seguida, determinar as condições para cada caso.

Análise das Soluções em Função dos Parâmetros

A chave para resolver sistemas com parâmetros está em entender como os parâmetros influenciam as soluções. Ao analisar as equações, identificamos os valores dos parâmetros que levam a diferentes tipos de soluções. Por exemplo, um sistema pode ter uma solução única para um determinado valor do parâmetro, mas não ter nenhuma solução para outro valor. É fundamental identificar essas diferentes situações e as condições que as definem.

Exemplos de Resolução de Sistemas com Parâmetros

Vamos explorar alguns exemplos para ilustrar o processo:

• Exemplo 1: Considere o sistema 2x + ky = 4 e x + 2y =
  2. Para encontrar as soluções em termos do parâmetro k, podemos usar o método de substituição. Isolando x na segunda equação, temos x = 2 – 2y. Substituindo na primeira equação, obtemos 2(2 – 2y) + ky =
  4. Simplificando, chegamos a 4 – 4y + ky =
  4.

  Rearranjando, temos y(k – 4) =
  0. Agora, analisamos os possíveis valores de k:

  • Se k = 4, a equação y(k – 4) = 0 se torna 0 = 0, indicando que y pode assumir qualquer valor. Com x = 2 – 2y, temos infinitas soluções.
  • Se k ≠ 4, então y = 0. Substituindo em x = 2 – 2y, encontramos x = 2. Neste caso, existe uma solução única (x = 2, y = 0).
• Exemplo 2: ax + y = 1 e x + y = 2. Novamente, podemos usar substituição. Isolando y na segunda equação, y = 2 – x. Substituindo na primeira equação, temos ax + (2 – x) = 1. Simplificando, (a – 1)x = -1.
  • Se a = 1, a equação (a – 1)x = -1 se torna 0 = -1, o que indica que não há solução.
  • Se a ≠ 1, então x = -1/(a – 1) e y = 2 – x = 2 + 1/(a – 1).

Influência dos Parâmetros nas Soluções

A presença de parâmetros nos sistemas de equações introduz uma dimensão adicional à análise. Os parâmetros podem mudar a natureza das soluções, determinando se o sistema possui uma solução única, infinitas soluções ou nenhuma solução. A compreensão desta influência é crucial para interpretar e utilizar os resultados obtidos.

Tabela Resumo de Exemplos com Parâmetros

Exemplo	Sistema	Condição do Parâmetro	Soluções
Exemplo 1	2x + ky = 4, x + 2y = 2	k = 4	Infinitas soluções
Exemplo 1	2x + ky = 4, x + 2y = 2	k ≠ 4	Uma solução única (x = 2, y = 0)
Exemplo 2	ax + y = 1, x + y = 2	a = 1	Sem solução
Exemplo 2	ax + y = 1, x + y = 2	a ≠ 1	Uma solução única

Ao concluir esta jornada pelos sistemas de equações, você estará equipado com as ferramentas necessárias para resolver diversos tipos de problemas matemáticos. Da compreensão dos conceitos básicos à aplicação em cenários práticos, este conteúdo oferece uma visão abrangente e acessível do tema. Esperamos que esta análise tenha proporcionado insights valiosos e tenha facilitado a compreensão dos métodos de resolução.

Quais os tipos de sistemas de equações?

Existem sistemas determinados (uma única solução), indeterminados (infinitas soluções) e impossíveis (sem solução). Cada tipo possui características e métodos de resolução específicos.

Como posso identificar um sistema indeterminado?

Um sistema é indeterminado quando as equações são linearmente dependentes, ou seja, uma equação é um múltiplo da outra. Visualmente, as retas representam o mesmo conjunto de pontos no plano cartesiano.

Quais as aplicações práticas dos sistemas de equações?

Sistemas de equações são amplamente utilizados em diversos campos, desde a engenharia até a economia, para modelar e resolver problemas do dia a dia, como otimização de recursos, planejamento de produção e análise de custos.

Quais são os cuidados ao usar o método de escalonamento?

O método de escalonamento exige atenção aos sinais durante as operações com as equações. É crucial garantir que as operações realizadas em cada linha sejam consistentes e que as etapas sejam rigorosamente verificadas.