Com Passo a passo para calcular a diagonal de um retângulo usando a geometria., este guia apresenta um método claro e detalhado para determinar a medida da diagonal de um retângulo. A compreensão deste conceito é fundamental em diversas áreas, como arquitetura, engenharia e design, permitindo a resolução de problemas práticos e o cálculo preciso de distâncias. Exploraremos o Teorema de Pitágoras, fórmulas e exemplos práticos, proporcionando uma experiência didática completa.
A geometria plana, através do estudo de formas e figuras, nos permite resolver problemas de cálculo de distâncias e comprimentos em diferentes contextos. Compreender a diagonal de um retângulo é crucial para o desenvolvimento de soluções precisas e eficazes em diversas áreas.
Introdução ao cálculo da diagonal de um retângulo
O cálculo da diagonal de um retângulo é um conceito fundamental na geometria, com aplicações práticas em diversas áreas, desde a arquitetura até a engenharia. Compreender como determinar a medida da diagonal é crucial para a resolução de problemas que envolvem formas retangulares. Este guia fornecerá uma introdução completa ao tema, abordando conceitos geométricos, história e aplicações práticas.A diagonal de um retângulo é o segmento de reta que une dois vértices opostos do retângulo.
Sua determinação é essencial em projetos que necessitam calcular distâncias entre pontos opostos de estruturas retangulares, como paredes, pisos, ou mesmo em cálculos de diagonais de telas de computadores.
Conceitos geométricos relevantes
Um retângulo é um quadrilátero com quatro ângulos retos e lados opostos paralelos e congruentes. Essas propriedades geométricas são fundamentais para o cálculo da diagonal. Os ângulos retos permitem a aplicação do Teorema de Pitágoras, como será demonstrado posteriormente. A congruência dos lados opostos simplifica a análise geométrica.
História do estudo de diagonais em retângulos
O estudo das diagonais em retângulos remonta à antiguidade. Civilizações antigas, como os egípcios e babilônios, utilizavam a geometria para a construção de estruturas e para a medição de terras. A compreensão das propriedades geométricas dos retângulos e de suas diagonais foi crucial para o desenvolvimento de técnicas de construção e medição. O Teorema de Pitágoras, que estabelece a relação entre os lados e a diagonal de um triângulo retângulo, fornece uma ferramenta fundamental para calcular a diagonal de um retângulo.
Fórmulas e conceitos básicos
Para calcular a diagonal de um retângulo, utilizamos o Teorema de Pitágoras. Este teorema afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). Aplicando este teorema a um retângulo, podemos determinar a diagonal.
Teorema de Pitágoras: a² + b² = c² (onde ‘a’ e ‘b’ são os lados do retângulo e ‘c’ é a diagonal).
Guia passo-a-passo para o cálculo da diagonal
Para calcular a diagonal de um retângulo, siga estes passos:
- Identifique os lados do retângulo. Chame-os de ‘a’ e ‘b’.
- Utilize a fórmula do Teorema de Pitágoras: c² = a² + b².
- Substitua os valores conhecidos de ‘a’ e ‘b’ na fórmula.
- Calcule o valor de c².
- Calcule a raiz quadrada de c² para obter o valor da diagonal ‘c’.
Exemplos de aplicação prática
Imagine que você precisa calcular a diagonal de uma sala retangular com 3 metros de largura e 4 metros de comprimento. Aplicando a fórmula, teremos:c² = 3² + 4² = 9 + 16 = 25c = √25 = 5 metros.Portanto, a diagonal da sala mede 5 metros. Este cálculo é fundamental em projetos de arquitetura e engenharia para determinar distâncias e proporções em espaços retangulares.
Teorema de Pitágoras na determinação da diagonal
O Teorema de Pitágoras é uma ferramenta fundamental na geometria, permitindo calcular a relação entre os lados de um triângulo retângulo. Sua aplicação se estende a diversas áreas, incluindo o cálculo da diagonal de um retângulo, um conceito essencial em matemática e aplicações práticas.O teorema estabelece uma relação precisa entre os três lados de um triângulo retângulo. A diagonal de um retângulo pode ser determinada através da aplicação deste teorema, transformando um problema de geometria bidimensional em um cálculo de triângulo retângulo.
Demonstração Geométrica do Teorema de Pitágoras
O Teorema de Pitágoras afirma que, em qualquer triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). Essa relação pode ser visualizada geometricamente. Imagine um quadrado construído sobre cada um dos três lados de um triângulo retângulo. A área do quadrado construído sobre a hipotenusa é igual à soma das áreas dos quadrados construídos sobre os catetos.
Esta demonstração visual demonstra a validade do teorema.
Relação com o Cálculo da Diagonal de um Retângulo
Para calcular a diagonal de um retângulo, podemos utilizar o Teorema de Pitágoras. Um retângulo pode ser dividido em dois triângulos retângulos congruentes, ao traçar a diagonal. Os lados do retângulo correspondem aos catetos do triângulo retângulo, e a diagonal ao lado da hipotenusa. Aplicando o Teorema de Pitágoras, podemos encontrar o comprimento da diagonal.
Métodos para Calcular a Diagonal Usando o Teorema de Pitágoras
Existem diferentes métodos para calcular a diagonal de um retângulo, todos baseados no Teorema de Pitágoras. O método mais comum e direto envolve identificar os lados do retângulo como catetos e a diagonal como a hipotenusa.
Variáveis Envolvidas no Cálculo da Diagonal
As variáveis essenciais para o cálculo da diagonal de um retângulo, utilizando o Teorema de Pitágoras, são:
- Comprimento (l): Representa a medida de um dos lados do retângulo.
- Largura (w): Representa a medida do outro lado do retângulo.
- Diagonal (d): Representa a medida da diagonal do retângulo, que é a hipotenusa do triângulo retângulo formado.
A fórmula resultante, obtida a partir do Teorema de Pitágoras, é: d2 = l2 + w2.
Aplicação Prática em um Retângulo
Imagine um terreno retangular com 6 metros de comprimento e 8 metros de largura. Para calcular a distância diagonal do terreno, podemos aplicar o Teorema de Pitágoras.
d2 = l2 + w2
Substituindo os valores:
d2 = 6 2 + 8 2 = 36 + 64 = 100
Aplicando a raiz quadrada em ambos os lados:
d = √100 = 10
Portanto, a diagonal do terreno mede 10 metros.
Exemplo Numérico
Considere um retângulo com comprimento de 12 cm e largura de 5 cm. Para calcular a diagonal, aplicamos o Teorema de Pitágoras:
d2 = 12 2 + 5 2 = 144 + 25 = 169
d = √169 = 13
A diagonal do retângulo mede 13 cm.
Fórmula para o cálculo da diagonal
Para determinar a medida da diagonal de um retângulo, a fórmula matemática simplifica o processo, permitindo calcular esse valor com precisão e rapidez, dispensando a necessidade de recorrer a métodos mais complexos. Compreender a fórmula e suas variáveis é essencial para aplicações práticas e para consolidar o conhecimento geométrico.
A Fórmula Matemática
A diagonal de um retângulo pode ser calculada utilizando o Teorema de Pitágoras. A fórmula resultante relaciona as medidas dos lados do retângulo com o comprimento da diagonal.
d = √(a² + b²)
Onde:
- d representa o comprimento da diagonal do retângulo.
- a representa a medida do comprimento do retângulo.
- b representa a medida da largura do retângulo.
Derivação da Fórmula
O Teorema de Pitágoras estabelece que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os outros dois lados). Aplicando esse teorema a um retângulo, a diagonal forma a hipotenusa de um triângulo retângulo cujos catetos são os lados do retângulo. A fórmula acima resulta diretamente da aplicação do Teorema de Pitágoras.
Comparação com Outros Métodos
Comparando com métodos mais complexos, a utilização da fórmula simplificada torna o cálculo da diagonal do retângulo muito mais direto. Não há necessidade de usar trigonometria ou outros processos que envolvam cálculos mais elaborados, desde que conheçamos as medidas dos lados.
Exemplos de Aplicação
Para ilustrar a aplicação da fórmula, apresentamos alguns exemplos com diferentes dimensões:
- Exemplo 1: Um retângulo com comprimento (a) igual a 3 cm e largura (b) igual a 4 cm. Aplicando a fórmula, temos d = √(3² + 4²) = √(9 + 16) = √25 = 5 cm. A diagonal do retângulo mede 5 cm.
- Exemplo 2: Um retângulo com comprimento (a) igual a 6 metros e largura (b) igual a 8 metros. d = √(6² + 8²) = √(36 + 64) = √100 = 10 metros. A diagonal do retângulo mede 10 metros.
- Exemplo 3: Um retângulo com comprimento (a) igual a 12 cm e largura (b) igual a 5 cm. d = √(12² + 5²) = √(144 + 25) = √169 = 13 cm. A diagonal do retângulo mede 13 cm.
Tabela de Exemplos Numéricos
A tabela a seguir resume os exemplos apresentados, facilitando a compreensão da aplicação da fórmula.
| Comprimento (a) | Largura (b) | Diagonal (d) |
|---|---|---|
| 3 cm | 4 cm | 5 cm |
| 6 m | 8 m | 10 m |
| 12 cm | 5 cm | 13 cm |
Procedimento passo a passo para o cálculo
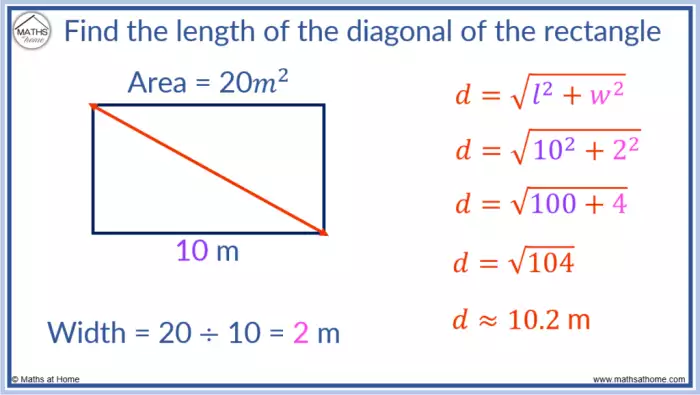
Para determinar a diagonal de um retângulo, podemos recorrer ao Teorema de Pitágoras, uma ferramenta poderosa da geometria. Este procedimento detalhado guiará você através de cada etapa, desde a compreensão dos conceitos até a aplicação prática com exemplos numéricos.
Aplicação do Teorema de Pitágoras
O Teorema de Pitágoras estabelece uma relação fundamental entre os lados de um triângulo retângulo. Em um retângulo, podemos visualizar a diagonal como a hipotenusa de um triângulo retângulo formado pelos lados do retângulo. A fórmula chave para este cálculo é:
c² = a² + b²
onde:
- c representa a diagonal;
- a representa o comprimento;
- b representa a largura.
Cálculo Detalhado da Diagonal, Passo a passo para calcular a diagonal de um retângulo usando a geometria.
Para calcular a diagonal de um retângulo, precisamos conhecer o comprimento e a largura. Seguindo os passos descritos, podemos chegar ao resultado.
- Identificação dos Dados: Inicialmente, identifique o comprimento (a) e a largura (b) do retângulo. Por exemplo, considere um retângulo com comprimento de 6 cm e largura de 8 cm.
- Substituição na Fórmula: Substitua os valores de a e b na fórmula de Pitágoras (c² = a² + b²). No exemplo, teríamos c² = 6² + 8².
- Cálculo das Potências: Calcule os quadrados dos valores de a e b. No exemplo, 6² = 36 e 8² = 64.
- Soma dos Quadrados: Some os resultados obtidos na etapa anterior. No exemplo, 36 + 64 = 100.
- Cálculo da Raiz Quadrada: Calcule a raiz quadrada do resultado da soma (100). A raiz quadrada de 100 é 10.
- Resultado Final: O resultado obtido (10) representa o valor da diagonal (c) do retângulo. No exemplo, a diagonal do retângulo é de 10 cm.
Exemplo Prático
Considere um retângulo com comprimento de 12 cm e largura de 5 cm. Vamos aplicar os passos descritos:
| Etapa | Descrição | Cálculo |
|---|---|---|
| 1 | Identificação dos dados | a = 12 cm, b = 5 cm |
| 2 | Substituição na fórmula | c² = 12² + 5² |
| 3 | Cálculo das potências | c² = 144 + 25 |
| 4 | Soma dos quadrados | c² = 169 |
| 5 | Cálculo da raiz quadrada | c = √169 |
| 6 | Resultado final | c = 13 cm |
O resultado demonstra que a diagonal do retângulo é de 13 cm.
Ilustrações e Visualizações
Para compreender melhor o cálculo da diagonal de um retângulo, é fundamental a visualização gráfica do processo. As ilustrações tornam mais intuitivo o conceito do Teorema de Pitágoras e facilitam a compreensão dos passos envolvidos. Através de representações visuais, é possível observar a relação entre os lados do retângulo e sua diagonal, tornando o aprendizado mais dinâmico e eficaz.As visualizações gráficas, como diagramas e gráficos, demonstram de forma clara a aplicação do Teorema de Pitágoras no cálculo da diagonal.
Isso permite a identificação dos elementos envolvidos no cálculo, promovendo uma compreensão mais aprofundada e prática do conceito.
Representação Gráfica de um Retângulo
A representação gráfica de um retângulo com sua diagonal permite visualizar a relação entre os lados e a diagonal. Um retângulo é um quadrilátero com quatro ângulos retos e lados opostos congruentes. A diagonal de um retângulo é um segmento de reta que une dois vértices opostos.
- Para desenhar um retângulo, trace dois pares de segmentos de reta paralelos e perpendiculares entre si. As linhas horizontais e verticais representarão os lados do retângulo. A interseção das linhas definirá os vértices do retângulo.
- Marque as dimensões (comprimento e largura) do retângulo nos lados correspondentes. Utilize as medidas fornecidas ou crie um exemplo com valores numéricos para melhor compreensão. A clareza na marcação das dimensões é crucial para a compreensão do problema.
- Trace a diagonal do retângulo, conectando dois vértices opostos. A diagonal divide o retângulo em dois triângulos retângulos congruentes. Observe a importância desta divisão para aplicar o Teorema de Pitágoras.
Aplicação do Teorema de Pitágoras
O Teorema de Pitágoras é fundamental para calcular a diagonal de um retângulo. Ele estabelece uma relação entre os três lados de um triângulo retângulo.
O quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os dois lados que formam o ângulo reto).
- Um triângulo retângulo é formado pela diagonal e os dois lados do retângulo. A diagonal é a hipotenusa, e os lados são os catetos. A visualização deste triângulo retângulo é essencial para a aplicação do Teorema de Pitágoras.
- Utilizando as medidas dos lados do retângulo, calcule o quadrado de cada um deles. Some esses valores para obter o quadrado da hipotenusa (diagonal). Calcule a raiz quadrada deste resultado para encontrar a medida da diagonal.
- Apresentar um exemplo numérico, como um retângulo com lados medindo 3 cm e 4 cm. A diagonal será calculada usando a fórmula a² + b² = c², onde a e b são os lados e c é a diagonal.
Diagramas para os Passos do Cálculo
Diagramas que ilustram cada passo do cálculo tornam o processo mais claro e compreensível.
- Desenhe um retângulo com suas dimensões marcadas (por exemplo, comprimento = 6 cm e largura = 8 cm). Marque a diagonal.
- Identifique os lados como catetos e a diagonal como hipotenusa de um triângulo retângulo.
- Aplique a fórmula de Pitágoras para calcular o valor da diagonal.
- Demonstre, graficamente, como os valores são substituídos na fórmula.
- Mostre o resultado final do cálculo da diagonal.
Métodos alternativos para o cálculo da diagonal
Para além do Teorema de Pitágoras, existem outros métodos que podem ser utilizados para calcular a diagonal de um retângulo, utilizando conceitos da trigonometria. Esses métodos oferecem diferentes abordagens, cada uma com suas próprias vantagens e desvantagens. A escolha do método mais adequado dependerá das informações disponíveis e da precisão desejada.A utilização de métodos alternativos, como a trigonometria, permite explorar diferentes relações entre os lados do retângulo e a diagonal, expandindo a compreensão sobre as propriedades geométricas envolvidas.
Trigonometria no Cálculo da Diagonal
A trigonometria fornece uma alternativa ao Teorema de Pitágoras para determinar a diagonal de um retângulo. Utilizando as relações trigonométricas, é possível relacionar os lados do retângulo com a diagonal e um dos ângulos internos do retângulo. Considerando um ângulo agudo (θ) formado entre um lado e a diagonal, é possível aplicar as funções trigonométricas seno, cosseno ou tangente.
Exemplo de Cálculo Utilizando Trigonometria
Considere um retângulo com lados medindo 3 cm e 4 cm. Deseja-se calcular a medida da diagonal.
- Determinação do ângulo: Podemos escolher um dos ângulos agudos. Utilizando a função tangente, temos:
-
tan(θ) = cateto oposto / cateto adjacente = 3 cm / 4 cm = 0,75
- Cálculo do ângulo (θ): Utilizando a função inversa da tangente (arctan ou tan -1), encontramos o ângulo θ:
θ = arctan(0,75) ≈ 36,87°
- Cálculo da diagonal: Utilizando a função seno, podemos encontrar a medida da diagonal (d):
-
sen(θ) = cateto oposto / hipotenusa = 3 cm / d
-
d = 3 cm / sen(36,87°) ≈ 5 cm
Comparação dos Métodos
| Método | Vantagens | Desvantagens |
|---|---|---|
| Teorema de Pitágoras | Direto e simples, não requer conhecimento de trigonometria. | Depende exclusivamente dos comprimentos dos lados. |
| Trigonometria | Explora relações entre os lados e a diagonal, permitindo a resolução de problemas em diferentes contextos. | Reque conhecimento de trigonometria, e a precisão depende da acurácia na determinação do ângulo. |
A escolha do método mais eficiente depende da situação. O Teorema de Pitágoras é mais simples quando se conhecem os comprimentos dos lados. Já a trigonometria permite resolver problemas com informações adicionais, como ângulos.
Erros comuns e como evitá-los
Ao calcular a diagonal de um retângulo utilizando o Teorema de Pitágoras, é crucial prestar atenção aos detalhes para evitar erros. Compreender as possíveis falhas e suas correções é fundamental para garantir a precisão dos resultados. Este tópico apresenta os erros mais frequentes e sugestões para evitá-los, assegurando um cálculo confiável.
Identificação de Erros Comuns
Os erros comuns ao calcular a diagonal de um retângulo geralmente envolvem a aplicação incorreta do Teorema de Pitágoras ou a utilização de valores incorretos para os lados do retângulo. A falta de atenção na utilização da fórmula ou em etapas intermediárias pode levar a resultados imprecisos. É essencial ter clareza sobre os passos envolvidos e a correta aplicação das operações matemáticas.
Causas Possíveis de Erros
Existem diversas causas para os erros no cálculo da diagonal de um retângulo. Uma delas é a confusão entre os termos, como a substituição incorreta dos valores de comprimento e largura na fórmula. Outra causa comum é a execução incorreta das operações aritméticas (adição, subtração, multiplicação e divisão). A utilização de calculadoras ou softwares com imprecisões também pode levar a resultados incorretos.
Por fim, a falta de compreensão do Teorema de Pitágoras pode gerar erros na aplicação da fórmula.
Métodos para Evitar Erros
Para minimizar os erros, é crucial seguir um procedimento passo a passo, verificando cada etapa. É importante usar os valores corretos para os lados do retângulo. A utilização de uma calculadora ou software confiável ajuda a garantir a precisão dos cálculos intermediários. A revisão cuidadosa dos cálculos é essencial para identificar possíveis erros antes de concluir o resultado final.
Um procedimento organizado, com anotações claras, contribui para evitar erros.
Cálculos Incorretos e suas Causas
Um exemplo de cálculo incorreto ocorre quando se usa a fórmula da diagonal como sendo a soma dos lados do retângulo, ao invés da aplicação correta do Teorema de Pitágoras. Essa abordagem ignora a relação fundamental entre os lados e a diagonal. Outro erro é a utilização de valores incorretos para os lados do retângulo no cálculo. Para corrigir, é crucial usar a fórmula correta, a saber, a diagonal é a raiz quadrada da soma dos quadrados dos lados.
Por exemplo, se o retângulo possui lados de 3 cm e 4 cm, a diagonal não é 7 cm, mas sim a raiz quadrada de (3² + 4²) = 5 cm.
Possíveis Problemas com os Cálculos
Problemas com os cálculos podem incluir a utilização de valores incorretos dos lados, a confusão entre as operações matemáticas ou o uso de uma fórmula incorreta. A falta de atenção em etapas intermediárias pode levar a resultados imprecisos.
Tabela de Erros Comuns e suas Correções
| Erro Comum | Descrição | Correção |
|---|---|---|
| Soma dos lados como diagonal | Utilizar a soma dos lados do retângulo como a medida da diagonal. | Utilizar o Teorema de Pitágoras: diagonal² = lado1² + lado2². |
| Substituição incorreta dos valores | Utilizar valores incorretos dos lados na fórmula. | Verificar e substituir os valores de comprimento e largura do retângulo corretamente na fórmula. |
| Cálculo aritmético incorreto | Erros nas operações matemáticas intermediárias. | Revisar cuidadosamente cada etapa do cálculo e usar calculadora ou software para cálculos intermediários, se necessário. |
| Falta de compreensão do Teorema de Pitágoras | Não entender a relação entre os lados e a diagonal. | Reforçar a compreensão do Teorema de Pitágoras e sua aplicação no cálculo da diagonal. |
Aplicação em diferentes contextos: Passo A Passo Para Calcular A Diagonal De Um Retângulo Usando A Geometria.
O cálculo da diagonal de um retângulo, aparentemente um conceito geométrico, encontra aplicações práticas em diversos campos, desde a arquitetura e engenharia até o design e a construção. Compreender como determinar a diagonal é fundamental para a resolução de problemas do dia a dia e para a tomada de decisões em projetos. A aplicação correta deste cálculo garante precisão e eficiência em diversas tarefas.A aplicação do Teorema de Pitágoras para determinar a diagonal de um retângulo é uma ferramenta poderosa para a solução de problemas em diferentes contextos.
A capacidade de calcular a diagonal permite otimizar recursos, garantir a precisão de projetos e prever resultados com maior exatidão.
Aplicações em Arquitetura
O cálculo da diagonal é crucial em projetos arquitetônicos para garantir a correta instalação de elementos estruturais e a precisão na medição de espaços.
- Cálculo de Inclinação de Telhados: Em projetos de construção de telhados, a diagonal do telhado é fundamental para determinar o ângulo de inclinação e a quantidade de material necessário para o revestimento. Um telhado com inclinação incorreta pode levar a problemas de drenagem e à necessidade de reparos futuros. Um exemplo seria calcular a diagonal de um telhado com 5 metros de largura e 10 metros de comprimento para definir a inclinação e o comprimento da estrutura de sustentação.
- Dimensionamento de Paredes e Portas: A diagonal pode ser usada para garantir que portas e janelas se encaixem corretamente em aberturas, evitando problemas de encaixe e desperdícios de materiais. Imagine a necessidade de construir uma parede com uma porta de 2 metros de largura e 2,5 metros de altura. Para garantir o encaixe perfeito, é preciso calcular a diagonal para assegurar que a porta se ajuste corretamente à estrutura da parede.
- Planejamento de Espaços: A diagonal é utilizada para calcular o tamanho de cômodos e a forma como móveis podem ser dispostos em um ambiente. É importante calcular a diagonal para evitar que móveis não se encaixem adequadamente, garantindo o máximo de espaço útil. Um exemplo seria determinar a diagonal de um quarto de 4 metros por 5 metros para definir a melhor disposição de um sofá e uma cama.
Aplicações em Engenharia
Em engenharia, a determinação da diagonal de um retângulo é utilizada em diversos projetos para garantir a precisão e a segurança.
- Análise de Estruturas: Em projetos de pontes e edifícios, a diagonal é usada para calcular as tensões e as forças que atuam sobre as estruturas, garantindo a estabilidade e a segurança do projeto. Por exemplo, na análise de um pilar de concreto de 2 metros por 3 metros, o cálculo da diagonal permite determinar a carga máxima que ele pode suportar antes de sofrer deformações ou colapso.
- Dimensionamento de Tubulações: A diagonal é fundamental para o dimensionamento de tubulações e dutos, garantindo o fluxo adequado de fluidos e a eficiência do sistema. Por exemplo, ao projetar um sistema de drenagem, é preciso calcular a diagonal de um duto para garantir o escoamento correto da água.
- Geometria de Máquinas: O cálculo da diagonal é utilizado no projeto de máquinas e equipamentos para garantir a precisão das peças e a eficiência do funcionamento. Por exemplo, na fabricação de um motor, a diagonal de um bloco de motor precisa ser calculada para garantir que as peças se encaixem perfeitamente e o motor funcione corretamente.
Aplicações em Design
No design, a diagonal pode auxiliar na criação de layouts, na disposição de objetos e na composição visual.
- Design de Interiores: A diagonal é utilizada para criar layouts inovadores e equilibrados. Por exemplo, a disposição de móveis em um espaço de 6 metros por 8 metros utilizando a diagonal para criar um layout dinâmico e atraente.
- Design Gráfico: No design gráfico, a diagonal é usada para criar elementos visuais dinâmicos e atraentes, como a composição de imagens e a disposição de textos. Por exemplo, a utilização de linhas diagonais para destacar elementos importantes em um design gráfico de um logotipo.
- Design de Produtos: A diagonal é fundamental para o dimensionamento e o design de produtos, garantindo que eles se encaixem corretamente e atendam às necessidades dos usuários. Por exemplo, o design de uma caixa para um produto específico necessita do cálculo da diagonal para garantir que o produto se ajuste perfeitamente dentro dela.
Exemplos de exercícios práticos
Para consolidar o aprendizado sobre o cálculo da diagonal de um retângulo, apresentamos a seguir exemplos práticos com diferentes níveis de dificuldade. Cada exemplo inclui uma solução detalhada, permitindo que você acompanhe passo a passo o processo de cálculo e compreenda melhor a aplicação do Teorema de Pitágoras.
Exercícios com Nível Básico
Esses exemplos abordam situações simples, com dados numéricos fáceis de manipular, permitindo que você se familiarize com o método de cálculo da diagonal.
- Exemplo 1: Um retângulo possui lados medindo 3 cm e 4 cm. Calcule o comprimento da diagonal.
Solução:
Para calcular a diagonal de um retângulo, utilizamos o Teorema de Pitágoras. A fórmula é: d² = a² + b², onde d representa a diagonal, e a e b são os lados do retângulo. Neste caso, a = 3 cm e b = 4 cm. Substituindo os valores na fórmula, temos: d² = 3² + 4² = 9 + 16 = 25. Para encontrar d, calculamos a raiz quadrada de 25, resultando em d = 5 cm.
- Exemplo 2: Um retângulo possui lados com 6 metros e 8 metros. Determine o comprimento da diagonal.
Solução:
Aplicando a fórmula d² = a² + b², onde a = 6 m e b = 8 m, temos: d² = 6² + 8² = 36 + 64 = 100. Calculando a raiz quadrada de 100, obtemos d = 10 m.
Exercícios com Nível Intermediário
Os exemplos a seguir apresentam dados um pouco mais complexos, exigindo cálculos mais elaborados.
- Exemplo 3: Um retângulo tem um lado medindo 12 cm e a diagonal medindo 15 cm. Encontre o comprimento do outro lado.
Solução:
Utilizando a fórmula d² = a² + b², com d = 15 cm e a = 12 cm, temos: 15² = 12² + b². Resolvendo a equação: 225 = 144 + b², b² = 81, e b = 9 cm.
- Exemplo 4: Uma sala retangular tem 9 metros de largura e 12 metros de comprimento. Determine a distância entre dois cantos opostos da sala.
Solução:
Neste caso, a largura ( a) é 9 metros e o comprimento ( b) é 12 metros. Aplicando a fórmula d² = a² + b², encontramos: d² = 9² + 12² = 81 + 144 = 225. Portanto, a distância entre os cantos opostos da sala é d = 15 metros.
Considerações Finais e Resumo
Em conclusão desta jornada pelo cálculo da diagonal de um retângulo, revisaremos os conceitos essenciais, resumindo os passos e métodos para uma compreensão mais completa e duradoura. Aprofundaremos a importância do Teorema de Pitágoras e sua aplicação prática.Compreender a determinação da diagonal de um retângulo vai além de uma simples fórmula; é uma aplicação fundamental da geometria e do Teorema de Pitágoras, presente em inúmeras situações práticas, desde a construção de estruturas até o design de produtos.
Conceitos Principais
Os fundamentos para calcular a diagonal de um retângulo estão centrados no Teorema de Pitágoras. Este teorema estabelece uma relação fundamental entre os lados de um triângulo retângulo, permitindo determinar a medida da hipotenusa (a diagonal do retângulo) conhecendo as medidas dos catetos (os lados do retângulo). A aplicação prática deste teorema é crucial para solucionar problemas geométricos e resolver desafios do mundo real.
Passos Essenciais para o Cálculo
Para determinar a diagonal de um retângulo, é necessário seguir um conjunto de passos específicos, baseados na aplicação do Teorema de Pitágoras. A sequência lógica garante a precisão no cálculo e a compreensão dos elementos envolvidos.
- Identificar os comprimentos dos lados do retângulo.
- Utilizar o Teorema de Pitágoras, onde a diagonal (hipotenusa) é calculada como a raiz quadrada da soma dos quadrados dos lados.
- Realizar os cálculos aritméticos, obtendo o valor da diagonal.
Métodos Alternativos e Aplicações
Existem métodos alternativos para calcular a diagonal de um retângulo, como a utilização de tabelas trigonométricas ou software de geometria. Cada método possui suas vantagens e desvantagens, e a escolha do método mais adequado dependerá do contexto da aplicação.
- O Teorema de Pitágoras é o método mais direto e frequentemente utilizado, devido à sua simplicidade e eficácia.
- A utilização de softwares de geometria pode auxiliar em cálculos mais complexos, fornecendo resultados precisos e gráficos para visualização.
Importância do Teorema de Pitágoras
O Teorema de Pitágoras é um princípio fundamental da geometria, com aplicações práticas inúmeras e abrangentes. Sua importância transcende o cálculo da diagonal de um retângulo, sendo essencial para a resolução de problemas que envolvem triângulos retângulos em diversos campos, como engenharia, arquitetura e navegação. A compreensão do teorema permite a resolução de problemas de forma eficiente e precisa.
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Esta relação matemática é a base para o cálculo da diagonal de um retângulo.
Resumo dos Tópicos Abordados
Este conteúdo abrangeu a aplicação do Teorema de Pitágoras para determinar a diagonal de um retângulo. Foram apresentados os passos essenciais para o cálculo, bem como métodos alternativos e a importância deste teorema fundamental na geometria. A compreensão desses tópicos permite o cálculo preciso da diagonal em diversos contextos práticos.
Em resumo, aprendemos a calcular a diagonal de um retângulo usando o Teorema de Pitágoras, analisando fórmulas e métodos alternativos. Este guia passo a passo, com exemplos e ilustrações, oferece uma compreensão abrangente do assunto. Esperamos que este material seja útil para estudantes, profissionais e entusiastas da geometria.
Qual a importância do cálculo da diagonal de um retângulo na prática?
O cálculo da diagonal é fundamental em projetos de arquitetura, engenharia e design, permitindo o cálculo de comprimentos de vigas, diagonais de estruturas e outras aplicações práticas.
Existe mais de um método para calcular a diagonal?
Sim, além do Teorema de Pitágoras, a trigonometria também pode ser utilizada para calcular a diagonal de um retângulo, embora o método de Pitágoras seja o mais comum e direto.
Quais os erros mais comuns ao calcular a diagonal?
Erros comuns incluem a confusão entre as variáveis (comprimento e largura) e o uso incorreto da fórmula de Pitágoras. A atenção aos detalhes e a verificação dos cálculos são cruciais para evitar erros.