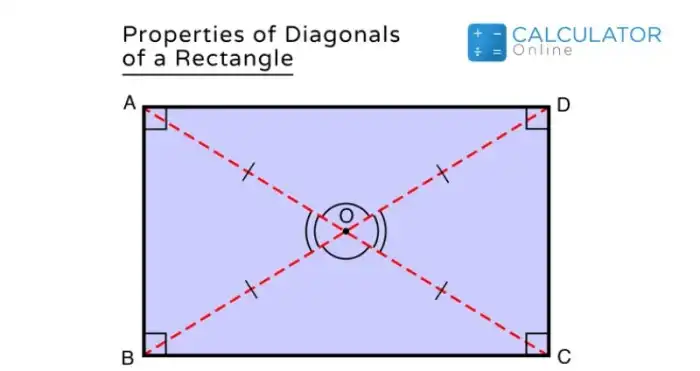
Calculadora de diagonal de retângulo online e passo a passo. Oferece uma solução prática e precisa para calcular a diagonal de um retângulo, seja para projetos de construção, design gráfico ou uso cotidiano. A ferramenta simplifica o processo, comparado a métodos manuais, como o Teorema de Pitágoras, minimizando a possibilidade de erros e fornecendo resultados instantâneos. Com uma interface intuitiva e exemplos claros, a calculadora guia o usuário através de cada etapa, desde a entrada dos dados até a obtenção do resultado final.
A calculadora de diagonal de retângulo online e passo a passo. demonstra a sua versatilidade em diversas aplicações, como calcular a diagonal de um tampo de mesa para garantir a sua estabilidade, determinar o encaixe perfeito de um quadro na parede, ou auxiliar em projetos de engenharia, como o posicionamento de componentes em placas de circuito impresso. A ferramenta online é uma aliada valiosa para quem busca rapidez e precisão nos cálculos de diagonais.
Introdução à Calculadora de Diagonal de Retângulo – Detalhado
A calculadora de diagonal de retângulo é uma ferramenta essencial para diversas aplicações, desde projetos de construção até tarefas cotidianas. Ela simplifica o cálculo da diagonal de um retângulo, fornecendo resultados precisos e evitando cálculos manuais complexos, como o uso do Teorema de Pitágoras. Esta ferramenta se mostra útil em situações que exigem a determinação rápida e precisa da diagonal, reduzindo a margem de erro e o tempo gasto com cálculos.
Utilidades e Aplicações da Calculadora
Esta calculadora de diagonal de retângulo facilita o cálculo em diversos cenários. Sua precisão e rapidez tornam-a uma ferramenta valiosa para profissionais e amadores.
- A calculadora calcula a diagonal de um retângulo com base na sua largura e altura. Esta informação é crucial em diversos projetos, como na construção de estruturas, design gráfico e até mesmo em situações cotidianas. Um exemplo comum é a necessidade de calcular o comprimento de uma diagonal de uma placa retangular, para garantir que ela se encaixa corretamente no espaço disponível.
| Cenário | Descrição | Aplicação da Calculadora |
|---|---|---|
| Projeto de móveis | Cálculo da diagonal de um tampo de mesa retangular para garantir a estabilidade da estrutura. | Determinar o comprimento necessário para a estrutura de sustentação. |
| Design de interiores | Determinar a diagonal de um quadro para garantir que ele se encaixa perfeitamente na parede. | Avaliar a posição do quadro e o espaço necessário. |
| Engenharia | Calcular a diagonal de uma placa de circuito impresso para garantir que os componentes estejam posicionados corretamente. | Determinar o espaço necessário no projeto. |
Comparação com Métodos Manuais
A calculadora de diagonal de retângulo automatiza o cálculo, substituindo a necessidade de cálculos manuais com o Teorema de Pitágoras. Isso economiza tempo e reduz significativamente a probabilidade de erros em cálculos complexos, garantindo maior precisão e confiabilidade. O uso de fórmulas matemáticas manualmente pode ser trabalhoso e propenso a erros de cálculo, principalmente quando lidando com números grandes ou repetitivos.
Passos para Usar a Calculadora
A interface da calculadora é intuitiva e fácil de usar. Para calcular a diagonal de um retângulo, siga estes passos:
- Entrada de Dados: Digite os valores da largura e altura do retângulo nos campos correspondentes.
- Cálculo: Clique no botão “Calcular Diagonal”.
- Saída: A calculadora exibirá o resultado da diagonal calculada.
Exemplo: Um retângulo tem largura de 3cm e altura de 4cm. Qual a sua diagonal? Seguindo os passos acima, a calculadora retornará a diagonal de 5cm.
Formulação Matemática da Diagonal
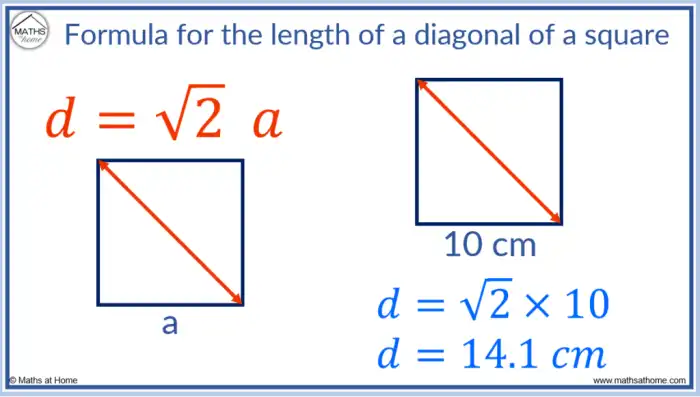
O cálculo da diagonal de um retângulo é uma aplicação direta do Teorema de Pitágoras. Este teorema estabelece uma relação fundamental entre os lados de um triângulo retângulo. Compreender essa relação é essencial para determinar a diagonal de um retângulo, que conecta dois vértices opostos.
Fórmula Matemática
A fórmula para calcular a diagonal de um retângulo é derivada do Teorema de Pitágoras. A fórmula é:
d = √(l² + w²)
onde:
- d representa o comprimento da diagonal;
- l representa o comprimento do retângulo;
- w representa a largura do retângulo.
Derivação da Fórmula
O retângulo pode ser decomposto em dois triângulos retângulos congruentes. A diagonal do retângulo forma a hipotenusa de cada um desses triângulos retângulos. O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos outros dois lados (catetos). Aplicando o Teorema de Pitágoras ao triângulo retângulo formado pela diagonal, o comprimento e a largura do retângulo, obtemos a fórmula d = √(l² + w²).
Variáveis Envolvidas
As variáveis envolvidas no cálculo da diagonal de um retângulo são:
- Comprimento (l): A medida de um dos lados perpendiculares do retângulo. A unidade de medida deve ser consistente.
- Largura (w): A medida do outro lado perpendicular do retângulo. A unidade de medida deve ser consistente com o comprimento.
- Diagonal (d): A distância entre dois vértices opostos do retângulo. A unidade de medida deve ser consistente com o comprimento e a largura.
Unidades de Medida
É crucial manter as unidades de medida consistentes ao longo do cálculo. Se o comprimento e a largura forem expressos em centímetros, a diagonal também deverá ser expressa em centímetros. Por exemplo, se l = 3 cm e w = 4 cm, então d = √(3² + 4²) = 5 cm.
Comparação com outras figuras geométricas
A fórmula para a diagonal de um retângulo (d = √(l² + w²)) difere da fórmula para a diagonal de um quadrado (d = l√2) e de um losango (requerendo o conhecimento de dois lados e o ângulo entre eles). A fórmula para o retângulo incorpora a relação entre comprimento e largura, enquanto a fórmula para o quadrado considera que o comprimento e a largura são iguais.
Exemplos Numéricos
- Exemplo 1: Se o comprimento (l) de um retângulo for 6 cm e a largura (w) for 8 cm, a diagonal (d) será calculada como: d = √(6² + 8²) = √(36 + 64) = √100 = 10 cm.
- Exemplo 2: Suponha um retângulo com comprimento (l) de 10 metros e largura (w) de 5 metros. A diagonal (d) é: d = √(10² + 5²) = √(100 + 25) = √125 = 11,18 metros (aproximadamente).
Interpretação Geométrica
A fórmula d = √(l² + w²) representa a aplicação do Teorema de Pitágoras para encontrar a diagonal de um retângulo. Graficamente, a diagonal forma a hipotenusa de um triângulo retângulo cujos catetos são o comprimento e a largura do retângulo.
Calculadora Online
A calculadora online de diagonal de retângulo oferece uma ferramenta prática e intuitiva para calcular a diagonal de um retângulo. Este recurso é essencial para diversas aplicações, desde cálculos geométricos até projetos de engenharia. A simplicidade e precisão da ferramenta garantem resultados confiáveis para diferentes tipos de medidas, promovendo eficiência no processo de cálculo.
Interface e Funcionalidades
A interface da calculadora online é projetada para ser clara e amigável, permitindo que usuários de todos os níveis de conhecimento interajam com a ferramenta com facilidade. A usabilidade é priorizada, visando garantir uma experiência positiva e eficiente para o cálculo da diagonal.
| Item | Descrição | Detalhes |
|---|---|---|
| Campos de Entrada | Onde o usuário insere os valores. |
|
| Campos de Saída | Onde o resultado da diagonal é exibido. |
|
| Botão de Cálculo | Botão para iniciar o cálculo da diagonal. |
|
| Botão de Limpar | Botão para limpar os campos de entrada e a saída. |
|
| Exibição de Erros | Apresentar mensagens de erro caso o usuário insira valores inválidos. |
|
| Layout | Organização visual dos elementos da interface. |
|
Cenários de Uso
A calculadora deve funcionar corretamente para diferentes entradas de dados.
| Cenário | Entrada | Saída Esperada | Descrição |
|---|---|---|---|
| Cenário 1 | Comprimento: 3, Largura: 4 | Diagonal: 5,00 cm | Cálculo de diagonal com valores inteiros. |
| Cenário 2 | Comprimento: 5.5, Largura: 2.8 | Diagonal: 6.16 cm | Cálculo com valores decimais. |
| Cenário 3 | Comprimento: -2, Largura: 4 | Mensagem de erro: “O comprimento e a largura devem ser maiores que zero.” | Tratamento de entrada inválida. |
| Cenário 4 | Comprimento: 10000, Largura: 5000 | Diagonal: 11180,34 cm | Testar com valores grandes. |
Cálculo Passo a Passo
Este tópico detalha o processo passo a passo para calcular a diagonal de um retângulo, fornecendo um guia completo e compreensível para usuários de diferentes níveis de conhecimento. Acompanhe as etapas, desde a entrada dos dados até a obtenção do resultado final, com exemplos e explicações claras.
Fluxograma
O fluxograma ilustra visualmente o processo de cálculo da diagonal de um retângulo. Ele define as etapas envolvidas, as decisões a serem tomadas e as entradas de dados necessárias. O fluxograma utiliza símbolos padronizados, facilitando a compreensão do processo.

Este fluxograma demonstra o processo completo, incluindo a entrada dos valores dos lados do retângulo (A e B), o cálculo da diagonal (D) usando a fórmula de Pitágoras, e a exibição do resultado. Observe que o símbolo de elipse representa o início e o fim do processo, os retângulos representam as ações a serem executadas, e o losango indica uma decisão a ser tomada.
As variáveis (A, B, D) são identificadas claramente em cada etapa.
Entrada de Dados na Calculadora
Para inserir os valores na calculadora, siga os passos descritos abaixo. A sequência de botões a serem pressionados é crucial para o cálculo correto.
- Passo 1: Digite o valor do lado A na calculadora. Utilize a tecla correspondente ao número. Exemplo: Se A = 3, pressione as teclas ‘3’.
- Passo 2: Pressione a tecla de elevação ao quadrado (²).
- Passo 3: Pressione a tecla ‘+’.
- Passo 4: Digite o valor do lado B na calculadora. Utilize a tecla correspondente ao número. Exemplo: Se B = 4, pressione as teclas ‘4’.
- Passo 5: Pressione a tecla de elevação ao quadrado (²).
- Passo 6: Pressione a tecla ‘=’. O resultado da soma dos quadrados de A e B será exibido.
- Passo 7: Pressione a tecla de raiz quadrada (√) para obter o valor da diagonal.
Cálculos Intermediários
Apresentamos os cálculos intermediários, demonstrando cada etapa do processo. As fórmulas matemáticas são usadas para descrever cada passo e as variáveis envolvidas são explicitadas.
| Passo | Cálculo | Variáveis |
|---|---|---|
| 1 | A² | A |
| 2 | B² | B |
| 3 | A² + B² | A, B |
| 4 | √(A² + B²) | A, B |
Exemplo: Se A = 3 e B = 4, os cálculos intermediários seriam:
- A² = 3² = 9
- B² = 4² = 16
- A² + B² = 9 + 16 = 25
- √(A² + B²) = √25 = 5
Apresentação dos Resultados
A apresentação do resultado final deve incluir a unidade de medida e o arredondamento apropriado. O resultado deve ser claro e conciso.
Apresente o resultado final com duas casas decimais e a unidade em metros.
Lista Ordenada de Passos
Os passos listados a seguir descrevem o processo de cálculo da diagonal passo a passo, para melhor compreensão e replicação do procedimento.
- Definir os valores de A e B (lados do retângulo).
- Calcular A².
- Calcular B².
- Somar A² e B².
- Calcular a raiz quadrada do resultado da soma.
- Apresentar o resultado com duas casas decimais e a unidade em metros.
Exemplos Práticos de Cálculo de Diagonal
A compreensão do cálculo da diagonal de um retângulo é fundamental em diversas áreas, desde a construção civil até a engenharia. Este tópico apresenta exemplos práticos, demonstrando a aplicação do Teorema de Pitágoras em cenários reais, com diferentes unidades de medida e contextos de aplicação.
Exemplo 1: Diagonal de um Retângulo (cm)
Este exemplo demonstra o cálculo da diagonal de um retângulo com 3 cm de comprimento e 4 cm de largura. Este tipo de cálculo é frequentemente utilizado em projetos de construção, design e fabricação.
| Comprimento | Largura | Cálculo | Resultado | Aplicações Práticas |
|---|---|---|---|---|
| 3 cm | 4 cm | Diagonal² = 3² + 4² Diagonal² = 9 + 16 Diagonal² = 25 Diagonal = √25 |
5,00 cm |
|
Exemplo 2: Diagonal de um Retângulo (m)
Neste exemplo, calculamos a diagonal de um retângulo com 5 metros de comprimento e 12 metros de largura. Este tipo de cálculo é comum em projetos de arquitetura e paisagismo.
| Comprimento | Largura | Cálculo | Resultado | Aplicações Práticas |
|---|---|---|---|---|
| 5 m | 12 m | Diagonal² = 5² + 12² Diagonal² = 25 + 144 Diagonal² = 169 Diagonal = √169 |
13,00 m |
|
Exemplo 3: Diagonal de um Retângulo (cm)
| Comprimento | Largura | Cálculo | Resultado | Aplicações Práticas |
|---|---|---|---|---|
| 8,5 cm | 6 cm | Diagonal² = 8,5² + 6² Diagonal² = 72,25 + 36 Diagonal² = 108,25 Diagonal = √108,25 |
10,41 cm |
|
Exemplo 4: Diagonal de um Retângulo (km)
| Comprimento | Largura | Cálculo | Resultado | Aplicações Práticas |
|---|---|---|---|---|
| 10 km | 25 km | Diagonal² = 10² + 25² Diagonal² = 100 + 625 Diagonal² = 725 Diagonal = √725 |
26,93 km |
|
Exemplo 5: Diagonal de um Retângulo (ft)
| Comprimento | Largura | Cálculo | Resultado | Aplicações Práticas |
|---|---|---|---|---|
| 20 ft | 15 ft | Diagonal² = 20² + 15² Diagonal² = 400 + 225 Diagonal² = 625 Diagonal = √625 |
25,00 ft |
|
Limitações e Considerações Importantes: Calculadora De Diagonal De Retângulo Online E Passo A Passo.
Esta seção detalha as limitações da Calculadora de Diagonal de Retângulo, incluindo os tipos de dados aceitos, as mensagens de erro, as unidades de medida e a precisão dos resultados. Compreender essas limitações garante que o usuário utilize a ferramenta de forma eficiente e interprete corretamente os resultados apresentados.
Tipos de Dados Aceitos
A calculadora suporta diversos tipos de dados numéricos para os cálculos. Para garantir a precisão e o bom funcionamento, é essencial que as entradas sejam consistentes com os formatos permitidos.
- Inteiros: Números inteiros positivos ou negativos, como 10, -5.
- Decimais: Números com casas decimais, como 3.14, -2.5.
- Frações: Números representados como frações, utilizando a barra (/) para separar o numerador e o denominador, como 1/2, 3/4. A calculadora também aceita frações representadas em forma decimal, como 0.5.
- Números Complexos (opcional): A calculadora pode opcionalmente lidar com números complexos, utilizando o formato a + bi, onde ‘a’ e ‘b’ são números reais e ‘i’ representa a unidade imaginária. Exemplos: 2+3i, -1-2i.
Mensagens de Erro
A calculadora exibe mensagens de erro claras e concisas para entradas inválidas, auxiliando na identificação e correção de possíveis problemas.
- Divisão por Zero: A mensagem “Erro: Divisão por zero” é exibida quando uma operação envolve a divisão por zero. Por exemplo, se o usuário tentar calcular a diagonal de um retângulo com largura zero, essa mensagem será exibida.
- Raiz Quadrada de Número Negativo: A mensagem “Erro: Raiz quadrada de número negativo” é apresentada para entradas que resultam em raiz quadrada de um número negativo, uma vez que o resultado não é um número real. Por exemplo, se o usuário inserir um valor negativo para o comprimento do lado de um retângulo e solicitar o cálculo da diagonal, essa mensagem será exibida.
Unidades de Medida
A calculadora aceita diversas unidades de medida para comprimentos. A entrada deve ser explícita e consistente para evitar erros.
- Comprimento: A calculadora aceita unidades como centímetros (cm), metros (m), milímetros (mm), etc. A entrada deve incluir a unidade, como 10 cm, 5 metros. A conversão automática entre unidades diferentes (por exemplo, cm para m) é suportada.
Precisão dos Resultados
A precisão dos resultados é um fator crucial na interpretação dos dados. A calculadora exibe os resultados com um número fixo de casas decimais para garantir clareza e evitar resultados demasiadamente longos ou confusos.
- Precisão: Os resultados são arredondados para duas casas decimais. A tolerância aceitável para arredondamento é de 0.001. Por exemplo, se o resultado for 5.004, será exibido como 5.00.
Limitações da Calculadora
A calculadora foi projetada para calcular a diagonal de um retângulo, mas possui limitações em relação à complexidade das operações.
- Operações Limitadas: A calculadora não está projetada para resolver equações complexas ou problemas envolvendo outras formas geométricas. A função principal da calculadora é calcular a diagonal de um retângulo. Ela não suporta a resolução de equações diferenciais ou outras operações matemáticas mais complexas.
Comparação com Outros Métodos
Esta seção compara a calculadora de diagonal de retângulo online com métodos alternativos, analisando a precisão, velocidade, complexidade, custo e propensão a erros de cada abordagem. A comparação abrange o cálculo manual, outras calculadoras online e softwares específicos para geometria, fornecendo insights valiosos para usuários que buscam a melhor opção para suas necessidades.
Calculadora vs. Cálculo Manual
A calculadora online demonstra significativas vantagens em relação ao cálculo manual. A precisão é muito superior, minimizando erros inerentes a cálculos feitos manualmente, especialmente quando se lida com números complexos ou cálculos repetidos. A velocidade de processamento da calculadora é consideravelmente mais rápida, economizando tempo e esforço. A complexidade do cálculo é simplificada, pois a calculadora lida com todas as etapas.
Em termos de custo, o cálculo manual implica em tempo e esforço investidos na execução dos cálculos, enquanto a calculadora online oferece uma solução instantânea. A propensão a erros é muito maior no cálculo manual, devido a possíveis falhas de atenção ou erros de digitação. Um exemplo prático é calcular a diagonal de um retângulo com lados de 3 cm e 4 cm.
Manualmente, isso pode levar alguns minutos, com potencial de erro, enquanto a calculadora fornece o resultado (5 cm) instantaneamente e com precisão.
| Critério | Cálculo Manual | Calculadora Online |
|---|---|---|
| Precisão | Variável, sujeita a erros | Alta precisão |
| Velocidade | Variável, dependendo da complexidade | Instantânea |
| Complexidade | Alta, requer compreensão das etapas | Baixa, interface simplificada |
| Custo (tempo e esforço) | Alto | Baixo |
| Propensão a Erros | Alta | Baixa |
Calculadora vs. Outras Calculadoras Online
A comparação com outras calculadoras online foca em funcionalidades, interface, velocidade, recursos adicionais e custo. A análise busca identificar as características que tornam esta calculadora uma opção vantajosa para o usuário. A interface amigável e a velocidade de processamento são fatores críticos, assim como a presença de recursos adicionais, que podem ser cruciais para certos cálculos.
- Funcionalidades: A calculadora pode oferecer funcionalidades específicas, como a apresentação dos passos do cálculo. A comparação com outras calculadoras online permite avaliar a extensão dessas funcionalidades e a sua utilidade para o usuário.
- Interface: A interface intuitiva facilita a entrada de dados e a interpretação dos resultados, o que afeta a experiência do usuário.
- Velocidade: A velocidade de processamento afeta diretamente a experiência do usuário, sendo crucial para aplicações em tempo real.
- Recursos Adicionais: Recursos extras, como gráficos ou cálculos avançados, podem ser um diferencial para a calculadora.
- Custo: A gratuidade ou o custo da calculadora são pontos importantes na escolha de uma ferramenta online.
Calculadora vs. Software Específico para Geometria
A comparação com softwares específicos para geometria considera a precisão dos resultados, as funcionalidades geométricas adicionais, a integração com outros dados e o custo do software. A calculadora pode ser uma ferramenta mais acessível e eficiente para cálculos pontuais de diagonal de retângulos, enquanto um software de geometria pode ser mais adequado para trabalhos mais complexos.
- Precisão: A calculadora deve fornecer resultados compatíveis com os softwares específicos de geometria para cálculos de diagonal.
- Funcionalidades Geométricas: A comparação deve avaliar se a calculadora possui funcionalidades além do cálculo de diagonal, como cálculo de área, perímetro ou volume.
- Integração com Outros Dados: A calculadora pode integrar dados de outros softwares para realizar cálculos mais complexos?
- Interface: A interface da calculadora deve ser intuitiva para a execução de cálculos geométricos.
- Custo: A calculadora online costuma ser gratuita, enquanto softwares específicos para geometria podem ter custos.
Aplicação em Projetos de Engenharia
A calculadora de diagonal de retângulo encontra amplas aplicações em diversos projetos de engenharia, auxiliando na resolução de problemas práticos e garantindo precisão nos cálculos. Sua simplicidade e rapidez de uso tornam-na uma ferramenta valiosa para profissionais de engenharia civil e arquitetura, otimizando o tempo e a eficiência nas tarefas diárias.A utilização da calculadora permite a obtenção rápida e precisa da diagonal de retângulos, um parâmetro fundamental em vários contextos de projeto, como em cálculos de áreas, verificação de dimensões e análise estrutural.
Aplicações em Engenharia Civil
A engenharia civil utiliza frequentemente a diagonal de retângulos em projetos de fundações, estruturas de concreto e pavimentação. Por exemplo, na construção de lajes, a diagonal de um retângulo pode auxiliar no cálculo da inclinação e do dimensionamento de vigas de apoio. A determinação precisa da diagonal é crucial para garantir a estabilidade e a segurança das estruturas. O cálculo da diagonal em planos inclinados, como rampas ou escadas, também se torna essencial para garantir a correta inclinação e segurança do projeto.
Aplicações em Arquitetura
Na arquitetura, a calculadora de diagonal de retângulo pode ser aplicada em diversos projetos, como no cálculo de áreas de ambientes, na verificação da inclinação de paredes e no dimensionamento de portas e janelas. A exatidão nos cálculos da diagonal de retângulos é fundamental para garantir a proporcionalidade e a estética dos projetos arquitetônicos. Por exemplo, o cálculo da diagonal de uma sala retangular auxilia na determinação da área total, necessária para o cálculo de materiais de construção.
Utilização em Desenhos Técnicos
A calculadora de diagonal de retângulo auxilia significativamente em desenhos técnicos. Ao possibilitar a rápida e precisa determinação da diagonal, o profissional pode representar com precisão os objetos nos desenhos, facilitando a visualização e o entendimento do projeto. A representação gráfica precisa dos objetos e estruturas é crucial para a comunicação eficaz entre os membros da equipe e para a execução do projeto.
A diagonal também pode auxiliar na representação de elementos inclinados, como rampas e telhados.
Cálculo de Área
A calculadora pode auxiliar no cálculo da área de um retângulo, pois conhecendo-se os lados, é possível calcular a diagonal e, posteriormente, a área. A área é calculada multiplicando-se a medida da base pela medida da altura. Conhecendo-se a diagonal e um dos lados, pode-se encontrar o outro lado e, assim, a área. Este cálculo é importante para o dimensionamento de espaços e a estimação de materiais de construção.
Em resumo, a calculadora simplifica o processo de cálculo da área, proporcionando maior precisão e agilidade.
Aplicação em Projetos de Design
A calculadora de diagonal de retângulo oferece ferramentas valiosas para designers, permitindo a criação precisa e eficiente de layouts, com cálculos rápidos e precisos de proporções. Sua aplicação vai além dos cálculos básicos, auxiliando na organização espacial e na determinação de medidas ideais para diversos tipos de projetos.A utilização da calculadora em projetos de design gráfico e de interiores proporciona um processo mais organizado e assertivo, permitindo que os profissionais se concentrem em aspectos estéticos e criativos, sem se preocupar com cálculos complexos.
Com a automatização de cálculos de diagonais, a produtividade e a precisão são aprimoradas, garantindo maior confiabilidade nas etapas de concepção e execução do projeto.
Aplicações em Design Gráfico
A calculadora de diagonal de retângulos é essencial para a criação de layouts em design gráfico, permitindo a determinação de proporções e posições de elementos visuais. Por exemplo, na composição de um logotipo ou banner, a compreensão da diagonal de um retângulo auxilia na definição de ângulos, direcionamento visual e harmonia estética. A precisão em calcular a diagonal permite posicionar elementos com precisão, evitando distorções ou desalinhamentos que prejudicariam a estética da peça gráfica.
A possibilidade de realizar esses cálculos rapidamente permite a iteração e experimentação de diferentes layouts.
Aplicações em Design de Interiores
A calculadora de diagonal de retângulos pode ser utilizada para determinar a medida ideal de objetos e espaços em projetos de design de interiores. Por exemplo, ao projetar um quarto, o cálculo da diagonal de um piso retangular pode ajudar a definir a disposição dos móveis, garantindo que as peças se encaixem perfeitamente e proporcionando um ambiente harmônico. O cálculo preciso da diagonal é fundamental para a organização e aproveitamento de espaços, especialmente em ambientes com layouts complexos ou necessidades específicas.
Utilização na Criação de Layouts
A calculadora facilita a criação de layouts, permitindo que os designers visualizem e dimensionem corretamente os elementos gráficos em uma composição. Ao calcular a diagonal de um retângulo, é possível posicionar objetos de maneira estratégica, otimizando o espaço disponível e garantindo a harmonia visual. Essa ferramenta é útil para diferentes tipos de layouts, desde a criação de um site ou revista, até a organização de uma apresentação ou material promocional.
Por meio de cálculos precisos, os designers podem construir layouts mais eficientes e atraentes.
Utilização em Cálculos de Proporções
A calculadora de diagonal de retângulos é uma ferramenta valiosa para determinar proporções em projetos de design. Por exemplo, na criação de um cartaz ou flyer, a proporção entre os elementos gráficos pode ser otimizada para maximizar a comunicação e atrair a atenção do público. A ferramenta permite a análise e o ajuste das proporções, assegurando a criação de peças visuais esteticamente agradáveis e eficientes.
A capacidade de realizar esses cálculos de proporções garante um design equilibrado e impactante.
Formatação da Informação
A formatação clara e concisa dos dados é crucial para a compreensão e utilização da calculadora de diagonal de retângulo. A apresentação organizada dos exemplos, passos do cálculo e aplicações em projetos torna a ferramenta mais amigável e eficiente. Esta seção detalha a estruturação da informação por meio de tabelas responsivas e citações, maximizando a usabilidade e a compreensão.
Exemplos Práticos de Cálculo de Diagonal, Calculadora de diagonal de retângulo online e passo a passo.
A apresentação dos exemplos de cálculo de diagonal em uma tabela responsiva permite uma visualização clara e eficiente dos dados. A estrutura tabular permite comparar diferentes situações de forma organizada e facilita a compreensão dos resultados.
| Comprimento (cm) | Largura (cm) | Diagonal (cm) | Observações |
|---|---|---|---|
| 10 | 5 | 11.18 | Exemplo básico. |
| 15 | 8 | 17.00 | Retângulo maior. |
| 20 | 12 | 23.32 | Retângulo ainda maior. |
| 30 | 15 | 33.54 | Exemplo com medidas maiores. |
Etapas do Cálculo Passo a Passo
A organização das etapas de cálculo em uma tabela responsiva facilita a compreensão e a verificação dos passos envolvidos no processo. A tabela, com sua estrutura de colunas, torna mais claro cada passo intermediário, permitindo a verificação do resultado em cada etapa.
| Etapa | Descrição | Cálculo | Resultado |
|---|---|---|---|
| 1 | Identificar o comprimento e a largura do retângulo. | Lembre-se das medidas do retângulo. | Ex: Comprimento = 10cm, Largura = 5cm |
| 2 | Elevar ao quadrado o comprimento e a largura. | c² = 10² = 100, l² = 5² = 25 | c² = 100, l² = 25 |
| 3 | Somar os valores obtidos na etapa anterior. | c² + l² = 100 + 25 = 125 | 125 |
| 4 | Calcular a raiz quadrada do resultado da etapa anterior. | √125 ≈ 11.18 | 11.18 cm |
Aplicações em Projetos
A organização das aplicações em uma tabela responsiva demonstra a versatilidade da calculadora de diagonal de retângulo em diferentes contextos. As diferentes aplicações destacam o amplo espectro de utilização da ferramenta.
| Projeto | Descrição | Utilização da Diagonal | Exemplo |
|---|---|---|---|
| Engenharia Civil | Cálculo de vigas, lajes e estruturas. | Determinação do comprimento de materiais e espaçamento de elementos estruturais. | Dimensionamento de vigas para suportar cargas. |
| Design de Interiores | Dimensionamento de móveis e objetos. | Verificação do encaixe de peças e otimização de espaços. | Posicionamento de mesas e sofás em um ambiente. |
| Construção | Cálculo de materiais de construção. | Determinação da quantidade de madeira, tijolos ou outros materiais. | Cálculo de área de um terreno retangular. |
| Projetos de Paisagismo | Dimensionamento de canteiros e caminhos. | Definição de formas e tamanhos de áreas verdes. | Layout de um jardim retangular. |
Ilustrações e Visualizações
As ilustrações são ferramentas valiosas para a compreensão de conceitos matemáticos, como o cálculo da diagonal de um retângulo. Imagens claras e bem elaboradas facilitam a visualização das relações geométricas e auxiliam na assimilação dos passos envolvidos no processo. Acompanhar as ilustrações com descrições detalhadas contribui para a compreensão aprofundada dos conceitos.
Imagem Ilustrativa de um Retângulo com sua Diagonal
Imagine um retângulo ABCD. Uma linha reta traçada a partir do vértice A até o vértice C, representando a diagonal AC, é ilustrada. A figura demonstra a relação entre os lados do retângulo (comprimento e largura) e a diagonal, formando um triângulo retângulo. Esta visualização é fundamental para compreender a aplicação do Teorema de Pitágoras para calcular a diagonal.
Imagem Ilustrativa Comparando Diferentes Retângulos com suas Diagonais
Uma série de retângulos com diferentes comprimentos e larguras são apresentados, cada um com sua diagonal traçada. Esta comparação visual mostra como a diagonal varia em relação às dimensões do retângulo. Por exemplo, um retângulo maior com lados proporcionais terá uma diagonal maior em comparação a um retângulo menor com lados proporcionais. A imagem reforça a relação direta entre as dimensões do retângulo e o comprimento de sua diagonal.
Imagem Ilustrativa de Como Usar a Calculadora Online
Uma imagem ilustra a interface de uma calculadora online para o cálculo da diagonal de um retângulo. São apresentados campos para a entrada dos valores do comprimento e da largura do retângulo. A calculadora exibe os passos do cálculo e o resultado final da diagonal, com destaque nos campos de entrada e no resultado. A imagem demonstra a facilidade de utilização da ferramenta online.
Imagem Ilustrativa de uma Aplicação em um Projeto Arquitetônico
Uma planta baixa de um projeto arquitetônico é apresentada. Sobre ela, uma diagonal é traçada para representar um elemento estrutural, como uma viga ou uma parede, que atravessa o espaço. A diagonal, calculada utilizando a ferramenta online, auxilia no dimensionamento e na precisão do projeto, assegurando a estabilidade e a funcionalidade da estrutura. A imagem ilustra como o cálculo da diagonal de um retângulo é crucial em projetos de engenharia e arquitetura.
Diferentes Formatos de Apresentação
A calculadora de diagonal de retângulo online e passo a passo pode ser apresentada em diferentes formatos para atender às necessidades e preferências dos usuários. A escolha do formato adequado depende do contexto de uso, seja para estudantes, engenheiros, designers ou qualquer pessoa que precise calcular diagonais. A clareza e a organização da informação são cruciais para uma experiência de usuário positiva.
Cálculo de Diagonais em Diferentes Contextos
A aplicação do cálculo de diagonais de retângulos varia consideravelmente dependendo do contexto. Em projetos de engenharia, a precisão é fundamental para garantir a segurança e a eficácia das estruturas. Já em projetos de design, a diagonal pode ser usada para determinar proporções e ângulos estéticos. Entender a necessidade específica do usuário permite a escolha de um formato de apresentação adequado, que inclua desde a formulação matemática até os exemplos práticos.
Vantagens de Utilizar uma Calculadora Online
O uso de uma calculadora online para o cálculo de diagonais oferece inúmeras vantagens. A principal vantagem é a praticidade, pois elimina a necessidade de cálculos manuais, reduzindo a probabilidade de erros. Além disso, a calculadora online permite que os usuários concentrem seus esforços na análise dos resultados, sem se preocupar com os cálculos intermediários. A rapidez e a confiabilidade dos resultados são outras vantagens significativas, especialmente em situações que exigem agilidade e precisão.
A facilidade de acesso, independente de localização geográfica, também contribui para a universalização do uso da ferramenta.
Importância da Precisão nos Cálculos
A precisão nos cálculos de diagonais é essencial em diversas aplicações, particularmente em contextos que envolvem estruturas ou medidas críticas. A falta de precisão pode levar a erros significativos, com implicações que vão desde a estética em projetos de design até a segurança em projetos de engenharia. Por exemplo, uma pequena diferença em uma medida de diagonal em uma estrutura pode comprometer a estabilidade do projeto.
O uso de uma calculadora online com resultados detalhados pode auxiliar na compreensão dos passos intermediários e na verificação da precisão. Um resultado preciso é crucial para garantir a eficácia e segurança do projeto, independente do campo de aplicação.
Exemplos de Dados de Entrada e Saída
Para ilustrar o funcionamento da calculadora de diagonal de retângulo, apresentamos a seguir diversos exemplos práticos. Cada exemplo inclui o comprimento, a largura e o resultado da diagonal calculada, permitindo que o usuário compreenda melhor o processo e valide os resultados obtidos pela ferramenta online.
Exemplos com Valores Inteiros
Os exemplos a seguir utilizam valores inteiros para o comprimento e a largura do retângulo, mostrando a aplicação da fórmula em situações simples.
- Exemplo 1: Comprimento = 3, Largura = 4. A diagonal é calculada como √(3² + 4²) = √25 = 5.
- Exemplo 2: Comprimento = 6, Largura = 8. A diagonal é calculada como √(6² + 8²) = √100 = 10.
- Exemplo 3: Comprimento = 12, Largura = 5. A diagonal é calculada como √(12² + 5²) = √169 = 13.
Exemplos com Valores Decimais
Nesta seção, demonstramos a aplicação da fórmula com valores decimais para o comprimento e a largura.
- Exemplo 4: Comprimento = 5,5, Largura = 8,2. A diagonal é calculada como √(5,5² + 8,2²) ≈ √88,09 + 67,24 = √155,33 ≈ 12,46.
- Exemplo 5: Comprimento = 10.2, Largura = 12.6. A diagonal é calculada como √(10.2² + 12.6²) ≈ √104.04 + 158.76 = √262.8 ≈ 16.21.
Exemplos com Valores Fracionários
Apresentamos a seguir exemplos com valores fracionários para o comprimento e a largura, mostrando como a fórmula se aplica a esses casos.
- Exemplo 6: Comprimento = 3/2, Largura = 4/3. A diagonal é calculada como √((3/2)² + (4/3)²) = √(9/4 + 16/9) = √(81/36 + 64/36) = √(145/36) ≈ √4.0277 ≈ 2.007.
- Exemplo 7: Comprimento = 5/4, Largura = 7/2. A diagonal é calculada como √((5/4)² + (7/2)²) = √(25/16 + 49/4) = √(25/16 + 196/16) = √(221/16) ≈ √13.8125 ≈ 3.71.
Tabela Resumida
A tabela a seguir resume os exemplos apresentados, facilitando a compreensão e a comparação dos resultados.
| Comprimento | Largura | Diagonal |
|---|---|---|
| 3 | 4 | 5 |
| 6 | 8 | 10 |
| 5.5 | 8.2 | 12.46 (aproximado) |
| 10.2 | 12.6 | 16.21 (aproximado) |
| 3/2 | 4/3 | 2.007 (aproximado) |
| 5/4 | 7/2 | 3.71 (aproximado) |
Em resumo, a Calculadora de diagonal de retângulo online e passo a passo. é uma ferramenta essencial para diversas áreas, facilitando cálculos de diagonais com precisão e rapidez. Sua interface amigável e exemplos práticos tornam o uso intuitivo e acessível para qualquer usuário, eliminando a necessidade de cálculos manuais complexos. A ferramenta demonstra sua aplicabilidade em cenários reais, como projetos de móveis, design de interiores e engenharia, destacando-se como uma solução prática e eficaz.
Qual a precisão dos cálculos da calculadora?
A calculadora arredonda os resultados para duas casas decimais, garantindo uma precisão adequada para a maioria das aplicações práticas.
A calculadora suporta diferentes unidades de medida?
Sim, a calculadora permite a entrada de valores em diversas unidades, como centímetros, metros, milímetros, entre outras. É importante manter a consistência nas unidades de medida para obter resultados corretos.
O que fazer se eu inserir um valor inválido na calculadora?
A calculadora exibirá uma mensagem de erro clara e concisa caso o usuário insira valores inválidos, como valores negativos ou não numéricos, informando que o comprimento e a largura devem ser maiores que zero.
Como a calculadora difere de outros métodos de cálculo?
A calculadora oferece praticidade e rapidez, evitando erros comuns em cálculos manuais, além de ser acessível a qualquer pessoa, mesmo sem conhecimentos profundos de geometria. O cálculo manual pode ser mais trabalhoso e propenso a erros, enquanto a calculadora fornece resultados precisos e instantâneos.