Diferença entre calcular a diagonal de um retângulo e um quadrado. Este tópico explora as nuances matemáticas envolvidas em determinar o comprimento da diagonal desses dois quadriláteros. Enquanto ambos utilizam o Teorema de Pitágoras, as fórmulas e os processos de cálculo apresentam diferenças importantes, que serão detalhadas neste estudo.
A compreensão dessas diferenças é fundamental para a resolução de problemas geométricos e para a aplicação prática em diversos contextos, desde a arquitetura até a engenharia. Vamos desvendar as particularidades de cada caso e identificar as relações entre os lados e a diagonal.
Introdução à Geometria Plana
A Geometria Plana é um ramo da matemática que estuda as figuras geométricas bidimensionais, como retângulos e quadrados. Compreender as propriedades dessas figuras é fundamental para diversas áreas, desde a arquitetura e engenharia até a arte e design. Neste tópico, exploraremos os conceitos de retângulo e quadrado, suas propriedades geométricas e as características que os distinguem.
Conceitos de Retângulo e Quadrado
Retângulos e quadrados são quadriláteros, ou seja, polígonos com quatro lados. Um retângulo é um quadrilátero que possui quatro ângulos retos (90°) e lados opostos congruentes (iguais). Um quadrado é um quadrilátero especial, pois além de ter quatro ângulos retos, possui todos os quatro lados congruentes. Essa característica adicional o diferencia do retângulo.
Propriedades Geométricas de Retângulos e Quadrados
Os retângulos e quadrados compartilham algumas propriedades geométricas, mas também possuem características únicas. As propriedades comuns incluem:
- Possuem quatro lados;
- Todos os ângulos internos são retos (90°);
- Os lados opostos são paralelos;
- Os lados opostos são congruentes.
As propriedades específicas de cada figura são:
- Retângulo: Os lados opostos são congruentes. As diagonais são congruentes e se cruzam em seus pontos médios. Um retângulo pode ser visto em uma porta ou janela retangular.
- Quadrado: Todos os quatro lados são congruentes. As diagonais são congruentes, se cruzam em seus pontos médios e formam ângulos retos (90°) entre si. Um quadrado é a forma básica de muitos pisos ou blocos.
Comparação entre Retângulos e Quadrados
A principal diferença entre retângulos e quadrados reside na congruência dos lados. Enquanto os retângulos possuem apenas lados opostos congruentes, os quadrados possuem todos os quatro lados congruentes. Essa característica adicional confere ao quadrado simetria e proporções específicas, o que o diferencia do retângulo.
Tabela Comparativa de Propriedades
A tabela a seguir resume as propriedades dos retângulos e quadrados, permitindo uma comparação direta.
| Propriedade | Retângulo | Quadrado |
|---|---|---|
| Lados | Lados opostos congruentes | Todos os quatro lados congruentes |
| Ângulos | Quatro ângulos retos (90°) | Quatro ângulos retos (90°) |
| Diagonais | Congruentes e se cruzam em seus pontos médios | Congruentes, se cruzam em seus pontos médios e formam ângulos retos (90°) |
| Simetria | Simetria em relação a dois eixos | Simetria em relação a quatro eixos |
Cálculo da Diagonal de um Retângulo
Para determinar a distância entre dois vértices opostos de um retângulo, calcula-se a sua diagonal. Este cálculo é fundamental em diversas aplicações, desde projetos de engenharia até problemas cotidianos, como determinar o comprimento de uma escada apoiada em uma parede. A compreensão da fórmula e sua aplicação prática é crucial para a resolução de tais problemas.
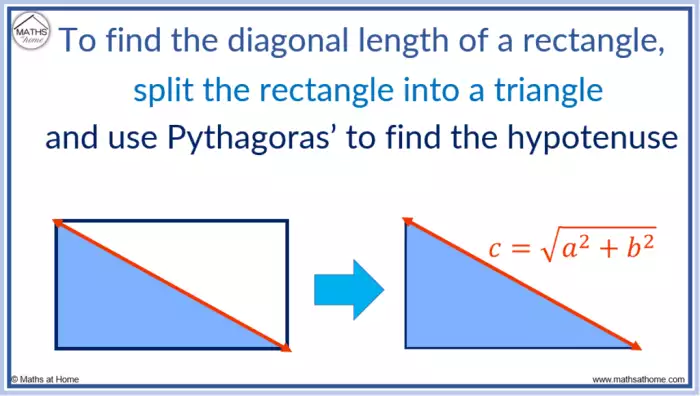
Fórmula da Diagonal de um Retângulo
A diagonal de um retângulo pode ser calculada utilizando o Teorema de Pitágoras. Este teorema estabelece uma relação entre os lados de um triângulo retângulo, permitindo determinar o comprimento da hipotenusa (a diagonal do retângulo) conhecendo os comprimentos dos catetos (os lados do retângulo).
d = √(a² + b²)
onde:* d representa o comprimento da diagonal;
- a representa a medida do comprimento do retângulo;
- b representa a medida da largura do retângulo.
Exemplos de Cálculo da Diagonal
Para ilustrar a aplicação prática da fórmula, seguem exemplos numéricos detalhados:
- Exemplo 1: Um retângulo possui um comprimento de 6 cm e uma largura de 8 cm. Determine o comprimento da diagonal.
- Solução:
- Identifique os valores conhecidos: a = 6 cm e b = 8 cm.
- Substitua os valores na fórmula: d = √(6² + 8²) = √(36 + 64) = √100.
- Calcule a raiz quadrada: d = 10 cm.
- Conclusão: A diagonal do retângulo mede 10 cm.
- Exemplo 2: Um retângulo tem um comprimento de 12 metros e uma largura de 5 metros. Calcule o comprimento da diagonal.
- Solução:
- Identifique os valores conhecidos: a = 12 m e b = 5 m.
- Substitua os valores na fórmula: d = √(12² + 5²) = √(144 + 25) = √169.
- Calcule a raiz quadrada: d = 13 m.
- Conclusão: A diagonal do retângulo mede 13 metros.
Cálculo da Diagonal de um Quadrado
O cálculo da diagonal de um quadrado é um conceito fundamental na geometria plana, com aplicações em diversas áreas, desde a engenharia até a arte. Compreender essa fórmula permite a resolução de problemas que envolvem a medição de espaços e a construção de figuras geométricas precisas.
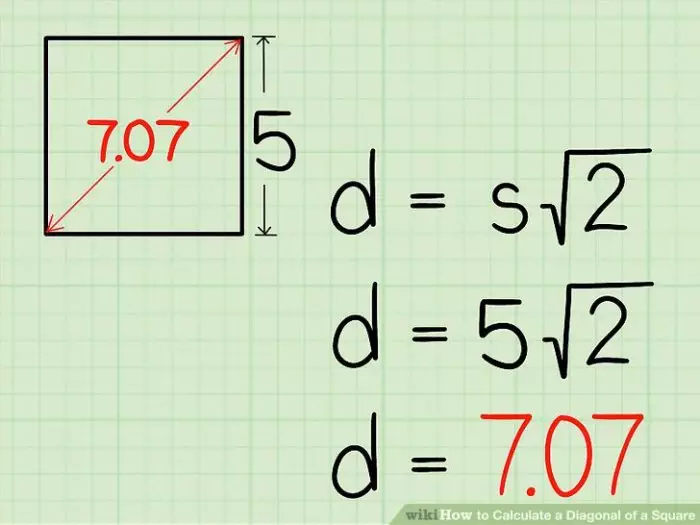
Fórmula da Diagonal de um Quadrado
A fórmula para calcular a diagonal de um quadrado relaciona a medida de seus lados com a medida da diagonal. A diagonal de um quadrado divide o quadrado em dois triângulos retângulos isósceles congruentes. Aplicando o Teorema de Pitágoras, podemos estabelecer a relação entre os lados e a diagonal.
d = l√2
Onde:* d representa a medida da diagonal;
l representa a medida de cada lado do quadrado.
Comparação com a Diagonal de um Retângulo
A fórmula para calcular a diagonal de um retângulo é diferente da fórmula para um quadrado. Para um retângulo, a diagonal é calculada usando o Teorema de Pitágoras, considerando os lados como catetos.
d = √(a² + b²)
Onde:* d representa a medida da diagonal;
a e b representam as medidas dos lados do retângulo.
A principal diferença reside na relação entre os lados e a diagonal. No quadrado, os lados possuem a mesma medida (l), o que simplifica a fórmula para d = l√2. No retângulo, os lados possuem medidas diferentes (a e b), o que leva à fórmula mais complexa.
Relação entre Lados e Diagonal em um Quadrado
A relação entre os lados e a diagonal de um quadrado é fundamental para a compreensão da geometria. A diagonal de um quadrado é sempre maior que qualquer um dos seus lados, e a relação entre eles é sempre a mesma, √2 vezes maior. Isso é consequência direta do Teorema de Pitágoras aplicado a um triângulo retângulo isósceles formado pela diagonal e dois lados do quadrado.
Exemplo Numérico
Considere um quadrado com lados medindo 5 cm. Para calcular a diagonal, aplicamos a fórmula:d = l√2d = 5√2d ≈ 7,07 cmPortanto, a diagonal do quadrado com lados de 5 cm mede aproximadamente 7,07 cm.
Relação entre Lados e Diagonal
A relação entre os lados e a diagonal de um retângulo ou quadrado é fundamental para determinar o comprimento da diagonal, dado o tamanho dos lados. Compreender essa relação permite calcular a diagonal com precisão e aplicar esse conhecimento em diversos problemas geométricos e práticos.
Influência dos Lados no Comprimento da Diagonal de um Retângulo
O comprimento da diagonal de um retângulo depende diretamente dos comprimentos de seus lados. A relação entre os lados e a diagonal de um retângulo é descrita pelo Teorema de Pitágoras. Dados os lados a e b de um retângulo, a diagonal d pode ser calculada pela seguinte fórmula:
d = √(a² + b²)
Observamos que, à medida que os lados a e b aumentam, o valor da diagonal d também aumenta. A variação não é linear, mas sim proporcional à raiz quadrada da soma dos quadrados dos lados.
Relação entre Lados e Diagonal de um Quadrado
No caso específico de um quadrado, onde os quatro lados possuem o mesmo comprimento ( l), a fórmula simplifica. A diagonal d de um quadrado é calculada como:
d = l√2
Essa fórmula demonstra que a diagonal de um quadrado é sempre proporcional ao seu lado, multiplicado por √2. A relação é direta e constante, pois o fator √2 é sempre o mesmo, independentemente do tamanho do lado.
Exemplos de Valores para Lados e Diagonais
| Lado (a) | Lado (b) | Diagonal (d) |
|---|---|---|
| 3 cm | 4 cm | 5 cm |
| 5 cm | 12 cm | 13 cm |
| 6 cm | 8 cm | 10 cm |
| 7 cm | 24 cm | 25 cm |
| 10 cm | 10 cm | 14.14 cm |
A tabela ilustra exemplos de retângulos com diferentes lados e suas respectivas diagonais. É possível observar a variação dos valores, de acordo com o aumento dos lados. Note que no último exemplo, o quadrado tem lados iguais, e a diagonal é calculada usando a fórmula específica para o quadrado.
Variação do Comprimento da Diagonal em Função da Alteração dos Lados
A variação do comprimento da diagonal em função da alteração dos lados é diretamente proporcional à alteração dos lados. Se os lados do retângulo ou do quadrado forem duplicados, a diagonal será multiplicada por √2 (no caso do quadrado) ou por um valor maior que a raiz quadrada da soma dos quadrados dos lados duplicados (no caso do retângulo). A alteração é mais acentuada em retângulos com lados muito diferentes.
Comparação entre os Cálculos
A comparação dos métodos de cálculo da diagonal em retângulos e quadrados revela importantes semelhanças e diferenças, que permitem uma compreensão mais aprofundada da geometria. Compreender essas distinções facilita a aplicação correta das fórmulas em diferentes contextos.A principal diferença reside na forma como a relação entre os lados e a diagonal é estabelecida. Enquanto em ambos os casos se utiliza o Teorema de Pitágoras, a presença de lados iguais no quadrado simplifica o cálculo, o que não acontece no retângulo.
Comparação das Fórmulas e Passos
Para elucidar as diferenças e semelhanças, apresentamos uma tabela comparativa.
| Característica | Retângulo | Quadrado |
|---|---|---|
| Fórmula da Diagonal |
, onde ‘a’ e ‘b’ são os lados do retângulo. |
, onde ‘l’ é o lado do quadrado. |
| Passos para o Cálculo | 1. Identificar os comprimentos dos lados ‘a’ e ‘b’. 2. Substituir os valores de ‘a’ e ‘b’ na fórmula. 3. Calcular a soma dos quadrados dos lados. 4. Calcular a raiz quadrada do resultado. |
1. Identificar o comprimento do lado ‘l’. 2. Substituir o valor de ‘l’ na fórmula simplificada. 3. Calcular o resultado. |
| Propriedades Importantes | Os lados ‘a’ e ‘b’ possuem comprimentos diferentes. O retângulo possui ângulos retos. |
Os lados ‘l’ possuem o mesmo comprimento. O quadrado possui ângulos retos e lados congruentes. |
A tabela demonstra como a fórmula para o quadrado se torna mais simples devido à igualdade dos lados, resultando em uma expressão mais concisa.
Propriedades que Diferenciam os Cálculos
As propriedades geométricas dos retângulos e quadrados influenciam diretamente a forma como a diagonal é calculada. No retângulo, a diagonal relaciona dois lados diferentes, enquanto no quadrado, a diagonal relaciona dois lados iguais. Essa diferença fundamental afeta a simplificação da fórmula e o processo de cálculo.
Aplicações Práticas
O cálculo da diagonal de um retângulo ou quadrado, embora pareça um conceito abstrato da geometria, possui inúmeras aplicações práticas em diversos campos. Desde a construção civil até a arte gráfica, a compreensão desse cálculo é fundamental para a precisão e a eficiência em diferentes tarefas. Neste tópico, serão apresentados exemplos práticos, detalhando situações em que a diagonal é crucial e problematizando sua utilização em diferentes contextos.Compreender a relação entre os lados e a diagonal é fundamental para diversas aplicações práticas.
A diagonal, que conecta dois vértices opostos de um retângulo ou quadrado, representa a distância mais curta entre esses pontos, o que a torna crucial em cálculos envolvendo distâncias, áreas e volumes.
Construções
A diagonal é fundamental na construção civil, auxiliando na determinação de comprimentos, ângulos e na verificação da perpendicularidade entre paredes e estruturas. Em obras de alvenaria, por exemplo, a diagonal de um tijolo ou bloco é utilizada para garantir que as paredes estejam corretamente alinhadas e retas. O uso de instrumentos como o nível e a régua é crucial para determinar se as paredes formam ângulos retos.
- Na construção de um muro de alvenaria, é crucial garantir que os tijolos ou blocos estejam dispostos em ângulos retos. A medição da diagonal de um retângulo formado por dois tijolos adjacentes pode verificar se o ângulo é reto, evitando desníveis e problemas estruturais.
- Na construção de rampas, a diagonal de um retângulo ou triângulo formado pela rampa e o terreno determina o comprimento necessário da rampa e o seu ângulo de inclinação. Isso é fundamental para garantir a acessibilidade e segurança da rampa.
- Na construção de estruturas como telhados, a diagonal de um triângulo formado pelos dois lados do telhado é utilizada para determinar o comprimento das vigas e a inclinação do telhado. Um cálculo preciso é essencial para garantir a estabilidade da estrutura.
Artes Gráficas
Nas artes gráficas, a diagonal é usada para criar efeitos visuais e para garantir a precisão em layouts. Por exemplo, em design gráfico, a diagonal pode indicar movimento, dinamismo ou direção. Também é fundamental para garantir que as imagens e elementos estejam alinhados corretamente em uma página.
- Na criação de um logotipo, a inclinação de uma linha diagonal pode transmitir diferentes sensações e significados, desde a modernidade até a tradição.
- Na diagramação de um livro ou revista, a diagonal é utilizada para posicionar textos e imagens de forma estética e eficiente.
- A diagonal de um retângulo na composição de uma imagem fotográfica pode ajudar a guiar o olhar do espectador.
Problemas de Aplicação
Apresentam-se alguns problemas práticos que demonstram a aplicação do cálculo da diagonal em diferentes contextos.
- Um pintor precisa cobrir uma parede retangular com 3 metros de largura e 4 metros de altura. Qual o comprimento mínimo de uma escada que ele precisa para alcançar o canto superior da parede?
A diagonal de um retângulo com lados a e b é calculada por √(a² + b²).
A solução envolve a aplicação da fórmula da diagonal para um retângulo, resultando em uma escada de 5 metros. - Um carpinteiro precisa construir uma estrutura em forma de quadrado com lados de 2,5 metros. Qual é a medida da diagonal da estrutura?
A diagonal de um quadrado com lado a é calculada por a√2.
Aplicando a fórmula da diagonal para um quadrado, a diagonal terá 2,5√2 metros, aproximadamente 3,54 metros.
Teorema de Pitágoras
O Teorema de Pitágoras é um princípio fundamental da geometria que estabelece uma relação crucial entre os lados de um triângulo retângulo. Sua importância reside na capacidade de determinar a medida de um lado desconhecido quando conhecemos os outros dois, o que se torna fundamental em diversos cálculos geométricos, incluindo a determinação da diagonal de um retângulo e de um quadrado.O Teorema de Pitágoras estabelece que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os dois lados que formam o ângulo reto).
Esta relação permite deduzir fórmulas para o cálculo da diagonal em figuras geométricas como retângulos e quadrados.
Relação com o Cálculo da Diagonal
O cálculo da diagonal de um retângulo ou de um quadrado pode ser deduzido diretamente a partir do Teorema de Pitágoras. Imagine um retângulo ou um quadrado. Ao traçar a diagonal, criamos um triângulo retângulo, onde a diagonal é a hipotenusa e os lados do retângulo ou do quadrado são os catetos.
Demonstração do Teorema de Pitágoras
A demonstração geométrica do Teorema de Pitágoras envolve a decomposição de quadrados construídos sobre os lados do triângulo retângulo. Existem diversas demonstrações, sendo uma delas a seguinte:
Considerando um quadrado de lado (a + b) e dividindo-o em quatro triângulos retângulos congruentes ao original, mais um quadrado de lado c. A área total do quadrado maior é (a + b)2. A área do quadrado menor é c 2. A soma das áreas dos quatro triângulos retângulos é igual a 2ab. Assim, temos a equação: (a + b) 2 = c 2 + 4
- (1/2
- a
- b) = c 2 + 2ab. Simplificando, obtemos a relação fundamental a 2 + b 2 = c 2.
Aplicação em Retângulos
Para um retângulo com lados a e b, a diagonal (d) pode ser calculada usando a fórmula derivada do Teorema de Pitágoras: d 2 = a 2 + b 2. Portanto, d = √(a 2 + b 2).
Aplicação em Quadrados
Em um quadrado com lado a, a diagonal (d) é calculada da mesma forma, porém, como os lados são iguais, a fórmula se simplifica para: d = √(a 2 + a 2) = √(2a 2) = a√2.
Exemplo de Retângulo
Considere um retângulo com lados medindo 3 cm e 4 cm. Aplicando a fórmula, a diagonal (d) é calculada como: d = √(3 2 + 4 2) = √(9 + 16) = √25 = 5 cm.
Exemplo de Quadrado
Um quadrado com lado de 5 cm terá uma diagonal de: d = 5√2 cm, aproximadamente 7,07 cm.
Imagens Ilustrativas
Para uma melhor compreensão da relação entre os lados e a diagonal de um retângulo e um quadrado, as imagens são ferramentas valiosas. A visualização geométrica facilita a assimilação dos conceitos e a aplicação do Teorema de Pitágoras. As representações visuais demonstram claramente as proporções e as relações matemáticas envolvidas.As imagens a seguir ilustram as diagonais de retângulos e quadrados com diferentes dimensões, mostrando como o comprimento da diagonal se relaciona com os comprimentos dos lados.
Cada exemplo destaca a aplicação prática do Teorema de Pitágoras.
Exemplos de Retângulos
As figuras demonstram retângulos com lados de comprimentos distintos, mas com a mesma diagonal.
- Retângulo 1: Um retângulo com lados medindo 3 cm e 4 cm. A diagonal, calculada pelo Teorema de Pitágoras (√(3² + 4²)), mede 5 cm. A imagem mostrará um retângulo com as medidas dos lados e a diagonal, com a diagonal traçada a partir de um vértice até o vértice oposto. Essa imagem ajudará a visualizar a relação entre os lados e a diagonal, demonstrando que a diagonal é a hipotenusa de um triângulo retângulo cujos catetos são os lados do retângulo.
- Retângulo 2: Um retângulo com lados medindo 6 cm e 8 cm. A diagonal, calculada por √(6² + 8²), também mede 10 cm. Similarmente ao exemplo anterior, a imagem apresentará as medidas dos lados e a diagonal, mostrando a diagonal como a hipotenusa do triângulo retângulo formado pelos lados do retângulo. A visualização permite a compreensão de que, apesar de os lados terem valores diferentes, a diagonal mantém um valor constante em relação aos seus lados.
Exemplos de Quadrados
Os exemplos de quadrados demonstram a relação entre os lados e a diagonal de um quadrado.
- Quadrado 1: Um quadrado com lados medindo 5 cm. A diagonal, calculada por √(5² + 5²), mede 5√2 cm, aproximadamente 7,07 cm. A imagem do quadrado mostrará as medidas dos lados e a diagonal. A diagonal será traçada a partir de um vértice até o vértice oposto, evidenciando a relação entre os lados e a diagonal do quadrado, onde a diagonal é a hipotenusa de um triângulo retângulo isósceles cujos catetos são os lados do quadrado.
- Quadrado 2: Um quadrado com lados medindo 10 cm. A diagonal, calculada por √(10² + 10²), mede 10√2 cm, aproximadamente 14,14 cm. A imagem apresentará o quadrado com suas medidas e a diagonal. Essa representação ajuda a compreender como a diagonal se relaciona com os lados de um quadrado, demonstrando a constante proporção entre os lados e a diagonal. O triângulo formado pela diagonal e os lados do quadrado é um triângulo retângulo isósceles.
Detalhes das Imagens
As imagens devem apresentar claramente:
- Os comprimentos dos lados do retângulo ou quadrado.
- A diagonal traçada no retângulo ou quadrado.
- A representação do triângulo retângulo formado pela diagonal e os lados do retângulo ou quadrado.
- As medidas da diagonal, calculada usando o Teorema de Pitágoras.
As imagens auxiliam na compreensão do conceito ao:
- Permitir a visualização da relação entre os lados e a diagonal.
- Demonstrar a aplicação do Teorema de Pitágoras na geometria.
- Tornar mais intuitivo o cálculo da diagonal.
Diferenças Conceituais: Diferença Entre Calcular A Diagonal De Um Retângulo E Um Quadrado.
Os retângulos e os quadrados, apesar de ambos serem quadriláteros, possuem características distintas que impactam diretamente nos cálculos de suas diagonais. Compreender essas diferenças conceituais é fundamental para aplicar corretamente as fórmulas e interpretar os resultados. A precisão em distinguir um retângulo de um quadrado é essencial para a resolução de problemas geométricos e para a aplicação prática desses conceitos em diversas áreas, como arquitetura, engenharia e design.A principal diferença entre retângulos e quadrados reside em seus ângulos e lados.
Enquanto os retângulos possuem quatro ângulos retos e lados opostos iguais, os quadrados, além de possuírem quatro ângulos retos, também têm todos os quatro lados iguais. Essa simetria adicional no quadrado gera propriedades únicas que impactam os cálculos geométricos.
Características dos Quadriláteros
Para entender as diferenças, é crucial estabelecer as características fundamentais de ambos os quadriláteros. A distinção entre seus lados e ângulos define suas propriedades geométricas.
- Retângulo: Um retângulo é um quadrilátero com quatro ângulos retos e lados opostos iguais. Isso significa que os lados opostos são paralelos e congruentes, e os ângulos internos são todos iguais a 90 graus. A relação entre os lados não determina necessariamente a igualdade entre eles, podendo ser diferentes.
- Quadrado: Um quadrado é um quadrilátero com quatro ângulos retos e quatro lados congruentes (iguais). Essa característica fundamental o diferencia dos retângulos, tornando-o um caso especial de retângulo com lados iguais. A igualdade dos lados resulta em propriedades adicionais, como a simetria perfeita em torno de seus centros.
Comparativo entre Retângulo e Quadrado
A tabela a seguir resume as diferenças entre retângulos e quadrados, destacando as propriedades essenciais de cada um.
| Característica | Retângulo | Quadrado |
|---|---|---|
| Ângulos | Quatro ângulos retos (90°) | Quatro ângulos retos (90°) |
| Lados | Lados opostos iguais e paralelos | Quatro lados iguais e paralelos |
| Diagonais | Diagonais iguais | Diagonais iguais e perpendiculares |
| Simetria | Simetria em relação a dois eixos | Simetria em relação a dois eixos e em relação ao centro |
Importância das Diferenças, Diferença entre calcular a diagonal de um retângulo e um quadrado.
Compreender as diferenças entre retângulos e quadrados é crucial para aplicar as fórmulas corretas para o cálculo da diagonal. Em problemas práticos, como calcular a área de um terreno retangular ou a medida de uma diagonal de uma placa quadrada, a identificação precisa do tipo de quadrilátero é essencial para obter resultados precisos. A diferença entre lados iguais e lados opostos iguais influencia diretamente no cálculo da diagonal, refletindo a relação entre os lados e os ângulos de cada figura.
Exercícios e Problemas
A prática consistente é fundamental para a consolidação do aprendizado. Os exercícios propostos a seguir visam aprimorar a compreensão e a aplicação dos conceitos relacionados ao cálculo da diagonal de retângulos e quadrados, utilizando o Teorema de Pitágoras como ferramenta principal.Os exercícios abrangem diferentes níveis de complexidade, desde situações mais diretas até problemas que exigem raciocínio lógico e a aplicação de fórmulas.
A resolução detalhada de cada exercício, incluindo as etapas intermediárias, contribui para a assimilação dos métodos de cálculo e para a identificação de possíveis erros.
Cálculo da Diagonal de Retângulos
Para calcular a diagonal de um retângulo, aplica-se o Teorema de Pitágoras, considerando os lados do retângulo como catetos e a diagonal como a hipotenusa.
- Exercício 1: Determine a diagonal de um retângulo com lados medindo 6 cm e 8 cm. Apresente as etapas de resolução.
Solução: Utilizando o Teorema de Pitágoras (a² + b² = c²), onde ‘a’ e ‘b’ são os lados do retângulo e ‘c’ é a diagonal. Substituindo os valores, temos: 6² + 8² = c². Calculando, 36 + 64 = c², resultando em 100 = c². A diagonal ‘c’ é igual a √100, ou seja, 10 cm.
- Exercício 2: Um retângulo possui uma diagonal medindo 15 cm e um lado com 9 cm. Qual o comprimento do outro lado? Mostre os passos.
Solução: Aplicando o Teorema de Pitágoras: a² + b² = c². Sabemos que c = 15 e a = 9. Portanto, 9² + b² = 15². Calculando, 81 + b² = 225. Isolando b², temos b² = 225 – 81, o que resulta em b² = 144.
Extraindo a raiz quadrada, b = √144, ou seja, 12 cm.
Cálculo da Diagonal de Quadrados
A diagonal de um quadrado pode ser calculada utilizando uma fórmula simplificada, derivada do Teorema de Pitágoras.
- Exercício 3: Um quadrado possui lado medindo 5 cm. Qual o comprimento de sua diagonal? Apresente as etapas.
Solução: A fórmula para a diagonal de um quadrado é: diagonal = lado
– √
2. Substituindo o valor do lado (5 cm), temos: diagonal = 5 cm
– √2. A diagonal mede aproximadamente 7,07 cm.
- Exercício 4: A diagonal de um quadrado mede 10 cm. Qual o comprimento do seu lado? Mostre as etapas.
Solução: Utilizando a fórmula diagonal = lado
– √2, temos: 10 cm = lado
– √2. Isolando o lado, lado = 10 cm / √2. Simplificando, o lado mede aproximadamente 7,07 cm.
Problemas de Aplicação
- Exercício 5: Uma placa retangular de 12 cm de largura e 16 cm de comprimento deve ser colocada em uma caixa. Qual o menor comprimento que a caixa deve ter para acomodar a placa diagonalmente? Detalhe os passos.
Solução: A diagonal da placa representa a hipotenusa do triângulo retângulo formado pelos lados da placa. Utilizando o Teorema de Pitágoras, 12² + 16² = diagonal². Calculando, 144 + 256 = diagonal², o que resulta em 400 = diagonal². A diagonal mede √400 = 20 cm. Portanto, o comprimento mínimo da caixa deve ser de 20 cm.
Em resumo, calcular a diagonal de um retângulo e de um quadrado envolve aplicações distintas do Teorema de Pitágoras. Enquanto a fórmula para o retângulo considera dois lados diferentes, a do quadrado emprega apenas um lado. Compreender essas diferenças permite a aplicação adequada das fórmulas e a resolução de problemas geométricos com precisão. Este estudo proporcionou uma análise detalhada das fórmulas e exemplos, demonstrando como os lados influenciam o comprimento da diagonal.
Qual a fórmula geral para calcular a diagonal de um quadrilátero?
Não existe uma fórmula única para todos os quadriláteros. A fórmula depende do tipo de quadrilátero (retângulo, quadrado, paralelogramo, etc.) e é baseada em propriedades específicas.
Como o Teorema de Pitágoras é aplicado no cálculo da diagonal de um retângulo?
O Teorema de Pitágoras é utilizado para relacionar os lados e a diagonal de um retângulo, formando um triângulo retângulo com a diagonal como hipotenusa.
Existe alguma diferença prática entre calcular a diagonal de um retângulo e de um quadrado?
Sim, a diferença está na simplicidade da fórmula para o quadrado, pois todos os seus lados são iguais. No retângulo, a fórmula envolve os dois lados distintos.





